Procesos Gaussianos en estructuras de datos discretos

Este ejemplo ilustra el uso de procesos gaussianos para tareas de regresión y clasificación en datos que no están en forma de vector de características de longitud fija. Esto se consigue mediante el uso de funciones núcleo que operan directamente sobre estructuras discretas como secuencias de longitud variable, árboles y gráficos.

En concreto, aquí las variables de entrada son algunas secuencias de genes almacenadas como cadenas de longitud variable compuestas por letras «A», «T», «C» y «G», mientras que las variables de salida son números de punto flotante y etiquetas True/False en las tareas de regresión y clasificación, respectivamente.

Un núcleo entre las secuencias del gen se define usando R-convolution 1 integrando un núcleo binario en sentido de las letras sobre todos los pares de letras entre un par de cadenas.

Este ejemplo generará tres cifras.

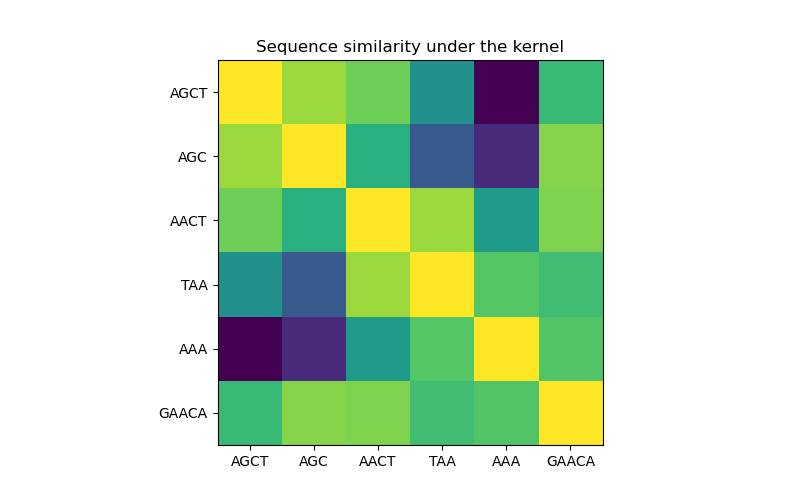
En la primera figura, visualizamos el valor del núcleo, p.ej. la similitud de las secuencias, usando un mapa de color, el color brillante aquí indica una mayor similitud.

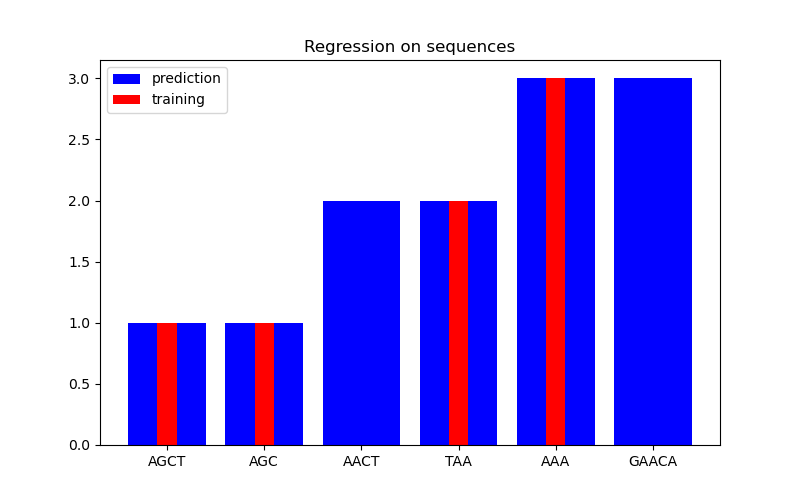
En la segunda figura, mostramos algún resultado de regresión en un conjunto de datos de 6 secuencias. Aquí utilizamos las 1ra, 2da, 4ta y 5ta secuencias como entrenamiento para hacer predicciones sobre las secuencias 3ra y 6ta.

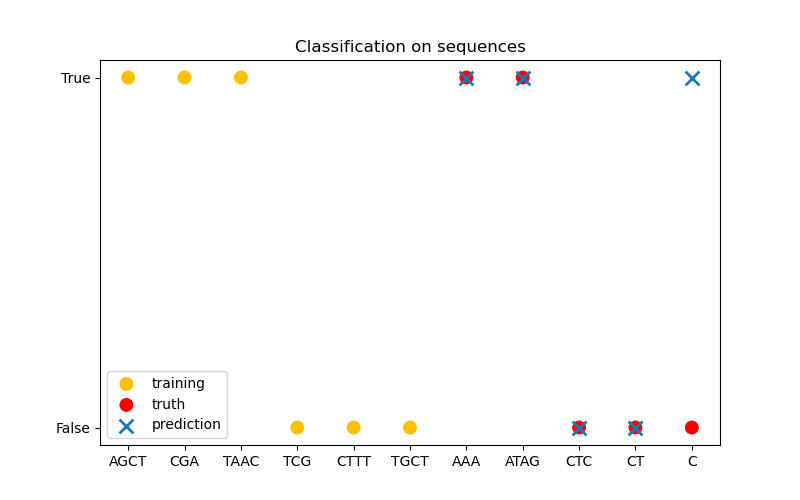
En la tercera figura, demostramos un modelo de clasificación entrenando en 6 secuencias y haciendo predicciones en otras 5 secuencias. La verdad básica aquí es simplemente si hay al menos una «A» en la secuencia. Aquí el modelo hace cuatro clasificaciones correctas y falla en una.

1

Haussler, D. (1999). Convolution kernels on discrete structures (Vol. 646). Technical report, Department of Computer Science, University of California at Santa Cruz.

• 
• 
• 

Out:

/home/mapologo/miniconda3/envs/sklearn/lib/python3.9/site-packages/scikit_learn-0.24.1-py3.9-linux-x86_64.egg/sklearn/gaussian_process/kernels.py:402: ConvergenceWarning: The optimal value found for dimension 0 of parameter baseline_similarity is close to the specified lower bound 1e-05. Decreasing the bound and calling fit again may find a better value.
  warnings.warn("The optimal value found for "

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process.kernels import Kernel, Hyperparameter
from sklearn.gaussian_process.kernels import GenericKernelMixin
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.base import clone


class SequenceKernel(GenericKernelMixin, Kernel):
    '''
    A minimal (but valid) convolutional kernel for sequences of variable
    lengths.'''
    def __init__(self,
                 baseline_similarity=0.5,
                 baseline_similarity_bounds=(1e-5, 1)):
        self.baseline_similarity = baseline_similarity
        self.baseline_similarity_bounds = baseline_similarity_bounds

    @property
    def hyperparameter_baseline_similarity(self):
        return Hyperparameter("baseline_similarity",
                              "numeric",
                              self.baseline_similarity_bounds)

    def _f(self, s1, s2):
        '''
        kernel value between a pair of sequences
        '''
        return sum([1.0 if c1 == c2 else self.baseline_similarity
                   for c1 in s1
                   for c2 in s2])

    def _g(self, s1, s2):
        '''
        kernel derivative between a pair of sequences
        '''
        return sum([0.0 if c1 == c2 else 1.0
                    for c1 in s1
                    for c2 in s2])

    def __call__(self, X, Y=None, eval_gradient=False):
        if Y is None:
            Y = X

        if eval_gradient:
            return (np.array([[self._f(x, y) for y in Y] for x in X]),
                    np.array([[[self._g(x, y)] for y in Y] for x in X]))
        else:
            return np.array([[self._f(x, y) for y in Y] for x in X])

    def diag(self, X):
        return np.array([self._f(x, x) for x in X])

    def is_stationary(self):
        return False

    def clone_with_theta(self, theta):
        cloned = clone(self)
        cloned.theta = theta
        return cloned


kernel = SequenceKernel()

'''
Sequence similarity matrix under the kernel
===========================================
'''

X = np.array(['AGCT', 'AGC', 'AACT', 'TAA', 'AAA', 'GAACA'])

K = kernel(X)
D = kernel.diag(X)

plt.figure(figsize=(8, 5))
plt.imshow(np.diag(D**-0.5).dot(K).dot(np.diag(D**-0.5)))
plt.xticks(np.arange(len(X)), X)
plt.yticks(np.arange(len(X)), X)
plt.title('Sequence similarity under the kernel')

'''
Regression
==========
'''

X = np.array(['AGCT', 'AGC', 'AACT', 'TAA', 'AAA', 'GAACA'])
Y = np.array([1.0, 1.0, 2.0, 2.0, 3.0, 3.0])

training_idx = [0, 1, 3, 4]
gp = GaussianProcessRegressor(kernel=kernel)
gp.fit(X[training_idx], Y[training_idx])

plt.figure(figsize=(8, 5))
plt.bar(np.arange(len(X)), gp.predict(X), color='b', label='prediction')
plt.bar(training_idx, Y[training_idx], width=0.2, color='r',
        alpha=1, label='training')
plt.xticks(np.arange(len(X)), X)
plt.title('Regression on sequences')
plt.legend()

'''
Classification
==============
'''

X_train = np.array(['AGCT', 'CGA', 'TAAC', 'TCG', 'CTTT', 'TGCT'])
# whether there are 'A's in the sequence
Y_train = np.array([True, True, True, False, False, False])

gp = GaussianProcessClassifier(kernel)
gp.fit(X_train, Y_train)

X_test = ['AAA', 'ATAG', 'CTC', 'CT', 'C']
Y_test = [True, True, False, False, False]

plt.figure(figsize=(8, 5))
plt.scatter(np.arange(len(X_train)), [1.0 if c else -1.0 for c in Y_train],
            s=100, marker='o', edgecolor='none', facecolor=(1, 0.75, 0),
            label='training')
plt.scatter(len(X_train) + np.arange(len(X_test)),
            [1.0 if c else -1.0 for c in Y_test],
            s=100, marker='o', edgecolor='none', facecolor='r', label='truth')
plt.scatter(len(X_train) + np.arange(len(X_test)),
            [1.0 if c else -1.0 for c in gp.predict(X_test)],
            s=100, marker='x', edgecolor=(0, 1.0, 0.3), linewidth=2,
            label='prediction')
plt.xticks(np.arange(len(X_train) + len(X_test)),
           np.concatenate((X_train, X_test)))
plt.yticks([-1, 1], [False, True])
plt.title('Classification on sequences')
plt.legend()

plt.show()