Predicciones probabilistas con clasificación de procesos Gaussianos (GPC)

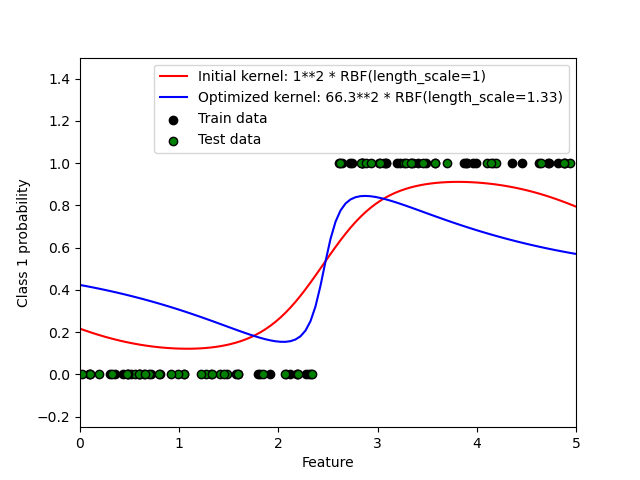
Este ejemplo ilustra la probabilidad pronosticada de GPC para un núcleo RBF con diferentes elecciones de los hiperparámetros. La primera figura muestra la probabilidad predicha de GPC con hiperparámetros elegidos arbitrariamente y con los hiperparámetros correspondientes a la máxima verosimilitud marginal logarítmica (LML).

Aunque los hiperparámetros elegidos mediante la optimización de LML tienen un LML considerablemente mayor, su rendimiento es ligeramente inferior de acuerdo con la pérdida logarítmica en los datos de prueba. La figura muestra que esto se debe a que exhiben un cambio pronunciado de las probabilidades de clase en los límites de la clase (lo cual es bueno) pero tienen probabilidades predichas cercanas a 0,5 lejos de los límites de la clase (lo cual es malo) Este efecto indeseable es causado por la aproximación de Laplace utilizada internamente por GPC.

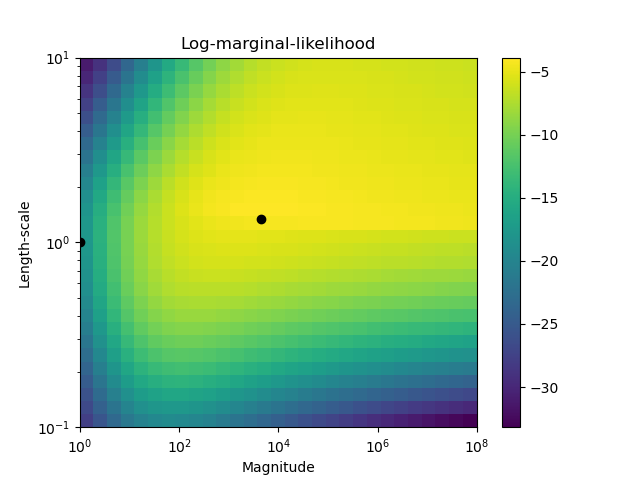
La segunda figura muestra la verosimilitud marginal logarítmica para diferentes opciones de los hiperparámetros del núcleo, destacando las dos opciones de los hiperparámetros utilizados en la primera figura mediante puntos negros.

• 
• 

Out:

Log Marginal Likelihood (initial): -17.598
Log Marginal Likelihood (optimized): -3.875
Accuracy: 1.000 (initial) 1.000 (optimized)
Log-loss: 0.214 (initial) 0.319 (optimized)
/home/mapologo/Descargas/scikit-learn-0.24.X/examples/gaussian_process/plot_gpc.py:94: MatplotlibDeprecationWarning: shading='flat' when X and Y have the same dimensions as C is deprecated since 3.3.  Either specify the corners of the quadrilaterals with X and Y, or pass shading='auto', 'nearest' or 'gouraud', or set rcParams['pcolor.shading'].  This will become an error two minor releases later.
  plt.pcolor(Theta0, Theta1, LML)

print(__doc__)

# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
#
# License: BSD 3 clause

import numpy as np

from matplotlib import pyplot as plt

from sklearn.metrics import accuracy_score, log_loss
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF


# Generate data
train_size = 50
rng = np.random.RandomState(0)
X = rng.uniform(0, 5, 100)[:, np.newaxis]
y = np.array(X[:, 0] > 2.5, dtype=int)

# Specify Gaussian Processes with fixed and optimized hyperparameters
gp_fix = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0),
                                   optimizer=None)
gp_fix.fit(X[:train_size], y[:train_size])

gp_opt = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0))
gp_opt.fit(X[:train_size], y[:train_size])

print("Log Marginal Likelihood (initial): %.3f"
      % gp_fix.log_marginal_likelihood(gp_fix.kernel_.theta))
print("Log Marginal Likelihood (optimized): %.3f"
      % gp_opt.log_marginal_likelihood(gp_opt.kernel_.theta))

print("Accuracy: %.3f (initial) %.3f (optimized)"
      % (accuracy_score(y[:train_size], gp_fix.predict(X[:train_size])),
         accuracy_score(y[:train_size], gp_opt.predict(X[:train_size]))))
print("Log-loss: %.3f (initial) %.3f (optimized)"
      % (log_loss(y[:train_size], gp_fix.predict_proba(X[:train_size])[:, 1]),
         log_loss(y[:train_size], gp_opt.predict_proba(X[:train_size])[:, 1])))


# Plot posteriors
plt.figure()
plt.scatter(X[:train_size, 0], y[:train_size], c='k', label="Train data",
            edgecolors=(0, 0, 0))
plt.scatter(X[train_size:, 0], y[train_size:], c='g', label="Test data",
            edgecolors=(0, 0, 0))
X_ = np.linspace(0, 5, 100)
plt.plot(X_, gp_fix.predict_proba(X_[:, np.newaxis])[:, 1], 'r',
         label="Initial kernel: %s" % gp_fix.kernel_)
plt.plot(X_, gp_opt.predict_proba(X_[:, np.newaxis])[:, 1], 'b',
         label="Optimized kernel: %s" % gp_opt.kernel_)
plt.xlabel("Feature")
plt.ylabel("Class 1 probability")
plt.xlim(0, 5)
plt.ylim(-0.25, 1.5)
plt.legend(loc="best")

# Plot LML landscape
plt.figure()
theta0 = np.logspace(0, 8, 30)
theta1 = np.logspace(-1, 1, 29)
Theta0, Theta1 = np.meshgrid(theta0, theta1)
LML = [[gp_opt.log_marginal_likelihood(np.log([Theta0[i, j], Theta1[i, j]]))
        for i in range(Theta0.shape[0])] for j in range(Theta0.shape[1])]
LML = np.array(LML).T
plt.plot(np.exp(gp_fix.kernel_.theta)[0], np.exp(gp_fix.kernel_.theta)[1],
         'ko', zorder=10)
plt.plot(np.exp(gp_opt.kernel_.theta)[0], np.exp(gp_opt.kernel_.theta)[1],
         'ko', zorder=10)
plt.pcolor(Theta0, Theta1, LML)
plt.xscale("log")
plt.yscale("log")
plt.colorbar()
plt.xlabel("Magnitude")
plt.ylabel("Length-scale")
plt.title("Log-marginal-likelihood")

plt.show()