1.8. Descomposición cruzada¶
El módulo de descomposición cruzada contiene estimadores supervisados para la reducción de la dimensionalidad y la regresión, pertenecientes a la familia de los «mínimos cuadrados parciales».
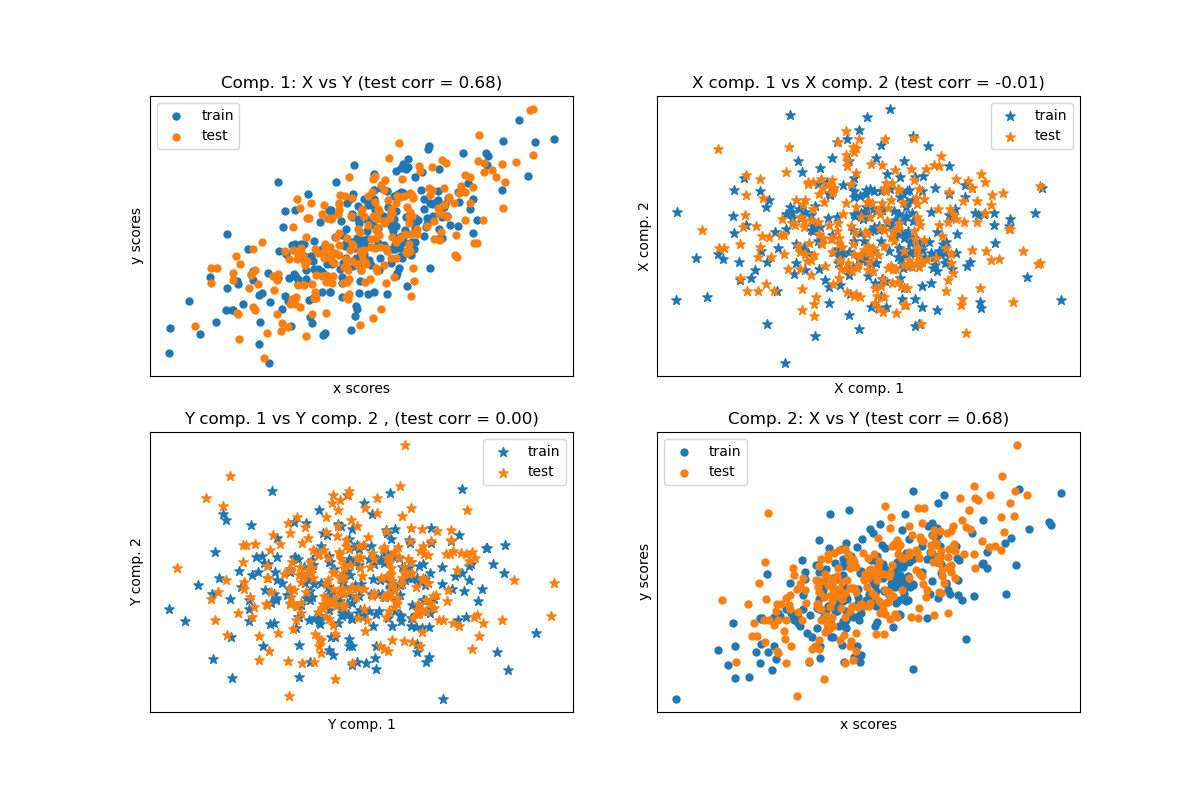
Los algoritmos de descomposición cruzada encuentran las relaciones fundamentales entre dos matrices (X e Y). Son enfoques de variables latentes para modelar las estructuras de covarianza en estos dos espacios. Tratan de encontrar la dirección multidimensional en el espacio X que explica la máxima dirección de varianza multidimensional en el espacio Y. En otras palabras, PLS proyecta tanto X como Y en un subespacio de menor dimensión tal que la covarianza entre transformada(X) y transformada(Y) es máxima.
El PLS guarda similitudes con la «Regresión de Componentes Principales» (PCR), en la que las muestras se proyectan primero en un subespacio de menor dimensión y los objetivos y se predicen utilizando transformed(X). Uno de los problemas de la PCR es que la reducción de la dimensionalidad no está supervisada y puede ignorar algunas variables importantes: La PCR mantendría las características con la mayor varianza, pero es posible que las características con una pequeña varianza sean relevantes para predecir el resultado. En cierto modo, PLS permite el mismo tipo de reducción de la dimensionalidad, pero teniendo en cuenta los objetivos y. El siguiente ejemplo ilustra este hecho: * Regresión por componentes principales frente a la regresión por mínimos cuadrados parciales.
Aparte de CCA, los estimadores PLS son especialmente adecuados cuando la matriz de predictores tiene más variables que observaciones, y cuando hay multicolinealidad entre las características. Por el contrario, la regresión lineal estándar fracasaría en estos casos a menos que sea regularizada.
Las clases incluidas en este módulo son PLSRegression, PLSCanonical, CCA and PLSVD
1.8.1. PLSCanonical¶
Aquí describimos el algoritmo usado en PLSCanonical. Los otros estimadores usan variantes de este algoritmo, y se detallan a continuación. Recomendamos la sección 1 para más detalles y comparaciones entre estos algoritmos. En 1, PLSCanonical corresponde a «PLSW2A».
Dadas dos matrices centradas \(X \in \mathbb{R}^{n \times d}\) y \(Y \in \mathbb{R}^{n \times t}\), y un número de componentes \(K\), PLSCanonical prosigue como se indica a continuación:
Defina \(X_1\) como \(X\) y \(Y_1\) como \(Y\). Entonces, para cada \(k \in [1, K]\):
a) compute \(u_k \in \mathbb{R}^d\) and \(v_k \in \mathbb{R}^t\), the first left and right singular vectors of the cross-covariance matrix \(C = X_k^T Y_k\). \(u_k\) and \(v_k\) are called the weights. By definition, \(u_k\) and \(v_k\) are choosen so that they maximize the covariance between the projected \(X_k\) and the projected target, that is \(\text{Cov}(X_k u_k, Y_k v_k)\).
b) Project \(X_k\) and \(Y_k\) on the singular vectors to obtain scores: \(\xi_k = X_k u_k\) and \(\omega_k = Y_k v_k\)
c) Regress \(X_k\) on \(\xi_k\), i.e. find a vector \(\gamma_k \in \mathbb{R}^d\) such that the rank-1 matrix \(\xi_k \gamma_k^T\) is as close as possible to \(X_k\). Do the same on \(Y_k\) with \(\omega_k\) to obtain \(\delta_k\). The vectors \(\gamma_k\) and \(\delta_k\) are called the loadings.
d) deflate \(X_k\) and \(Y_k\), i.e. subtract the rank-1 approximations: \(X_{k+1} = X_k - \xi_k \gamma_k^T\), and \(Y_{k + 1} = Y_k - \omega_k \delta_k^T\).
Al final, hemos aproximado \(X\) como una suma de matrices de rango 1: \(X = \Xi \Gamma^T\) donde \(\Xi \in \mathbb{R}^{n \times K}\) contiene las puntuaciones en sus columnas, y \(\Gamma^T \in \mathbb{R}^{K \times d}\) contiene las cargas en sus filas. Del mismo modo, para \(Y\), tenemos \(Y = \Omega \Delta^T\).
Observa que las matrices de puntuación \(\Xi\) y \(Omega\) corresponden a las proyecciones de los datos de entrenamiento \(X\) y \(Y\), respectivamente.
El paso a) puede realizarse de dos maneras: calculando toda la SVD de \(C\) y conservando sólo los vectores singulares con los mayores valores singulares, o calculando directamente los vectores singulares utilizando el método de la potencia (cf. sección 11.3 en 1), que corresponde a la opción 'nipals del parámetro algorithm.
1.8.1.1. Transformación de datos¶
Para transformar \(X\) en \(\bar{X}\), necesitamos encontrar una matriz de proyección \(P\) tal que \(bar{X} = XP\). Sabemos que para los datos de entrenamiento, \(\Xi = XP\), y \(X = \Xi \Gamma^T\). Estableciendo \(P = U(\Gamma^T U)^{-1}\) donde \(U\) es la matriz con los \(u_k\) en las columnas, tenemos \(XP = X U(\Gamma^T U)^{-1} = \Xi (\Gamma^T U) (\Gamma^T U)^{-1} = \Xi\) tal y como se quiere. Se puede acceder a la matriz de rotación \(P\) desde el atributo x_rotations_.
Del mismo modo, \(Y\) puede ser transformada usando la matriz de rotación \(V(\Delta^T V)^{-1}\), a lo que se tiene acceso a través del atributo y_rotations_.
1.8.1.2. Predicción de los objetivos Y¶
Para predecir los objetivos de algunos datos \(X\), estamos buscando una matriz de coeficiente \(\beta \in R^{d \times t}\) tal que \(Y = X\beta\).
La idea es tratar de predecir los objetivos transformados \(\Omega\) como una función de las muestras transformadas \(\Xi\), calculando \(\alpha \in \mathbb{R}\) tal que \(\Omega = \alpha \Xi\).
Luego, tenemos \(Y = \Omega \Delta^T = \alpha \Xi \Delta^T\), y ya que \(\Xi\) son los datos de entrenamiento transformados, tenemos que \(Y = X \alpha P \Delta^T\), y como resultado la matriz de coeficiente \(\beta = \alpha P \Delta^T\).
\(\beta\) puede ser accedido mediante el atributo coef_.
1.8.2. PLSSVD¶
PLSSVD es una versión simplificada de PLSCanonical descrita anteriormente: en lugar de disminuir iterativamente las matrices \(X_k\) y \(Y_k\), PLSSVD calcula la SVD de :math: C = X^TY sólo una vez, y almacena los vectores singulares n_componentes correspondientes a los mayores valores singulares en las matrices U y V, correspondientes a los atributos x_weights_ y y_weights_. Aquí, los datos transformados son simplemente transformed(X) = XU y transformed(Y) = YV.
Si n_components == 1, PLSVD y PLSCanonical son estrictamente equivalentes.
1.8.3. PLSRegression¶
El estimador PLSRegression es similar a PLSCanonical con algorithm='nipals', con 2 diferencias importantes:
en el paso a) del método de potencia para calcular \(u_k\) y \(v_k\), \(v_k\) nunca se normaliza.
en el paso c), los objetivos \(Y_k\) se aproximan utilizando la proyección de \(X_k\) (es decir, \(\xi_k\)) en lugar de la proyección de \(Y_k\) (es decir, \(\omega_k\)). En otras palabras, el cálculo de las cargas es diferente. Como resultado, la disminución en el paso d) también se verá afectada.
Estas dos modificaciones afectan a la salida de predict y transform, que no son las mismas que para PLSCanonical. Además, mientras que el número de componentes está limitado por min(n_samples, n_features, n_targets) en PLSCanonical, aquí el límite es el rango de \(X^TX\), es decir, min(n_samples, n_features).
PLSRegression también se conoce como PLS1 (objetivos simples) y PLS2 (objetivos múltiples). Al igual que Lasso, PLSRegression es una forma de regresión lineal regularizada donde el número de componentes controla la fuerza de la regularización.
1.8.4. Análisis de Correlación Canónica¶
El Análisis de Correlación Canónica se desarrolló previa e independientemente de PLS. Pero resulta que CCA es un caso especial de PLS, y corresponde a PLS en el «Modo B» en la literatura.
CCA difiere de PLSCanonical en la forma en que los pesos \(u_k\) y \(v_k\) son calculados en el método de potencia del paso a). Los detalles se pueden encontrar en la sección 10 de 1.
Como CCA involucra la inversión de \(X_k^TX_k\) y \(Y_k^TY_k\), este estimador puede ser inestable si el número de características o objetivos es mayor que el número de muestras.
Reference:
