1.5. Descenso de Gradiente Estocástico

Descenso de Gradiente Estocástico (Stochastic Gradient Descent, SGD) es un enfoque simple pero muy eficiente para ajustar clasificadores y regresores lineales bajo funciones de pérdida convexas, como las Máquinas de Vectores de Soporte y Regresión Logística (lineales). Aunque el SGD lleva mucho tiempo en la comunidad del aprendizaje automático, ha recibido una atención considerable recientemente en el contexto del aprendizaje a gran escala.

El SGD se ha aplicado con éxito a problemas de aprendizaje automático a gran escala y dispersos, encontrados a menudo en la clasificación de textos y el procesamiento del lenguaje natural. Dado que los datos son dispersos, los clasificadores de este módulo pueden escalar fácilmente a problemas con más de 10^5 ejemplos de entrenamiento y más de 10^5 características.

En sentido estricto, el SGD no es más que una técnica de optimización y no corresponde a una familia específica de modelos de aprendizaje automático. Es sólo una forma de entrenar un modelo. A menudo, una instancia de SGDClassifier o SGDRegressor tendrá un estimador equivalente en la API de scikit-learn, utilizando potencialmente una técnica de optimización diferente. Por ejemplo, el uso de SGDClassifier(loss='log') da como resultado una regresión logística, es decir, un modelo equivalente a LogisticRegression que se ajusta a través de SGD en lugar de ser ajustado por uno de los otros solucionadores en LogisticRegression. Del mismo modo, SGDRegressor(loss='squared_loss', penalty='l2') y Ridge resuelven el mismo problema de optimización, a través de diferentes medios.

Las ventajas del Descenso de Gradiente Estocástico son:

• Eficiencia.

• Facilidad de implementación (muchas oportunidades para el ajuste del código).

Las desventajas del Descenso de Gradiente Estocástico incluyen:

• El SGD requiere una serie de hiperparámetros como el parámetro de regularización y el número de iteraciones.

• El SGD es sensible al escalamiento de características.

Advertencia

Asegúrate de permutar (revolver) tus datos de entrenamiento antes de ajustar el modelo o utiliza shuffle=True para revolver después de cada iteración (utilizado por defecto). También, idealmente, las características deberían ser estandarizadas usando, por ejemplo, make_pipeline(StandardScaler(), SGDClassifier()) (ver Pipelines).

1.5.1. Clasificación

La clase SGDClassifier implementa una rutina de aprendizaje simple de descenso de gradiente estocástico que soporta diferentes funciones de pérdida y penalizaciones para la clasificación. A continuación se muestra la frontera de decisión de un SGDClassifier entrenado con la pérdida de bisagra, equivalente a una SVM lineal.

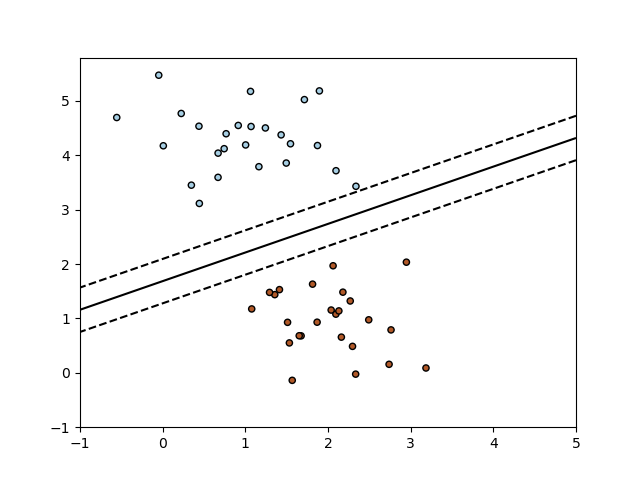
Como otros clasificadores, el SGD tiene que ajustarse con dos arreglos: un arreglo X de forma (n_samples, n_features) que contiene las muestras de entrenamiento, y un arreglo y de forma (n_samples,) que contiene los valores objetivo (etiquetas de clase) para las muestras de entrenamiento:

>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
>>> clf.fit(X, y)
SGDClassifier(max_iter=5)

Una vez ajustado, el modelo puede utilizarse para predecir nuevos valores:

>>> clf.predict([[2., 2.]])
array([1])

SGD ajusta un modelo lineal a los datos de entrenamiento. El atributo coef_ contiene los parámetros del modelo:

>>> clf.coef_
array([[9.9..., 9.9...]])

El atributo intercept_ contiene el intercepto (también conocido como desplazamiento o sesgo):

>>> clf.intercept_
array([-9.9...])

El parámetro fit_intercept controla si el modelo debe utilizar o no un intercepto, es decir, un hiperplano sesgado.

La distancia con signo al hiperplano (calculada como el producto punto entre los coeficientes y la muestra de entrada, más el intercepto) viene dada por SGDClassifier.decision_function:

>>> clf.decision_function([[2., 2.]])
array([29.6...])

La función de pérdida concreta puede establecerse mediante el parámetro loss. SGDClassifier admite las siguientes funciones de pérdida:

• loss="hinge": (margen blando) Máquina de Vectores de Soporte lineal,

• loss="modified_huber": pérdida de bisagra suavizada,

• loss="log": regresión logística,

• y todas las pérdidas de regresión más abajo. En este caso, el objetivo se codifica como -1 o 1, y el problema se trata como un problema de regresión. La clase predicha corresponde entonces al signo del objetivo predicho.

Por favor, consulta la sección matemática más abajo para ver las fórmulas. Las dos primeras funciones de pérdida son perezosas, sólo actualizan los parámetros del modelo si un ejemplo viola la restricción de margen, lo que hace que el entrenamiento sea muy eficiente y puede dar lugar a modelos más dispersos (es decir, con más coeficientes cero), incluso cuando se utiliza la penalización L2.

El uso de loss="log"` o ``loss="modified_huber" habilita el método predict_proba, que da un vector de estimaciones de probabilidad \(P(y|x)\) por muestra \(x\):

>>> clf = SGDClassifier(loss="log", max_iter=5).fit(X, y)
>>> clf.predict_proba([[1., 1.]])
array([[0.00..., 0.99...]])

La penalización concreta puede establecerse mediante el parámetro penalty. SGD admite las siguientes penalizaciones:

• penalty="l2": Penalización de la norma L2 en coef_.

• penalty="l1": Penalización de la norma L1 en coef_.

• penalty="elasticnet": Combinación convexa de L2 y L1; (1 - l1_ratio) * L2 + l1_ratio * L1.

La configuración por defecto es penalty="l2". La penalización L1 conduce a soluciones dispersas, llevando la mayoría de los coeficientes a cero. La Red Elástica 11 resuelve algunas deficiencias de la penalización L1 en presencia de atributos altamente correlacionados. El parámetro l1_ratio controla la combinación convexa de la penalización L1 y L2.

SGDClassifier soporta la clasificación multiclase combinando múltiples clasificadores binarios en un esquema «uno contra todos» (OVA). Para cada una de las clases \(K\), se aprende un clasificador binario que discrimina entre esa y todas las demás clases \(K-1\). En el momento de la prueba, calculamos la puntuación de confianza (es decir, las distancias con signo al hiperplano) de cada clasificador y se elige la clase con mayor confianza. La Figura siguiente ilustra el enfoque OVA en el conjunto de datos del iris. Las líneas discontinuas representan los tres clasificadores OVA; los colores del fondo muestran la superficie de decisión inducida por los tres clasificadores.

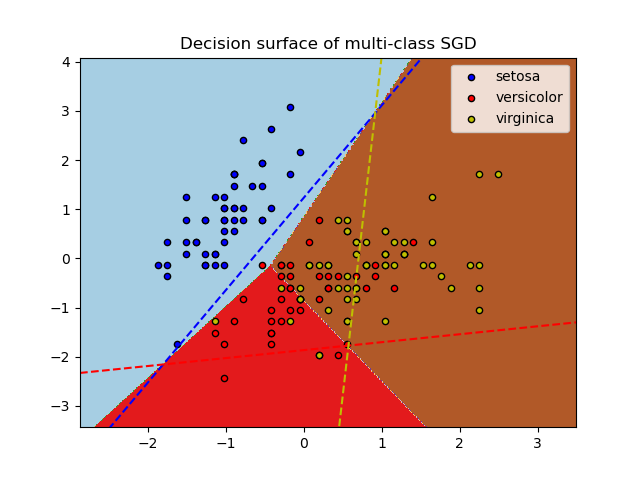
En el caso de la clasificación multiclase, coef_ es un arreglo bidimensional de forma (n_classes, n_features) e intercept_ es un arreglo unidimensional de forma (n_classes,). La fila i-ésima de coef_ contiene el vector de ponderaciones del clasificador OVA para la clase i-ésima; las clases se indexan en orden ascendente (ver el atributo classes_). Ten en cuenta que, en principio, dado que permiten crear un modelo de probabilidad, loss="log" y loss="modified_huber" son más adecuados para la clasificación uno contra todos.

SGDClassifier soporta tanto clases ponderadas como instancias ponderadas a través de los parámetros de ajuste class_weight y sample_weight. Para más información, consulta los ejemplos siguientes y la cadena de documentación de SGDClassifier.fit.

SGDClassifier soporta SGD promediado (averaged SGD, ASGD) 10. El promediado puede activarse estableciendo average=True. ASGD realiza las mismas actualizaciones que el SGD regular (ver Formulación matemática), pero en lugar de utilizar el último valor de los coeficientes como atributo coef_ (es decir, los valores de la última actualización), coef_ se establece en su lugar en el valor promedio de los coeficientes en todas las actualizaciones. Lo mismo se hace con el atributo intercept_. Cuando se utiliza el ASGD, la tasa de aprendizaje puede ser mayor e incluso constante, lo que lleva, en algunos conjuntos de datos, a una aceleración del tiempo de entrenamiento.

Para la clasificación con pérdida logística, otra variante de SGD con una estrategia de promediación está disponible con el algoritmo Gradiente Medio Estocástico (Stochastic Average Gradient , SAG), disponible como un solucionador en LogisticRegression.

Ejemplos:

• SGD: Hiperplano de separación de máximo margen,

• Graficar el SGD multiclase en el conjunto de datos del iris

• SGD: Muestras ponderadas

• Comparación de varios solucionadores en línea

• SVM: Hiperplano de separación para clases desequilibradas (Ver la Nota en el ejemplo)

1.5.2. Regresión

La clase SGDRegressor implementa una rutina de aprendizaje de descenso de gradiente estocástico simple que soporta diferentes funciones de pérdida y penalizaciones para ajustar modelos de regresión lineal. SGDRegressor es muy adecuada para problemas de regresión con un gran número de muestras de entrenamiento (> 10.000), para otros problemas recomendamos Ridge, Lasso, o ElasticNet.

La función de pérdida concreta puede establecerse mediante el parámetro loss. SGDRegressor admite las siguientes funciones de pérdida:

• loss="squared_loss": Mínimos cuadrados ordinarios,

• loss="huber": Pérdida de Huber para una regresión robusta,

• loss="epsilon_insensitive": Regresión de Vectores de Soporte lineal.

Por favor, consulta las fórmulas en la sección matemática más abajo. Las funciones de pérdida Huber e insensibles a épsilon pueden utilizarse para una regresión robusta. La anchura de la región insensible debe especificarse mediante el parámetro epsilon. Este parámetro depende de la escala de las variables objetivo.

El parámetro penalty determina la regularización que se utilizará (ver la descripción anterior en la sección de clasificación).

SGDRegressor también admite el SGD promediado 10 (de nuevo, ver la descripción anterior en la sección de clasificación).

Para la regresión con una pérdida cuadrada y una penalización l2, está disponible otra variante de SGD con una estrategia de promediación con el algoritmo Gradiente Medio Estocástico (Stochastic Average Gradient, SAG), disponible como un solucionador en Ridge.

1.5.3. Descenso de Gradiente Estocástico para datos dispersos

Nota

La implementación dispersa produce resultados ligeramente diferentes de la implementación densa, debido a una tasa de aprendizaje reducida para el intercepto. Ver Detalles de implementación.

Hay soporte integrado para datos dispersos dados en cualquier matriz en un formato soportado por scipy.sparse. Sin embargo, para obtener la máxima eficiencia, utiliza el formato de matriz CSR definido en scipy.sparse.csr_matrix.

Ejemplos:

• Clasificación de documentos de texto utilizando características dispersas

1.5.4. Complejidad

La mayor ventaja de SGD es su eficiencia, que es básicamente lineal en el número de ejemplos de entrenamiento. Si X es una matriz de tamaño (n, p) el entrenamiento tiene un costo de \(O(k n \bar p)\), donde k es el número de iteraciones (épocas) y \(bar p\) es el número promedio de atributos distintos de cero por muestra.

Sin embargo, los resultados teóricos recientes muestran que el tiempo de ejecución para obtener cierta precisión de optimización deseada no aumenta a medida que aumenta el tamaño del conjunto de entrenamiento.

1.5.5. Criterio de parada

Las clases SGDClassifier y SGDRegressor proporcionan dos criterios para detener el algoritmo cuando se alcanza un determinado nivel de convergencia:

• Con early_stopping=True, los datos de entrada se dividen en un conjunto de entrenamiento y un conjunto de validación. El modelo se ajusta al conjunto de entrenamiento y el criterio de parada se basa en la puntuación de la predicción (utilizando el método score) calculada en el conjunto de validación. El tamaño del conjunto de validación puede modificarse con el parámetro validation_fraction.

• Con early_stopping=False, el modelo se ajusta a todos los datos de entrada y el criterio de parada se basa en la función objetivo calculada en los datos de entrenamiento.

En ambos casos, el criterio se evalúa una vez por época, y el algoritmo se detiene cuando el criterio no mejora n_iter_no_change veces seguidas. La mejora se evalúa con la tolerancia absoluta tol, y el algoritmo se detiene en cualquier caso después de un número máximo de iteraciones max_iter.

1.5.6. Consejos de Uso Práctico

• El Descenso de Gradiente Estocástico es sensible al escalamiento de las características, por lo que es muy recomendable escalar tus datos. Por ejemplo, escala cada atributo del vector de entrada X a [0,1] o [-1,+1], o estandarízalo para que tenga media 0 y varianza 1. Ten en cuenta que el mismo escalamiento debe aplicarse al vector de prueba para obtener resultados significativos. Esto puede hacerse fácilmente utilizando StandardScaler:

  from sklearn.preprocessing import StandardScaler
  scaler = StandardScaler()
  scaler.fit(X_train)  # Don't cheat - fit only on training data
  X_train = scaler.transform(X_train)
  X_test = scaler.transform(X_test)  # apply same transformation to test data
  
  # Or better yet: use a pipeline!
  from sklearn.pipeline import make_pipeline
  est = make_pipeline(StandardScaler(), SGDClassifier())
  est.fit(X_train)
  est.predict(X_test)
  

  Si tus atributos tienen una escala intrínseca (por ejemplo, las frecuencias de las palabras o las características de los indicadores) el escalamiento no es necesario.

• La mejor manera de encontrar un término de regularización razonable \(\alpha\) es utilizando la búsqueda automática de hiperparámetros, por ejemplo, GridSearchCV o RandomizedSearchCV, normalmente en el rango 10.0**-np.arange(1,7).

• Empíricamente, encontramos que el SGD converge después de observar aproximadamente 10^6 muestras de entrenamiento. Por tanto, una primera estimación razonable del número de iteraciones es max_iter = np.ceil(10**6 / n), donde n es el tamaño del conjunto de entrenamiento.

• Si se aplica el SGD a las características extraídas mediante el PCA, descubrimos que a menudo es prudente escalar los valores de las características mediante una constante «c» tal que la norma L2 promedio de los datos de entrenamiento sea igual a uno.

• Descubrimos que la SGD Promediada funciona mejor con un mayor número de características y una eta0 más alta

Referencias:

• «Efficient BackProp» Y. LeCun, L. Bottou, G. Orr, K. Müller - In Neural Networks: Tricks of the Trade 1998.

1.5.7. Formulación matemática

Describimos aquí los detalles matemáticos del procedimiento SGD. Un buen resumen con las tasas de convergencia se puede encontrar en 12.

Dado un conjunto de ejemplos de entrenamiento \((x_1, y_1), \ldots, (x_n, y_n)\) donde \(x_i \in \mathbf{R}^m\) y \(y_i \in \mathcal{R}\) (:math: y_i in {-1, 1} para la clasificación), nuestro objetivo es aprender una función de puntuación lineal \(f(x) = w^T x + b\) con parámetros de modelo \(w \in \mathbf{R}^m\) e intercepto \(b \in \mathbf{R}\). Para hacer predicciones para la clasificación binaria, simplemente revisamos el signo de \(f(x)\). Para encontrar los parámetros del modelo, minimizamos el error de entrenamiento regularizado dado por

\[E(w,b) = \frac{1}{n}\sum_{i=1}^{n} L(y_i, f(x_i)) + \alpha R(w)\]

donde \(L\) es una función de pérdida que mide el (des)ajuste del modelo y \(R\) es un término de regularización (también conocido como penalización) que penaliza la complejidad del modelo; \(\alpha > 0\) es un hiperparámetro no negativo que controla la fuerza de la regularización.

Diferentes elecciones de \(L\) implican diferentes clasificadores o regresores:

• Bisagra (margen blando): equivalente a la Clasificación por Vectores de Soporte. \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))\).

• Perceptrón: \(L(y_i, f(x_i)) = \max(0, - y_i f(x_i))\).

• Huber modificado: \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))^2\) si \(y_i f(x_i) > 1\), y \(L(y_i, f(x_i)) = -4 y_i f(x_i)\) en caso contrario.

• Log: equivalente a la Regresión Logística. \(L(y_i, f(x_i)) = \log(1 + \exp (-y_i f(x_i)))\).

• Mínimos cuadrados: Regresión lineal (Ridge o Lasso dependiendo de \(R\)). \(L(y_i, f(x_i)) = \frac{1}{2}(y_i - f(x_i))^2\).

• Huber: menos sensible a los valores atípicos que los mínimos cuadrados. Es equivalente a los mínimos cuadrados cuando \(|y_i - f(x_i)|leq \varepsilon\), y \(L(y_i, f(x_i)) = \varepsilon |y_i - f(x_i)| - \frac{1}{2} \varepsilon^2\) de lo contrario.

• Insensible a épsilon: (margen blando) equivalente a la Regresión de Vectores de Soporte. \(L(y_i, f(x_i)) = \max(0, |y_i - f(x_i)| - \varepsilon)\).

Todas las funciones de pérdida anteriores pueden considerarse como un límite superior del error de clasificación incorrecta (pérdida de cero a uno), como se muestra en la siguiente Figura.

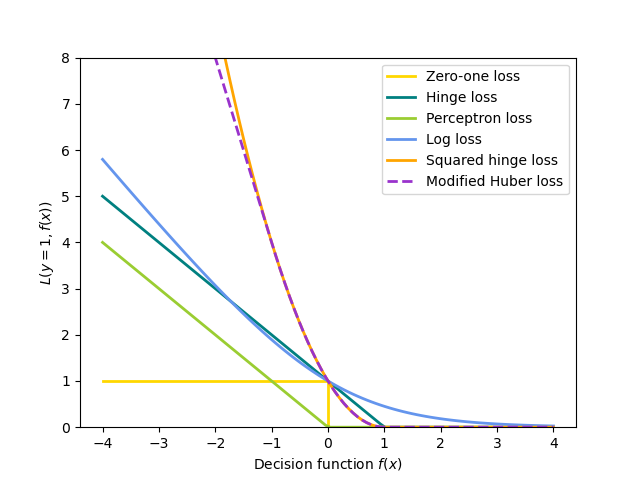
Las opciones populares para el término de regularización \(R\) (el parámetro penalty) incluyen:

• Norma L2: \(R(w) := \frac{1}{2} \sum_{j=1}^{m} w_j^2 = ||w||_2^2\),

• Norma L1: \(R(w) := \sum_{j=1}^{m} |w_j|\), lo que conduce a soluciones dispersas.

• Red elástica: \(R(w) := \frac{\rho}{2} \sum_{j=1}^{n} w_j^2 + (1-\rho) \sum_{j=1}^{m} |w_j|\), una combinación convexa de L2 y L1, donde \(\rho\) viene dado por 1 - l1_ratio.

La Figura siguiente muestra los contornos de los diferentes términos de regularización en un espacio de parámetros bidimensional (\(m=2\)) cuando \(R(w) = 1\).

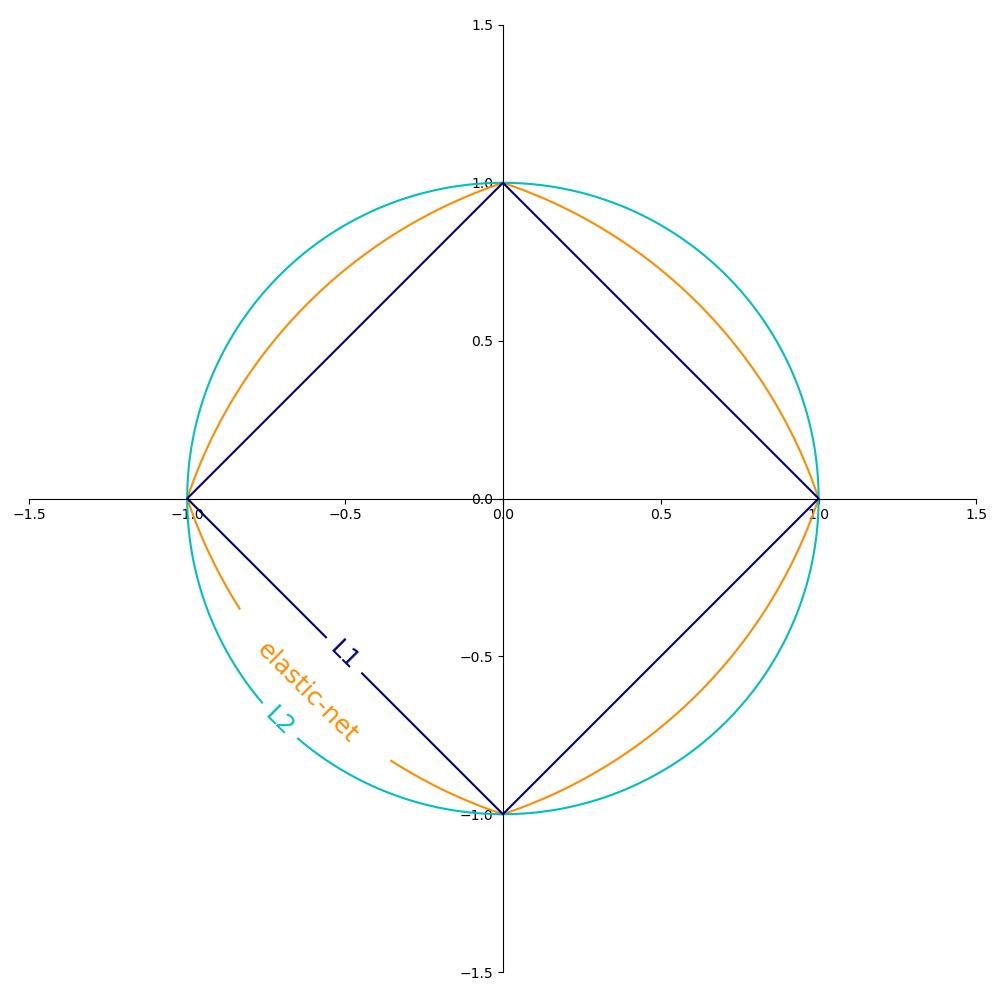
1.5.7.1. SGD

El descenso de gradiente estocástico es un método de optimización para problemas de optimización sin restricciones. A diferencia del descenso de gradiente (por lotes), el SGD se aproxima al verdadero gradiente de \(E(w,b)\) considerando un solo ejemplo de entrenamiento a la vez.

La clase SGDClassifier implementa una rutina de aprendizaje SGD de primer orden. El algoritmo itera sobre los ejemplos de entrenamiento y para cada ejemplo actualiza los parámetros del modelo según la regla de actualización dada por

\[w \leftarrow w - \eta \left[\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial L(w^T x_i + b, y_i)}{\partial w}\right]\]

donde \(\eta\) es la tasa de aprendizaje que controla el tamaño del paso en el espacio de parámetros. El intercepto \(b\) se actualiza de forma similar pero sin regularización (y con un decaimiento adicional para matrices dispersas, como se detalla en Detalles de implementación).

La tasa de aprendizaje \(\eta\) puede ser constante o gradualmente decreciente. Para la clasificación, el programa de tasa de aprendizaje por defecto (learning_rate='optimal') viene dado por

\[\eta^{(t)} = \frac {1}{\alpha (t_0 + t)}\]

donde \(t\) es el paso de tiempo (hay un total de n_samples * n_iter pasos de tiempo), \(t_0\) se determina en base a una heurística propuesta por Léon Bottou de forma que las actualizaciones iniciales esperadas son comparables con el tamaño esperado de las ponderaciones (esto suponiendo que la norma de las muestras de entrenamiento es aproximadamente 1). La definición exacta se puede encontrar en _init_t en BaseSGD.

Para la regresión, el programa de la tasa de aprendizaje por defecto es el escalamiento inverso (learning_rate='invscaling'), dado por

\[\eta^{(t)} = \frac{eta_0}{t^{power\_t}}\]

donde \(eta_0\) y \(power\_t\) son hiperparámetros elegidos por el usuario mediante eta0 y power_t, respectivamente.

Para una tasa de aprendizaje constante, utiliza learning_rate='constant' y utiliza eta0 para especificar la tasa de aprendizaje.

Para una tasa de aprendizaje adaptativamente decreciente, utiliza learning_rate='adaptive' y utiliza eta0 para especificar la tasa de aprendizaje inicial. Cuando se alcanza el criterio de parada, la tasa de aprendizaje es dividida entre 5, y el algoritmo no se detiene. El algoritmo se detiene cuando la tasa de aprendizaje es inferior a 1e-6.

Se puede acceder a los parámetros del modelo a través de los atributos coef_ y intercept_: coef_ contiene las ponderaciones \(w\) e intercept_ contiene \(b\).

Cuando se utiliza el SGD Promediado (con el parámetro average), coef_ se establece en la ponderación promedio de todas las actualizaciones: coef_ \(= \frac{1}{T} \sum_{t=0}^{T-1} w^{(t)}\), donde \(T\) es el número total de actualizaciones, encontradas en el atributo t_.

1.5.8. Detalles de implementación

La implementación de SGD está influenciada por el Stochastic Gradient SVM de 7. De forma similar a SvmSGD, el vector de ponderaciones se representa como el producto de un escalar y un vector que permite una actualización eficiente de las ponderaciones en el caso de la regularización L2. En el caso de una entrada dispersa X, el intercepto se actualiza con una tasa de aprendizaje menor (multiplicada por 0,01) para tener en cuenta el hecho de que se actualiza con mayor frecuencia. Los ejemplos de entrenamiento se recogen secuencialmente y la tasa de aprendizaje se reduce después de cada ejemplo observado. Adoptamos el programa de tasa de aprendizaje de 8. Para la clasificación multiclase, se utiliza un enfoque de «uno contra todos». Utilizamos el algoritmo de gradiente truncado propuesto en 9 para la regularización L1 (y la Red Elástica). El código está escrito en Cython.

Referencias:

7

«Stochastic Gradient Descent» L. Bottou - Website, 2010.

8

«Pegasos: Primal estimated sub-gradient solver for svm» S. Shalev-Shwartz, Y. Singer, N. Srebro - In Proceedings of ICML “07.

9

«Stochastic gradient descent training for l1-regularized log-linear models with cumulative penalty» Y. Tsuruoka, J. Tsujii, S. Ananiadou - In Proceedings of the AFNLP/ACL “09.

10(1,2)

«Towards Optimal One Pass Large Scale Learning with Averaged Stochastic Gradient Descent» Xu, Wei

11

«Regularization and variable selection via the elastic net» H. Zou, T. Hastie - Journal of the Royal Statistical Society Series B, 67 (2), 301-320.

12

«Solving large scale linear prediction problems using stochastic gradient descent algorithms» T. Zhang - In Proceedings of ICML “04.