1.16. Calibración de probabilidad¶
Al realizar la clasificación, a menudo se desea no sólo predecir la etiqueta de la clase, sino también obtener una probabilidad de la etiqueta respectiva. Esta probabilidad le da algún tipo de confianza en la predicción. Algunos modelos pueden dar estimaciones débiles de las probabilidades de clase y algunos incluso no soportan la predicción de probabilidad (por ejemplo, algunas instancias de SGDClassifier). El módulo de calibración le permite calibrar mejor las probabilidades de un modelo dado, o añadir soporte para la predicción de probabilidades.
Los clasificadores bien calibrados son clasificadores probabilísticos para los que la salida del método predict_proba puede interpretarse directamente como un nivel de confianza. Por ejemplo, un clasificador (binario) bien calibrado debería clasificar las muestras de tal manera que entre las muestras a las que dio un valor de predict_proba cercano a 0,8 aproximadamente el 80% pertenecen realmente a la clase positiva.
1.16.1. Curvas de calibración¶
El siguiente gráfico compara qué tan bien se calibran las predicciones probabilísticas de diferentes clasificadores, utilizando calibration_curve. El eje x representa la probabilidad promedio predicha en cada intervalo. El eje y es la fracción de positivos, es decir, la proporción de muestras cuya clase es la positiva (para cada intervalo).
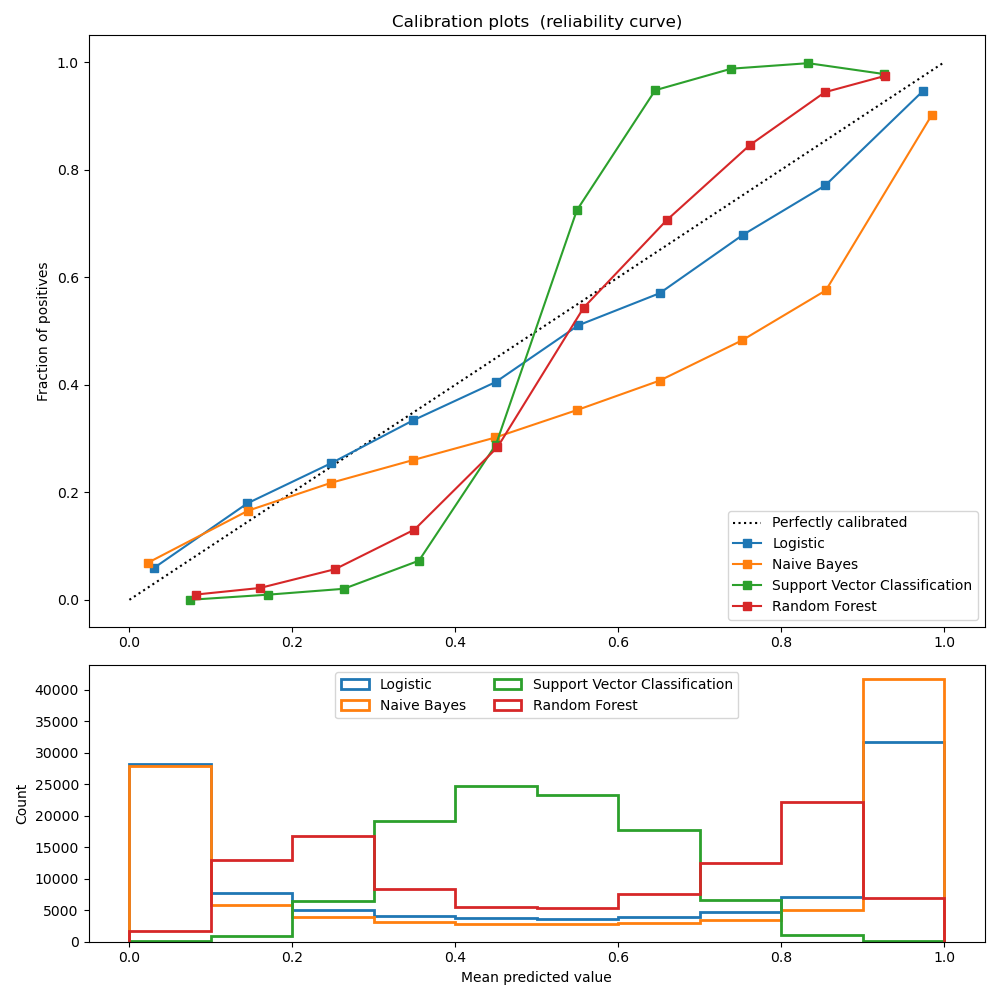
LogisticRegression devuelve predicciones bien calibradas por defecto ya que optimiza directamente Pérdida logística. En cambio, los otros métodos devuelven probabilidades sesgadas; con diferentes sesgos por método:
GaussianNB tiende a llevar las probabilidades a 0 o 1 (observa los recuentos en los histogramas). Esto se debe principalmente a que asume que las características son condicionalmente independientes dada la clase, lo que no es el caso en este conjunto de datos que contiene 2 características redundantes.
RandomForestClassifier muestra el comportamiento opuesto: los histogramas muestran picos con una probabilidad aproximada de 0,2 y 0,9, mientras que las probabilidades cercanas a 0 o 1 son muy poco frecuentes. Niculescu-Mizil y Caruana 1 dan una explicación a esto «Los métodos como el empaquetado (bagging) y los bosques aleatorios que promedian las predicciones de un conjunto de modelos base pueden tener dificultades para hacer predicciones cercanas a 0 y 1 porque la varianza en los modelos base subyacentes sesgará las predicciones que deberían estar cerca de 0 o 1 alejándolos de estos valores. Dado que las predicciones están restringidas al intervalo [0,1], los errores causados por la varianza tienden a ser unilaterales cerca de cero y uno. Por ejemplo, si un modelo debe predecir p = 0 para un caso, la única forma de conseguirlo es que todos los árboles empaquetados predigan cero. Si añadimos ruido a los árboles sobre los que el empaquetado está promediando, este ruido hará que algunos árboles predigan valores mayores que 0 para este caso, alejando así la predicción media del conjunto empaquetado de 0. Observamos este efecto con más fuerza con los bosques aleatorios porque los árboles de nivel base entrenados con bosques aleatorios tienen una varianza relativamente alta debido al subconjunto de características». Como resultado, la curva de calibración, también conocida como diagrama de fiabilidad (Wilks 1995 2), muestra una forma sigmoidea característica, indicando que el clasificador podría confiar más en su «intuición» y devolver probabilidades más cercanas a 0 o 1 típicamente.
La clasificación lineal de vectores de soporte (LinearSVC) muestra una curva aún más sigmoidea que RandomForestClassifier, que es típica de los métodos de margen máximo (compárese con Niculescu-Mizil y Caruana 1), que se centran en las muestras difíciles de clasificar que están cerca de la frontera de decisión (los vectores de soporte).
1.16.2. Calibrar un clasificador¶
Calibrar un clasificador consiste en ajustar un regresor (llamado calibrador) que mapea la salida del clasificador (dada por decision_function o predict_proba) a una probabilidad calibrada en [0, 1]. Al denotar la salida del clasificador para una muestra dada por \(f_i\), el calibrador intenta predecir \(p(y_i = 1 | f_i)\).
Las muestras que se utilizan para ajustar el calibrador no deben ser las mismas que se utilizan para ajustar el clasificador, ya que esto introduciría un sesgo. Esto se debe a que el rendimiento del clasificador en sus datos de entrenamiento sería mejor que en los datos nuevos. Utilizar la salida del clasificador de los datos de entrenamiento para ajustar el calibrador daría como resultado un calibrador sesgado que asigna probabilidades más cercanas a 0 y 1 de lo que debería.
1.16.3. Uso¶
La clase CalibratedClassifierCV es utilizada para calibrar un clasificador.
CalibratedClassifierCV utiliza un enfoque de validación cruzada para asegurar que siempre se utilizan datos no sesgados para ajustar el calibrador. Los datos se dividen en k parejas (train_set, test_set) (determinadas por cv). Cuando ensemble=True (por defecto), el siguiente procedimiento se repite independientemente para cada división de validación cruzada: un clon de base_estimator se entrena primero en el subconjunto de entrenamiento. A continuación, sus predicciones en el subconjunto de prueba se utilizan para ajustar un calibrador (un regresor sigmoide o isotónico). Esto da lugar a un conjunto de k parejas (clasificador, calibrador) donde cada calibrador asigna la salida de su clasificador correspondiente en [0, 1]. Cada pareja se presenta en el atributo calibrated_classifiers_, donde cada entrada es un clasificador calibrado con un método predict_proba que produce probabilidades calibradas. La salida de predict_proba para la instancia principal de CalibratedClassifierCV corresponde a la media de las probabilidades predichas de los k estimadores de la lista calibrated_classifiers_. La salida de predict es la clase que tiene la mayor probabilidad.
Cuando ensemble=False, se utiliza la validación cruzada para obtener predicciones «insesgadas» para todos los datos, mediante cross_val_predict. Estas predicciones insesgadas se utilizan para entrenar el calibrador. El atributo calibrated_classifiers_ consiste en una sola pareja (classifier, calibrator) donde el clasificador es el base_estimator entrenado en todos los datos. En este caso, la salida de predict_proba para CalibratedClassifierCV son las probabilidades predichas obtenidas de la única pareja (classifier, calibrator).
La principal ventaja de ensemble=True es beneficiarse del efecto tradicional de ensamblaje (similar al de Metaestimador de bagging). El conjunto resultante debería estar tanto bien calibrado como ser ligeramente más preciso que con ensemble=False. La principal ventaja de utilizar ensemble=False es computacional: reduce el tiempo total de ajuste al entrenar sólo un clasificador base y un par calibrador, disminuye el tamaño del modelo final y aumenta la velocidad de predicción.
Alternativamente, se puede calibrar un clasificador ya ajustado estableciendo cv="prefit". En este caso, los datos no se dividen y se utilizan todos para ajustar el regresor. Es responsabilidad del usuario asegurarse de que los datos utilizados para ajustar el clasificador son disjuntos de los datos utilizados para ajustar el regresor.
sklearn.metrics.brier_score_loss puede utilizarse para evaluar lo bien que está calibrado un clasificador. Sin embargo, esta métrica debe usarse con cuidado porque una puntuación Brier más baja no siempre significa un modelo mejor calibrado. Esto se debe a que la métrica de la puntuación Brier es una combinación de la pérdida de calibración y la pérdida de refinamiento. La pérdida de calibración se define como la desviación media al cuadrado de las probabilidades empíricas derivadas de la pendiente de los segmentos ROC. La pérdida de refinamiento puede definirse como la pérdida óptima esperada, medida por el área bajo la curva de coste óptimo. Como la pérdida por refinamiento puede cambiar independientemente de la pérdida por calibración, una puntuación Brier más baja no significa necesariamente un modelo mejor calibrado.
CalibratedClassifierCV admite el uso de dos regresores de “calibración”: “sigmoide” e “isotónico”.
1.16.3.1. Sigmoide¶
El regresor sigmoide se basa en el modelo logístico de Platt 3:
donde \(y_i\) es la etiqueta verdadera de la muestra \(i\) y \(f_i\) es la salida del clasificador no calibrado para la muestra \(i\). \(A\) y \(B\) son números reales que se determinan al ajustar el regresor por máxima verosimilitud.
El método sigmoide asume que la curva de calibración puede corregirse aplicando una función sigmoide a las predicciones brutas. Esta suposición se ha justificado empíricamente en el caso de Máquinas de Vectores de Soporte con funciones de núcleo (kernel) comunes en varios conjuntos de datos de referencia en la sección 2.1 de Platt 1999 3 pero no se cumple necesariamente en general. Además, el modelo logístico funciona mejor si el error de calibración es simétrico, lo que significa que la salida del clasificador para cada clase binaria se distribuye normalmente con la misma varianza 6. Esto puede ser un problema para problemas de clasificación muy desequilibrados, en los que los resultados no tienen la misma varianza.
En general, este método es más eficaz cuando el modelo no calibrado está infravalorado (under-confident) y tiene errores de calibración similares tanto para las salidas altas como para las bajas.
1.16.3.2. Isotónico¶
El método “isotónico” ajusta un regresor isotónico no paramétrico, que produce una función escalonada no decreciente (véase sklearn.isotonic). Este método minimiza:
sujeto a \(\hat{f}_i >= \hat{f}_j\) siempre que \(f_i >= f_j\). \(y_i\) sea la etiqueta verdadera de la muestra \(i\) y \(\hat{f}_i\) sea la salida del clasificador calibrado para la muestra \(i\) (es decir, la probabilidad calibrada). Este método es más general en comparación con el “sigmoide”, ya que la única restricción es que la función de mapeo sea monotónicamente creciente. Por tanto, es más potente, ya que puede corregir cualquier distorsión monótona del modelo no calibrado. Sin embargo, es más propenso al sobreajuste, especialmente en conjuntos de datos pequeños 5.
En general, “isotónico” funcionará tan bien o mejor que “sigmoide” cuando haya suficientes datos (más de ~ 1000 muestras) para evitar el sobreajuste 1.
1.16.3.3. Soporte multiclase¶
Tanto los regresores isotónicos como los sigmoides sólo admiten datos unidimensionales (por ejemplo, la salida de una clasificación binaria), pero se amplían para la clasificación multiclase si el estimador base admite predicciones multiclase. Para las predicciones multiclase, CalibratedClassifierCV calibra para cada clase por separado de forma Clasificador One Vs Rest 4. Al predecir las probabilidades, las probabilidades calibradas para cada clase se predicen por separado. Como esas probabilidades no suman necesariamente uno, se realiza un postprocesamiento para normalizarlas.
Ejemplos:
Referencias:
- 1(1,2,3)
Predicting Good Probabilities with Supervised Learning, A. Niculescu-Mizil & R. Caruana, ICML 2005
- 2
On the combination of forecast probabilities for consecutive precipitation periods. Wea. Forecasting, 5, 640–650., Wilks, D. S., 1990a
- 3(1,2)
Probabilistic Outputs for Support Vector Machines and Comparisons to Regularized Likelihood Methods. J. Platt, (1999)
- 4
Transforming Classifier Scores into Accurate Multiclass Probability Estimates. B. Zadrozny & C. Elkan, (KDD 2002)
- 5
Predicting accurate probabilities with a ranking loss. Menon AK, Jiang XJ, Vembu S, Elkan C, Ohno-Machado L. Proc Int Conf Mach Learn. 2012;2012:703-710
- 6
Beyond sigmoids: How to obtain well-calibrated probabilities from binary classifiers with beta calibration Kull, M., Silva Filho, T. M., & Flach, P. (2017).
