1.17. Modelos de redes neuronales (supervisadas)

Advertencia

Esta implementación no está pensada para aplicaciones a gran escala. En particular, scikit-learn no ofrece soporte para GPU. Para implementaciones mucho más rápidas, basadas en la GPU, así como framework que ofrecen mucha más flexibilidad para construir arquitecturas de aprendizaje profundo (deep learning), ver Proyectos Relacionados.

1.17.1. Perceptrón multicapa

El Perceptrón Multicapa (Multi-layer Perceptron, MLP) es un algoritmo de aprendizaje supervisado que aprende una función \(f(\cdot): R^m \rightarrow R^o\) mediante el entrenamiento en un conjunto de datos, donde \(m\) es el número de dimensiones de entrada y \(o\) es el número de dimensiones de la salida. Dado un conjunto de características \(X = {x_1, x_2, ..., x_m}\) y un objetivo \(y\), puede aprender un aproximador de función no lineal para la clasificación o la regresión. Se diferencia de la regresión logística en que, entre la capa de entrada y la de salida, puede haber una o más capas no lineales, llamadas capas ocultas. La figura 1 muestra un MLP de una capa oculta con salida escalar.

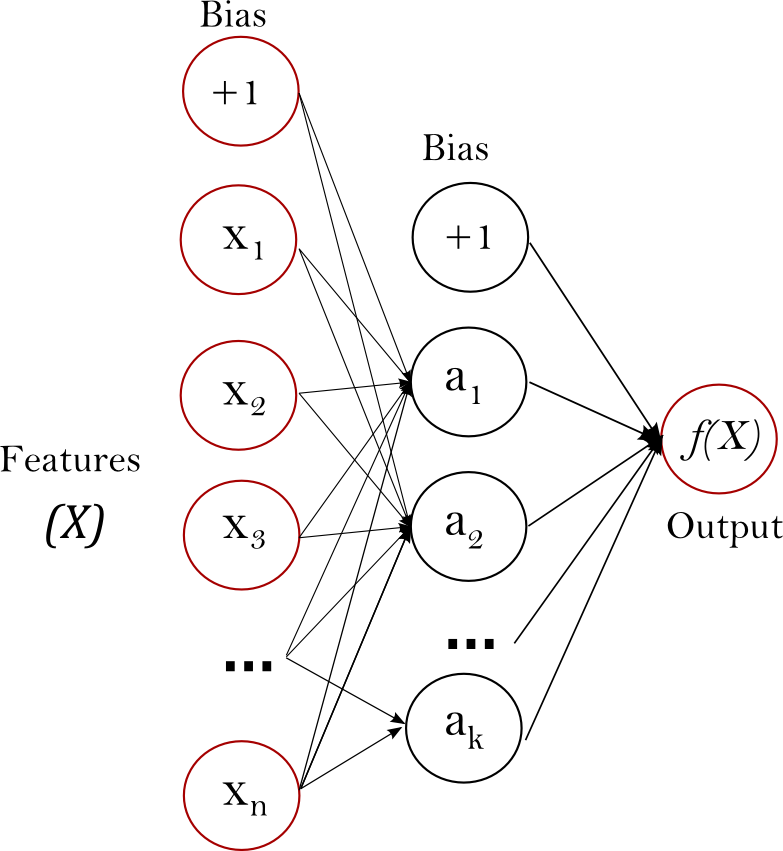
../_images/multilayerperceptron_network.png

Figura 1: MLP de una capa oculta .

La capa más a la izquierda, conocida como la capa de entrada, consiste en un conjunto de neuronas \(\{x_i | x_1, x_2, ..., x_m\}\) que representan las características de entrada. Cada neurona en la capa oculta transforma los valores de la capa anterior con una suma lineal ponderada \(w_1x_1 + w_2x_2 + ... + w_mx_m\), seguida de una función de activación no lineal \(g(\cdot):R \rightarrow R\) - como la función tangente hiperbólica. La capa de salida recibe los valores de la última capa oculta y los transforma en valores de salida.

El módulo contiene los atributos públicos coefs_ y intercepts_. coefs_ es una lista de matrices de pesos, donde la matriz de pesos en el índice \(i\) representa los pesos entre la capa \(i\) y la capa \(i+1\). intercepts_ es una lista de vectores de sesgo, donde el vector en el índice \(i\) representa los valores de sesgo añadidos a la capa \(i+1\).

Las ventajas del Perceptrón Multicapa son:

  • Capacidad para aprender modelos no lineales.

  • Capacidad de aprender modelos en tiempo real (aprendizaje en línea) utilizando partial_fit.

Las desventajas del Perceptrón Multicapa (MLP) incluyen:

  • Los MLP con capas ocultas tienen una función de pérdida no convexa en la que existe más de un mínimo local. Por lo tanto, diferentes inicializaciones de pesos aleatorios pueden conducir a una precisión de validación diferente.

  • Los MLP requieren el ajuste de una serie de hiperparámetros, como el número de neuronas ocultas, las capas y las iteraciones.

  • MLP es sensible al escalamiento de características.

Por favor consulta la sección Consejos de uso práctico que aborda algunas de estas desventajas.

1.17.2. Clasificación

La clase MLPClassifier implementa un algoritmo de perceptrón multicapa (MLP) que se entrena utilizando Retropropagación (Backpropagation).

El MLP se entrena en dos arreglos: el arreglo X de tamaño (n_samples, n_features), que contiene las muestras de entrenamiento representadas como vectores de características de punto flotante; y el arreglo y de tamaño (n_samples,), que contiene los valores objetivo (etiquetas de clase) para las muestras de entrenamiento:

>>> from sklearn.neural_network import MLPClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(5, 2), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(5, 2), random_state=1,
              solver='lbfgs')

Después del ajuste (entrenamiento), el modelo puede predecir las etiquetas para nuevas muestras:

>>> clf.predict([[2., 2.], [-1., -2.]])
array([1, 0])

El MLP puede ajustar un modelo no lineal a los datos de entrenamiento. clf.coefs_ contiene las matrices de pesos que constituyen los parámetros del modelo:

>>> [coef.shape for coef in clf.coefs_]
[(2, 5), (5, 2), (2, 1)]

Actualmente, MLPClassifier sólo admite la función de pérdida Cross-Entropy, que permite estimar la probabilidad ejecutando el método predict_proba.

El MLP se entrena utilizando retropropagación (Backpropagation). Más concretamente, se entrena utilizando alguna forma de descenso de gradiente y los gradientes se calculan utilizando Backpropagation. Para la clasificación, minimiza la función de pérdida de entropía cruzada (Cross-Entropy), dando un vector de estimaciones de probabilidad \(P(y|x)\) por muestra \(x\):

>>> clf.predict_proba([[2., 2.], [1., 2.]])
array([[1.967...e-04, 9.998...-01],
       [1.967...e-04, 9.998...-01]])

MLPClassifier soporta la clasificación multiclase aplicando Softmax como función de salida.

Además, el modelo admite clasificación multi-etiqueta en la que una muestra puede pertenecer a más de una clase. Para cada clase, la salida en bruto pasa por la función logística. Los valores mayores o iguales a 0,5 son redondeados a 1, de lo contrario a 0. Para una salida predicha de una muestra, los índices donde el valor es 1 representan las clases asignadas de esa muestra:

>>> X = [[0., 0.], [1., 1.]]
>>> y = [[0, 1], [1, 1]]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(15,), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(15,), random_state=1,
              solver='lbfgs')
>>> clf.predict([[1., 2.]])
array([[1, 1]])
>>> clf.predict([[0., 0.]])
array([[0, 1]])

Puedes ver los siguientes ejemplos y la cadena de documentación de MLPClassifier.fit para obtener más información.

Ejemplos:

1.17.3. Regresión

La clase MLPRegressor implementa un perceptrón múlticapa (MLP) que se entrena mediante retropropagación (backpropagation) sin función de activación en la capa de salida, lo que también puede ser visto como el uso de la función de identidad como función de activación. Por lo tanto, utiliza el error cuadrado como función de pérdida, y la salida es un conjunto de valores continuos.

MLPRegressor también admite la regresión de salida múltiple, en la que una muestra puede tener más de un objetivo.

1.17.4. Regularización

Tanto MLPRegressor como MLPClassifier utilizan el parámetro alpha para el término regularización (L2 regularization) que ayuda a evitar sobreajuste penalizando pesos con grandes magnitudes. El siguiente gráfico muestra la variación de la función de decisión con el valor de alfa (alpha).

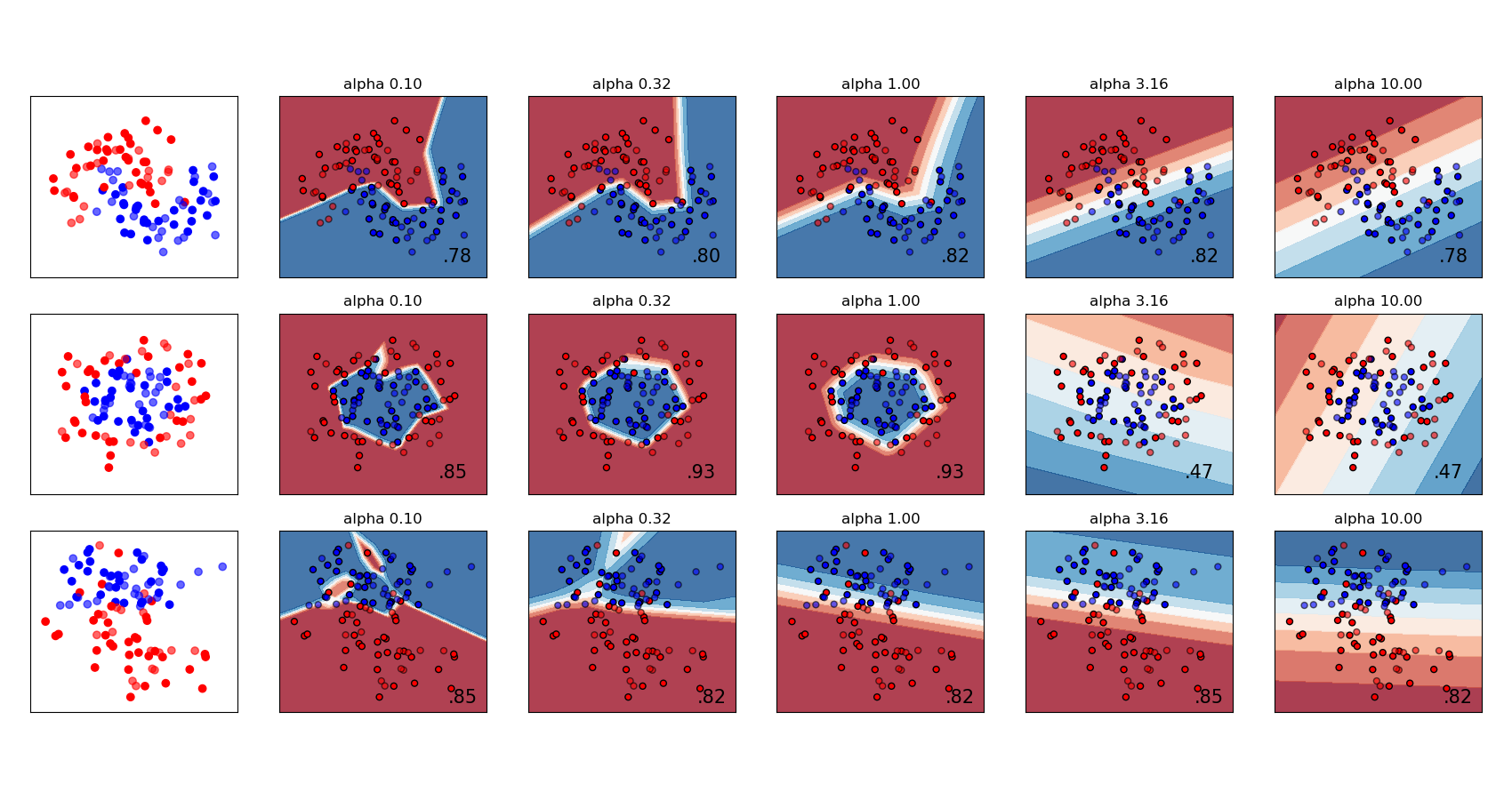
../_images/sphx_glr_plot_mlp_alpha_001.png

Consulta los siguientes ejemplos para obtener más información.

Ejemplos:

1.17.5. Algoritmos

El MPL se entrena utilizando El descenso de gradiente estocástico (Stochastic Gradient Descent), Adam, o L-BFGS. El Descenso Gradiente Estocástico (SGD) actualiza los parámetros utilizando el gradiente de la función de pérdida con respecto a un parámetro que necesita adaptación, es decir.

\[w \leftarrow w - \eta (\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial Loss}{\partial w})\]

donde \(\eta\) es la tasa de aprendizaje que controla el tamaño del paso en la búsqueda del espacio de parámetros. \(Loss\) es la función de pérdida utilizada para la red.

Puedes encontrar más detalles en la documentación de SGD

Adam es similar al SGD en el sentido de que es un optimizador estocástico, pero puede ajustar automáticamente la cantidad para actualizar los parámetros basándose en las estimaciones adaptativas de los momentos de orden inferior.

Con SGD o Adam, el entrenamiento admite aprendizaje en línea y en mini lotes.

L-BFGS es un solucionador que aproxima la matriz Hessiana que representa la derivada parcial de segundo orden de una función. Además, aproxima la inversa de la matriz Hessiana para realizar actualizaciones de parámetros. La implementación utiliza la versión Scipy de L-BFGS.

Si el solucionador seleccionado es “L-BFGS”, el entrenamiento no admite el aprendizaje en línea ni en mini lotes.

1.17.6. Complejidad

Supongamos que hay \(n\) muestras de entrenamiento, \(m\) características, \(k\) capas ocultas, cada una de las cuales contiene \(h\) neuronas - para simplificar, y \(o\) neuronas de salida. La complejidad temporal de la retropropagación es \(O(n\cdot m \cdot h^k \cdot o \cdot i)\), donde \(i\) es el número de iteraciones. Dado que la retropropagación tiene una alta complejidad temporal, es aconsejable empezar con un número menor de neuronas ocultas y pocas capas ocultas para el entrenamiento.

1.17.7. Formulación matemática

Dado un conjunto de ejemplos de entrenamiento \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\) donde \(x_i \in \mathbf{R}^n\) y \(y_i \in \{0, 1\}\), un MLP de una capa oculta y una neurona oculta aprende la función \(f(x) = W_2 g(W_1^T x + b_1) + b_2\) donde \(W_1 \in \mathbf{R}^m\) y \(W_2, b_1, b_2 \in \mathbf{R}\) son parámetros del modelo. \(W_1, W_2\) representan los pesos de la capa de entrada y de la capa oculta, respectivamente; y \(b_1, b_2\) representan el sesgo añadido a la capa oculta y a la capa de salida, respectivamente. \(g(\cdot) : R \rightarrow R\) es la función de activación, establecida por defecto como la tangente hiperbólica. Está dado como,

\[g(z)= \frac{e^z-e^{-z}}{e^z+e^{-z}}\]

Para la clasificación binaria, \(f(x)\) pasa por la función logística \(g(z)=1/(1+e^{-z})\) para obtener valores de salida entre cero y uno. Un umbral, fijado en 0,5, asignaría muestras de salida mayores o iguales 0,5 a la clase positiva, y el resto a la clase negativa.

Si hay más de dos clases, \(f(x)\) sería un vector de tamaño (n_classes,). En lugar de pasar por la función logística, pasa por la función softmax, que se escribe como,

\[\text{softmax}(z)_i = \frac{\exp(z_i)}{\sum_{l=1}^k\exp(z_l)}\]

donde \(z_i\) representa el \(i\) ésimo elemento de la entrada a softmax, que corresponde a la clase \(i\), y \(K\) es el número de clases. El resultado es un vector que contiene las probabilidades de que la muestra \(x\) pertenece a cada clase. La salida es la clase con la mayor probabilidad.

En regresión, la salida permanece como \(f(x)\); por lo tanto, la función de activación de salida es solo la función identidad.

El MLP utiliza diferentes funciones de pérdida dependiendo del tipo de problema. La función de pérdida para la clasificación es la entropía cruzada (Cross-Entropy), que en el caso binario se da como,

\[Loss(\hat{y},y,W) = -y \ln {\hat{y}} - (1-y) \ln{(1-\hat{y})} + \alpha ||W||_2^2\]

donde \(\alpha ||W||_2^2\) es un término de regularización L2 (también conocido como penalización) que penaliza los modelos complejos; y \(\alpha > 0\) es un hiperparámetro no negativo que controla la magnitud de la penalización.

Para la regresión, el MLP utiliza la función de pérdida del Error Cuadrado; escrita como,

\[Loss(\hat{y},y,W) = \frac{1}{2}||\hat{y} - y ||_2^2 + \frac{\alpha}{2} ||W||_2^2\]

A partir de los pesos aleatorios iniciales, el perceptrón multicapa (MLP) minimiza la función de pérdida al actualizar repetidamente estos pesos. Después de calcular la pérdida, un paso hacia atrás la propaga desde la capa de salida a las capas anteriores, proporcionando cada parámetro de peso con un valor de actualización destinado a disminuir la pérdida.

En el descenso del gradiente, el gradiente \(\nabla Loss_{W}\) de la pérdida con respecto a los pesos se calcula y se deduce de \(W\). Más formalmente, esto se expresa como,

\[W^{i+1} = W^i - \epsilon \nabla {Loss}_{W}^{i}\]

donde \(i\) es el paso de iteración, y \(\epsilon\) es la tasa de aprendizaje con un valor mayor que 0.

El algoritmo se detiene cuando alcanza un número máximo preestablecido de iteraciones; o cuando la mejora de la pérdida está por debajo de un número determinado y pequeño.

1.17.8. Consejos de Uso Práctico

  • El Perceptrón Multicapa es sensible al escalamiento de características, por lo que es altamente recomendable escalar los datos. Por ejemplo, escale cada atributo del vector de entrada X a [0, 1] o [-1, +1], o estandarizalo para que tenga una media 0 y una varianza 1. Ten en cuenta que debes aplicar el mismo escalamiento al conjunto de pruebas para obtener resultados significativos. Puedes utilizar StandardScaler para la estandarización.

    >>> from sklearn.preprocessing import StandardScaler  
>>> scaler = StandardScaler()  
>>> # Don't cheat - fit only on training data
>>> scaler.fit(X_train)  
>>> X_train = scaler.transform(X_train)  
>>> # apply same transformation to test data
>>> X_test = scaler.transform(X_test)

    Un enfoque alternativo y recomendado es utilizar StandardScaler en un Pipeline

  • La mejor manera de encontrar un parámetro de regularización razonable \(\alpha\) es utilizar GridSearchCV, normalmente en el rango 10.0 ** -np.arange(1, 7).

  • Empíricamente, observamos que L-BFGS converge más rápido y con mejores soluciones en conjuntos de datos pequeños. Sin embargo, para conjuntos de datos relativamente grandes, Adam es muy robusto. Suele converger rápidamente y ofrece un rendimiento bastante bueno. Por otro lado, SGD con impulso o impulso de Nesterov, puede tener un mejor rendimiento que estos dos algoritmos si la tasa de aprendizaje se ajusta correctamente.

1.17.9. Más control con warm_start

Si quieres tener más control sobre los criterios de parada o la tasa de aprendizaje en SGD, o quieres hacer una supervisión adicional, utiliza warm_start=True y max_iter=1 e iterar tú mismo puede ser útil:

>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(hidden_layer_sizes=(15,), random_state=1, max_iter=1, warm_start=True)
>>> for i in range(10):
...     clf.fit(X, y)
...     # additional monitoring / inspection
MLPClassifier(...

Referencias: