Nota
Haga clic en aquí para descargar el código completo del ejemplo o para ejecutar este ejemplo en su navegador a través de Binder
Calibración de probabilidades para la clasificación de 3 clases¶
Este ejemplo ilustra cómo el sigmoide calibration cambia las probabilidades predichas para un problema de clasificación de 3 clases. Se ilustra el complejo estándar de 2 clases, donde las tres esquinas corresponden a las tres clases. Las flechas apuntan desde los vectores de probabilidad predichos por un clasificador sin calibrar a los vectores de probabilidad predichos por el mismo clasificador después de la calibración sigmoide en un conjunto de validación de retención. Los colores indican la clase verdadera de una instancia (rojo: clase 1, verde: clase 2, azul: clase 3).
Datos¶
A continuación, generamos un conjunto de datos de clasificación con 2000 muestras, 2 características y 3 clases objetivo. A continuación, dividimos los datos de la siguiente manera:
train: 600 muestras (para entrenar el clasificador)
válidos: 400 muestras (para calibrar las probabilidades predichas)
prueba: 1000 muestras
Observa que también creamos X_train_valid y y_train_valid, que consisten en los subconjuntos de entrenamiento y de validación. Esto se utiliza cuando sólo queremos entrenar el clasificador pero no calibrar las probabilidades predichas.
# Author: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
# License: BSD Style.
import numpy as np
from sklearn.datasets import make_blobs
np.random.seed(0)
X, y = make_blobs(n_samples=2000, n_features=2, centers=3, random_state=42,
cluster_std=5.0)
X_train, y_train = X[:600], y[:600]
X_valid, y_valid = X[600:1000], y[600:1000]
X_train_valid, y_train_valid = X[:1000], y[:1000]
X_test, y_test = X[1000:], y[1000:]
Ajuste y Calibración¶
En primer lugar, entrenaremos un RandomForestClassifier con 25 estimadores base (árboles) en los datos concatenados de entrenamiento y validación (1000 muestras). Este es el clasificador no calibrado.
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train_valid, y_train_valid)
Para entrenar el clasificador calibrado, empezamos con la misma RandomForestClassifier pero lo entrenamos usando sólo el subconjunto de datos de entrenamiento (600 muestras) y luego lo calibramos, con method='sigmoid', usando el subconjunto de datos válidos (400 muestras) en un proceso de 2 etapas.
from sklearn.calibration import CalibratedClassifierCV
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train, y_train)
cal_clf = CalibratedClassifierCV(clf, method="sigmoid", cv="prefit")
cal_clf.fit(X_valid, y_valid)
Comparar probabilidades¶
A continuación, trazamos un 2-simplex con flechas que muestran el cambio en las probabilidades predichas de las muestras de prueba.
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 10))
colors = ["r", "g", "b"]
clf_probs = clf.predict_proba(X_test)
cal_clf_probs = cal_clf.predict_proba(X_test)
# Plot arrows
for i in range(clf_probs.shape[0]):
plt.arrow(clf_probs[i, 0], clf_probs[i, 1],
cal_clf_probs[i, 0] - clf_probs[i, 0],
cal_clf_probs[i, 1] - clf_probs[i, 1],
color=colors[y_test[i]], head_width=1e-2)
# Plot perfect predictions, at each vertex
plt.plot([1.0], [0.0], 'ro', ms=20, label="Class 1")
plt.plot([0.0], [1.0], 'go', ms=20, label="Class 2")
plt.plot([0.0], [0.0], 'bo', ms=20, label="Class 3")
# Plot boundaries of unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], 'k', label="Simplex")
# Annotate points 6 points around the simplex, and mid point inside simplex
plt.annotate(r'($\frac{1}{3}$, $\frac{1}{3}$, $\frac{1}{3}$)',
xy=(1.0/3, 1.0/3), xytext=(1.0/3, .23), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.plot([1.0/3], [1.0/3], 'ko', ms=5)
plt.annotate(r'($\frac{1}{2}$, $0$, $\frac{1}{2}$)',
xy=(.5, .0), xytext=(.5, .1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($0$, $\frac{1}{2}$, $\frac{1}{2}$)',
xy=(.0, .5), xytext=(.1, .5), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($\frac{1}{2}$, $\frac{1}{2}$, $0$)',
xy=(.5, .5), xytext=(.6, .6), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($0$, $0$, $1$)',
xy=(0, 0), xytext=(.1, .1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($1$, $0$, $0$)',
xy=(1, 0), xytext=(1, .1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($0$, $1$, $0$)',
xy=(0, 1), xytext=(.1, 1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
# Add grid
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], 'k', alpha=0.2)
plt.plot([0, 0 + (1-x)/2], [x, x + (1-x)/2], 'k', alpha=0.2)
plt.plot([x, x + (1-x)/2], [0, 0 + (1-x)/2], 'k', alpha=0.2)
plt.title("Change of predicted probabilities on test samples "
"after sigmoid calibration")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
_ = plt.legend(loc="best")
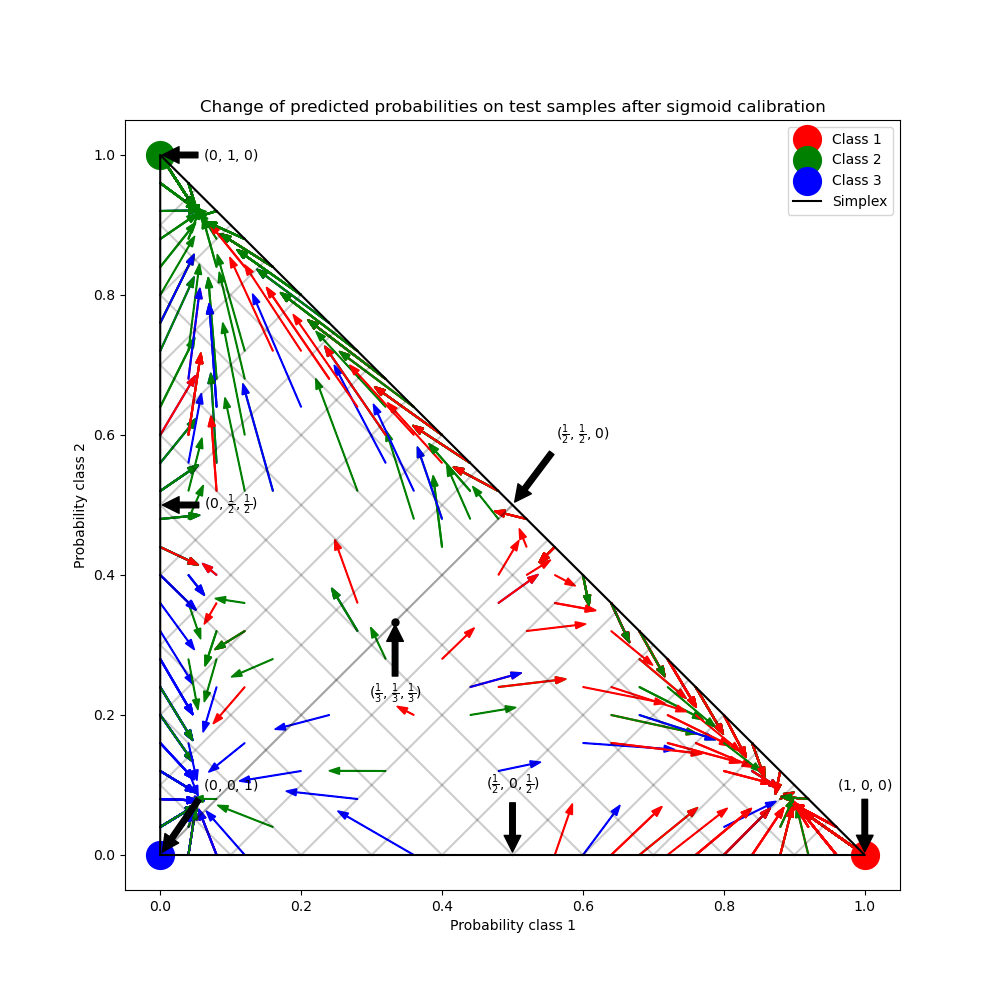
En la figura anterior, cada vértice del simplex representa una clase perfectamente predicha (por ejemplo, 1, 0, 0). El punto medio dentro del simplex representa la predicción de las tres clases con igual probabilidad (es decir, 1/3, 1/3, 1/3). Cada flecha comienza en las probabilidades no calibradas y termina con la punta de la flecha en la probabilidad calibrada. El color de la flecha representa la clase verdadera de esa muestra de prueba.
El clasificador no calibrado es demasiado confiado en sus predicciones e incurre en una gran pérdida log. El clasificador calibrado incurre en una pérdida log menor debido a dos factores. En primer lugar, observe en la figura anterior que las flechas generalmente apuntan lejos de los bordes del simplex, donde la probabilidad de una clase es 0. En segundo lugar, una gran proporción de las flechas apuntan hacia la clase verdadera, por ejemplo, las flechas verdes (muestras en las que la clase verdadera es «verde») generalmente apuntan hacia el vértice verde. Esto da lugar a un menor número de probabilidades predichas de 0 y, al mismo tiempo, a un aumento de las probabilidades predichas de la clase correcta. Así, el clasificador calibrado produce probabilidades predichas más precisas que incurren en una menor pérdida lógica.
Podemos demostrarlo objetivamente comparando la pérdida log de los clasificadores no calibrados y calibrados en las predicciones de las 1000 muestras de prueba. Obsérvese que una alternativa habría sido aumentar el número de estimadores base (árboles) del RandomForestClassifier lo que habría dado lugar a una disminución similar de log loss.
Out:
Log-loss of
* uncalibrated classifier: 1.290
* calibrated classifier: 0.549
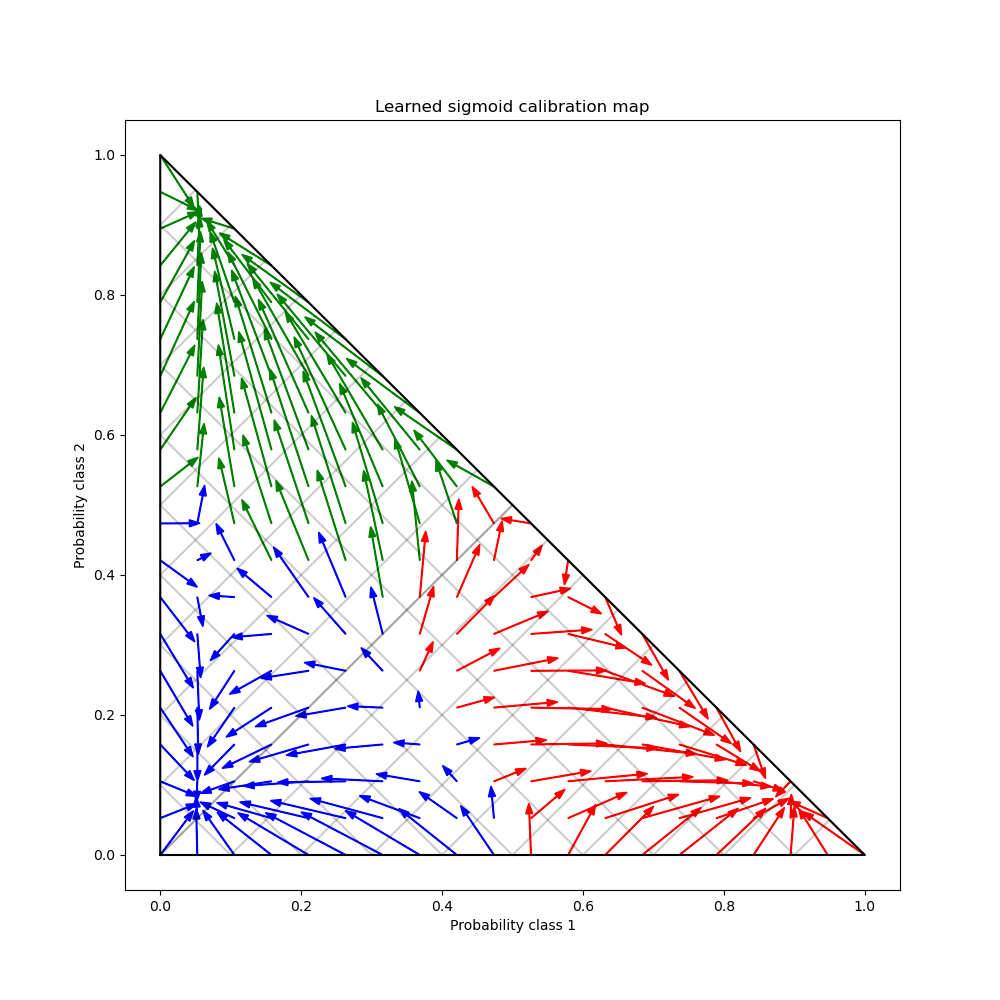
Por último, generamos una cuadrícula de posibles probabilidades no calibradas sobre el complejo de 2, calculamos las correspondientes probabilidades calibradas y trazamos flechas para cada una de ellas. Las flechas están coloreadas según la probabilidad no calibrada más alta. Esto ilustra el mapa de calibración aprendido:
plt.figure(figsize=(10, 10))
# Generate grid of probability values
p1d = np.linspace(0, 1, 20)
p0, p1 = np.meshgrid(p1d, p1d)
p2 = 1 - p0 - p1
p = np.c_[p0.ravel(), p1.ravel(), p2.ravel()]
p = p[p[:, 2] >= 0]
# Use the three class-wise calibrators to compute calibrated probabilities
calibrated_classifier = cal_clf.calibrated_classifiers_[0]
prediction = np.vstack([calibrator.predict(this_p)
for calibrator, this_p in
zip(calibrated_classifier.calibrators, p.T)]).T
# Re-normalize the calibrated predictions to make sure they stay inside the
# simplex. This same renormalization step is performed internally by the
# predict method of CalibratedClassifierCV on multiclass problems.
prediction /= prediction.sum(axis=1)[:, None]
# Plot changes in predicted probabilities induced by the calibrators
for i in range(prediction.shape[0]):
plt.arrow(p[i, 0], p[i, 1],
prediction[i, 0] - p[i, 0], prediction[i, 1] - p[i, 1],
head_width=1e-2, color=colors[np.argmax(p[i])])
# Plot the boundaries of the unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], 'k', label="Simplex")
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], 'k', alpha=0.2)
plt.plot([0, 0 + (1-x)/2], [x, x + (1-x)/2], 'k', alpha=0.2)
plt.plot([x, x + (1-x)/2], [0, 0 + (1-x)/2], 'k', alpha=0.2)
plt.title("Learned sigmoid calibration map")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.show()
Tiempo total de ejecución del script: (0 minutos 2.063 segundos)
