Curvas de probabilidad de calibración

Cuando se realiza una clasificación, a menudo se quiere predecir no sólo la etiqueta de la clase, sino también la probabilidad asociada. Esta probabilidad da algún tipo de confianza en la predicción. Este ejemplo demuestra cómo mostrar lo bien calibradas que están las probabilidades predichas y cómo calibrar un clasificador no calibrado.

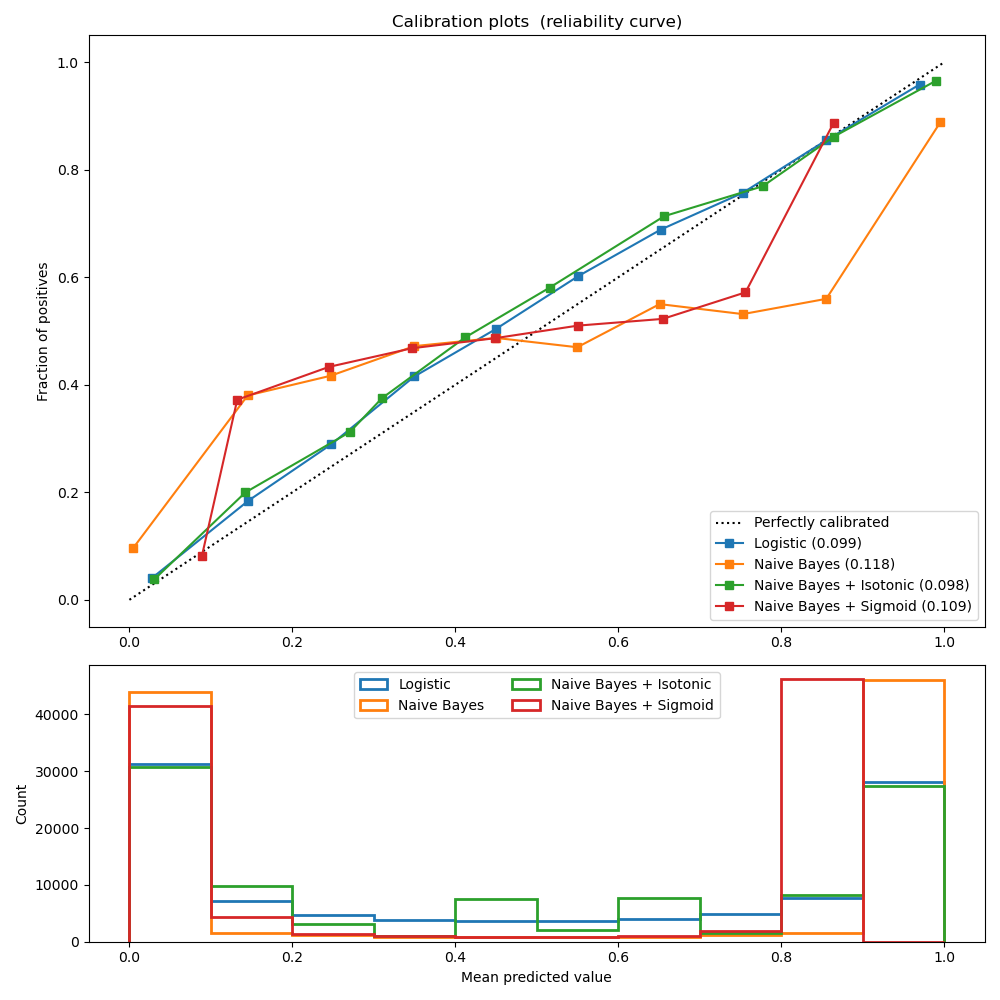
El experimento se realiza en un conjunto de datos artificial para la clasificación binaria con 100.000 muestras (1.000 de ellas se utilizan para el ajuste del modelo) con 20 características. De las 20 características, sólo 2 son informativas y 10 son redundantes. La primera figura muestra las probabilidades estimadas obtenidas con regresión logística, Bayes ingenuo gaussiano y Bayes ingenuo gaussiano con calibración isotónica y calibración sigmoidea. El rendimiento de la calibración se evalúa con la puntuación de Brier, indicada en la leyenda (cuanto más pequeña, mejor). Se puede observar aquí que la regresión logística está bien calibrada mientras que el Bayes ingenuo gaussiano crudo tiene un rendimiento muy malo. Esto se debe a las características redundantes que violan la suposición de la independencia de las características y dan lugar a un clasificador demasiado confiado, lo que se indica con la típica curva transpuesta-sigmoide.

La calibración de las probabilidades del Bayes ingenuo gaussiano con una regresión isotónica puede solucionar este problema, como puede verse en la curva de calibración casi diagonal. La calibración sigmoidea también mejora ligeramente la puntuación de Brier, aunque no con tanta fuerza como la regresión isotónica no paramétrica. Esto puede atribuirse al hecho de que tenemos muchos datos de calibración, de modo que se puede aprovechar la mayor flexibilidad del modelo no paramétrico.

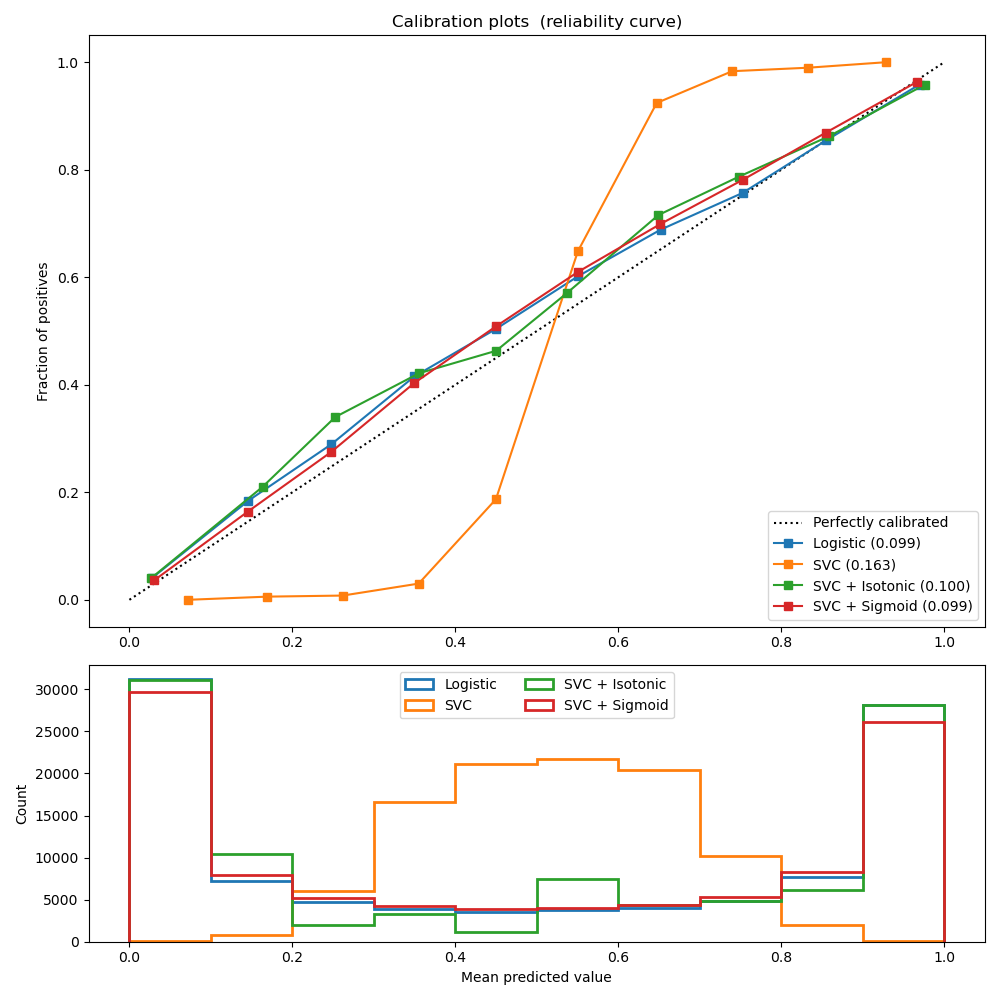
La segunda figura muestra la curva de calibración de un clasificador lineal de vectores de apoyo (LinearSVC). LinearSVC muestra el comportamiento opuesto al de los Bayes ingenuos gaussianos: la curva de calibración tiene una curva sigmoidea, lo que es típico de un clasificador poco fiable. En el caso de LinearSVC, esto se debe a la propiedad de margen de la pérdida de bisagra, que permite al modelo centrarse en las muestras duras que están cerca del límite de decisión (los vectores de soporte).

Ambos tipos de calibración pueden solucionar este problema y producir resultados casi idénticos. Esto demuestra que la calibración sigmoidea puede resolver situaciones en las que la curva de calibración del clasificador base es sigmoidea (por ejemplo, para LinearSVC) pero no cuando es transpuesta-sigmoidea (por ejemplo, gaussiano naive Bayes).

• 
• 

Out:

Logistic:
        Brier: 0.099
        Precision: 0.872
        Recall: 0.851
        F1: 0.862

Naive Bayes:
        Brier: 0.118
        Precision: 0.857
        Recall: 0.876
        F1: 0.867

Naive Bayes + Isotonic:
        Brier: 0.098
        Precision: 0.883
        Recall: 0.836
        F1: 0.859

Naive Bayes + Sigmoid:
        Brier: 0.109
        Precision: 0.861
        Recall: 0.871
        F1: 0.866

Logistic:
        Brier: 0.099
        Precision: 0.872
        Recall: 0.851
        F1: 0.862

SVC:
        Brier: 0.163
        Precision: 0.872
        Recall: 0.852
        F1: 0.862

SVC + Isotonic:
        Brier: 0.100
        Precision: 0.853
        Recall: 0.878
        F1: 0.865

SVC + Sigmoid:
        Brier: 0.099
        Precision: 0.874
        Recall: 0.849
        F1: 0.861

print(__doc__)

# Author: Alexandre Gramfort <alexandre.gramfort@telecom-paristech.fr>
#         Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
# License: BSD Style.

import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import (brier_score_loss, precision_score, recall_score,
                             f1_score)
from sklearn.calibration import CalibratedClassifierCV, calibration_curve
from sklearn.model_selection import train_test_split


# Create dataset of classification task with many redundant and few
# informative features
X, y = datasets.make_classification(n_samples=100000, n_features=20,
                                    n_informative=2, n_redundant=10,
                                    random_state=42)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.99,
                                                    random_state=42)


def plot_calibration_curve(est, name, fig_index):
    """Plot calibration curve for est w/o and with calibration. """
    # Calibrated with isotonic calibration
    isotonic = CalibratedClassifierCV(est, cv=2, method='isotonic')

    # Calibrated with sigmoid calibration
    sigmoid = CalibratedClassifierCV(est, cv=2, method='sigmoid')

    # Logistic regression with no calibration as baseline
    lr = LogisticRegression(C=1.)

    fig = plt.figure(fig_index, figsize=(10, 10))
    ax1 = plt.subplot2grid((3, 1), (0, 0), rowspan=2)
    ax2 = plt.subplot2grid((3, 1), (2, 0))

    ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
    for clf, name in [(lr, 'Logistic'),
                      (est, name),
                      (isotonic, name + ' + Isotonic'),
                      (sigmoid, name + ' + Sigmoid')]:
        clf.fit(X_train, y_train)
        y_pred = clf.predict(X_test)
        if hasattr(clf, "predict_proba"):
            prob_pos = clf.predict_proba(X_test)[:, 1]
        else:  # use decision function
            prob_pos = clf.decision_function(X_test)
            prob_pos = \
                (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())

        clf_score = brier_score_loss(y_test, prob_pos, pos_label=y.max())
        print("%s:" % name)
        print("\tBrier: %1.3f" % (clf_score))
        print("\tPrecision: %1.3f" % precision_score(y_test, y_pred))
        print("\tRecall: %1.3f" % recall_score(y_test, y_pred))
        print("\tF1: %1.3f\n" % f1_score(y_test, y_pred))

        fraction_of_positives, mean_predicted_value = \
            calibration_curve(y_test, prob_pos, n_bins=10)

        ax1.plot(mean_predicted_value, fraction_of_positives, "s-",
                 label="%s (%1.3f)" % (name, clf_score))

        ax2.hist(prob_pos, range=(0, 1), bins=10, label=name,
                 histtype="step", lw=2)

    ax1.set_ylabel("Fraction of positives")
    ax1.set_ylim([-0.05, 1.05])
    ax1.legend(loc="lower right")
    ax1.set_title('Calibration plots  (reliability curve)')

    ax2.set_xlabel("Mean predicted value")
    ax2.set_ylabel("Count")
    ax2.legend(loc="upper center", ncol=2)

    plt.tight_layout()

# Plot calibration curve for Gaussian Naive Bayes
plot_calibration_curve(GaussianNB(), "Naive Bayes", 1)

# Plot calibration curve for Linear SVC
plot_calibration_curve(LinearSVC(max_iter=10000), "SVC", 2)

plt.show()