1.15. Regresión isotónica¶
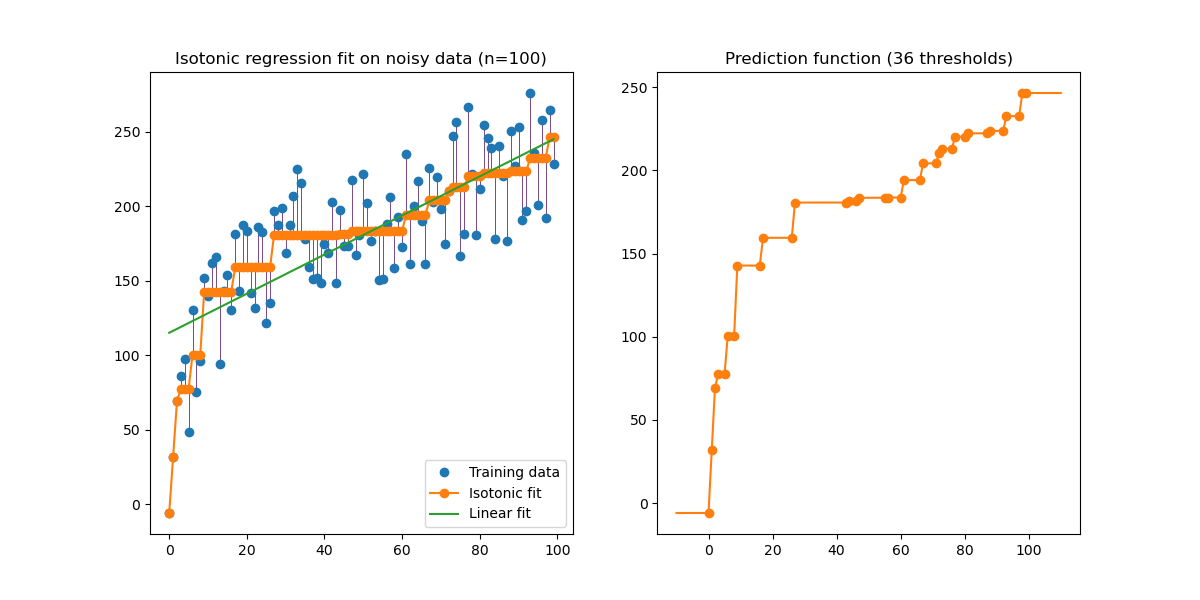
La clase IsotonicRegression ajusta una función real no decreciente a datos unidimensionales. Resuelve el siguiente problema:
minimize \(\sum_i w_i (y_i - \hat{y}_i)^2\)
subject to \(\hat{y}_i \le \hat{y}_j\) whenever \(X_i \le X_j\),
donde los pesos \(w_i\) son estrictamente positivos, y tanto X como y son cantidades reales arbitrarias.
El parámetro increasing cambia la restricción a \(\hat{y}_i \ge \hat{y}_j\) siempre que \(X_i \le X_j\). Si se configura como auto se elegirá automáticamente la restricción basada en el coeficiente de correlación por rangos de Spearman <https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient>`_.
La clase IsotonicRegression produce una serie de predicciones \(\hat{y}_i\) para los datos de entrenamiento que son los más cercanos a los objetivos \(y\) en términos de error cuadrático medio. Estas predicciones se interpolan para predecir a los datos no observados. Las predicciones de IsotonicRegression forman así una función que es lineal definida a trozos (piecewise):