Regresión Isotónica

Una ilustración de la regresión isotónica sobre los datos generados (tendencia monótona no lineal con ruido uniforme homoscedástico).

El algoritmo de regresión isotónica encuentra una aproximación no decreciente de una función minimizando el error cuadrático medio en los datos de entrenamiento. El beneficio de este modelo no paramétrico es que no asume ninguna forma para la función objetivo además de la monotonicidad. A modo de comparación, también se presenta una regresión lineal.

El gráfico de la derecha muestra la función de predicción del modelo que resulta de la interpolación lineal de los puntos de los umbrales. Los puntos de umbral son un subconjunto de las observaciones de entrada de entrenamiento y sus valores objetivo correspondientes se calculan mediante el ajuste isotónico no paramétrico.

print(__doc__)

# Author: Nelle Varoquaux <nelle.varoquaux@gmail.com>
#         Alexandre Gramfort <alexandre.gramfort@inria.fr>
# License: BSD

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection

from sklearn.linear_model import LinearRegression
from sklearn.isotonic import IsotonicRegression
from sklearn.utils import check_random_state

n = 100
x = np.arange(n)
rs = check_random_state(0)
y = rs.randint(-50, 50, size=(n,)) + 50. * np.log1p(np.arange(n))

Ajustar los modelos IsotonicRegression y LinearRegression:

ir = IsotonicRegression(out_of_bounds="clip")
y_ = ir.fit_transform(x, y)

lr = LinearRegression()
lr.fit(x[:, np.newaxis], y)  # x needs to be 2d for LinearRegression

LinearRegression

LinearRegression()

Gráfico de los resultados:

segments = [[[i, y[i]], [i, y_[i]]] for i in range(n)]
lc = LineCollection(segments, zorder=0)
lc.set_array(np.ones(len(y)))
lc.set_linewidths(np.full(n, 0.5))

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(12, 6))

ax0.plot(x, y, 'C0.', markersize=12)
ax0.plot(x, y_, 'C1.-', markersize=12)
ax0.plot(x, lr.predict(x[:, np.newaxis]), 'C2-')
ax0.add_collection(lc)
ax0.legend(('Training data', 'Isotonic fit', 'Linear fit'), loc='lower right')
ax0.set_title('Isotonic regression fit on noisy data (n=%d)' % n)

x_test = np.linspace(-10, 110, 1000)
ax1.plot(x_test, ir.predict(x_test), 'C1-')
ax1.plot(ir.X_thresholds_, ir.y_thresholds_, 'C1.', markersize=12)
ax1.set_title("Prediction function (%d thresholds)" % len(ir.X_thresholds_))

plt.show()

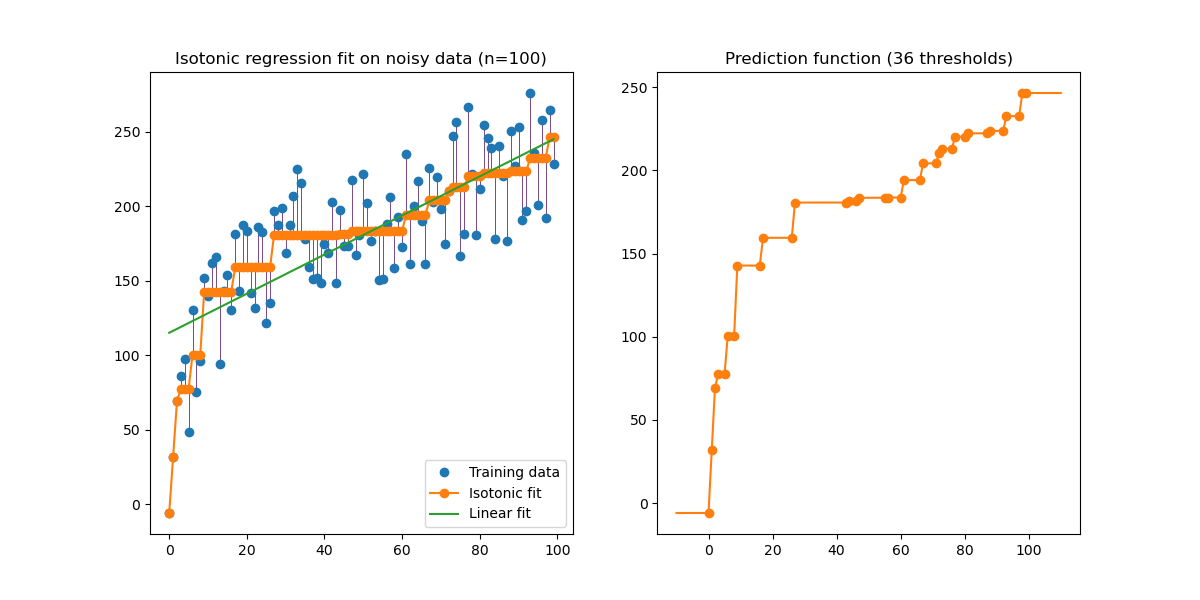
Ten en cuenta que pasamos explícitamente out_of_bounds="clip" al constructor de IsotonicRegression para controlar la forma en que el modelo extrapola fuera del rango de datos observados en el conjunto de entrenamiento. Esta extrapolación de «recorte» puede verse en el gráfico de la función de decisión de la derecha.