Detección compresiva: reconstrucción de la tomografía con a priori L1 (Lasso)

Este ejemplo muestra la reconstrucción de una imagen a partir de un conjunto de proyecciones paralelas, adquiridas a lo largo de diferentes ángulos. Este conjunto de datos se adquiere en tomografía computarizada (TC).

Sin ninguna información previa sobre la muestra, el número de proyecciones necesarias para reconstruir la imagen es del orden del tamaño lineal l de la imagen (en píxeles). Para simplificar, consideramos aquí una imagen dispersa, en la que sólo los píxeles de los límites de los objetos tienen un valor distinto de cero. Estos datos podrían corresponder, por ejemplo, a un material celular. Sin embargo, hay que tener en cuenta que la mayoría de las imágenes son dispersas en una base diferente, como las ondículas de Haar. Sólo se adquieren proyecciones l/7, por lo que es necesario utilizar la información previa disponible sobre la muestra (su escasez): es un ejemplo de detección compresiva.

La operación de proyección de la tomografía es una transformación lineal. Además del término de fidelidad de los datos correspondiente a una regresión lineal, penalizamos la norma L1 de la imagen para tener en cuenta su escasez. El problema de optimización resultante se denomina Lasso. Utilizamos la clase Lasso, que utiliza el algoritmo de descenso de coordenadas. Es importante destacar que esta implementación es más eficiente computacionalmente en una matriz dispersa, que el operador de proyección utilizado aquí.

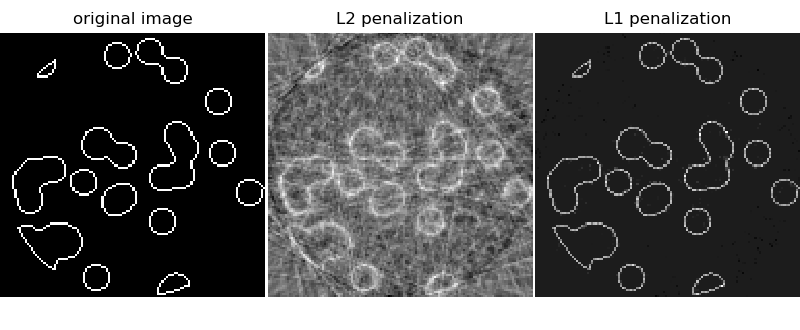
La reconstrucción con penalización L1 da un resultado con error cero (todos los píxeles se etiquetan con éxito con 0 o 1), aunque se haya añadido ruido a las proyecciones. En comparación, una penalización L2 (Ridge) produce un gran número de errores de etiquetado para los píxeles. Se observan importantes artefactos en la imagen reconstruida, al contrario que con la penalización L1. Nótese en particular el artefacto circular que separa los píxeles de las esquinas, que han contribuido a menos proyecciones que el disco central.

print(__doc__)

# Author: Emmanuelle Gouillart <emmanuelle.gouillart@nsup.org>
# License: BSD 3 clause

import numpy as np
from scipy import sparse
from scipy import ndimage
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt


def _weights(x, dx=1, orig=0):
    x = np.ravel(x)
    floor_x = np.floor((x - orig) / dx).astype(np.int64)
    alpha = (x - orig - floor_x * dx) / dx
    return np.hstack((floor_x, floor_x + 1)), np.hstack((1 - alpha, alpha))


def _generate_center_coordinates(l_x):
    X, Y = np.mgrid[:l_x, :l_x].astype(np.float64)
    center = l_x / 2.
    X += 0.5 - center
    Y += 0.5 - center
    return X, Y


def build_projection_operator(l_x, n_dir):
    """ Compute the tomography design matrix.

    Parameters
    ----------

    l_x : int
        linear size of image array

    n_dir : int
        number of angles at which projections are acquired.

    Returns
    -------
    p : sparse matrix of shape (n_dir l_x, l_x**2)
    """
    X, Y = _generate_center_coordinates(l_x)
    angles = np.linspace(0, np.pi, n_dir, endpoint=False)
    data_inds, weights, camera_inds = [], [], []
    data_unravel_indices = np.arange(l_x ** 2)
    data_unravel_indices = np.hstack((data_unravel_indices,
                                      data_unravel_indices))
    for i, angle in enumerate(angles):
        Xrot = np.cos(angle) * X - np.sin(angle) * Y
        inds, w = _weights(Xrot, dx=1, orig=X.min())
        mask = np.logical_and(inds >= 0, inds < l_x)
        weights += list(w[mask])
        camera_inds += list(inds[mask] + i * l_x)
        data_inds += list(data_unravel_indices[mask])
    proj_operator = sparse.coo_matrix((weights, (camera_inds, data_inds)))
    return proj_operator


def generate_synthetic_data():
    """ Synthetic binary data """
    rs = np.random.RandomState(0)
    n_pts = 36
    x, y = np.ogrid[0:l, 0:l]
    mask_outer = (x - l / 2.) ** 2 + (y - l / 2.) ** 2 < (l / 2.) ** 2
    mask = np.zeros((l, l))
    points = l * rs.rand(2, n_pts)
    mask[(points[0]).astype(int), (points[1]).astype(int)] = 1
    mask = ndimage.gaussian_filter(mask, sigma=l / n_pts)
    res = np.logical_and(mask > mask.mean(), mask_outer)
    return np.logical_xor(res, ndimage.binary_erosion(res))


# Generate synthetic images, and projections
l = 128
proj_operator = build_projection_operator(l, l // 7)
data = generate_synthetic_data()
proj = proj_operator @ data.ravel()[:, np.newaxis]
proj += 0.15 * np.random.randn(*proj.shape)

# Reconstruction with L2 (Ridge) penalization
rgr_ridge = Ridge(alpha=0.2)
rgr_ridge.fit(proj_operator, proj.ravel())
rec_l2 = rgr_ridge.coef_.reshape(l, l)

# Reconstruction with L1 (Lasso) penalization
# the best value of alpha was determined using cross validation
# with LassoCV
rgr_lasso = Lasso(alpha=0.001)
rgr_lasso.fit(proj_operator, proj.ravel())
rec_l1 = rgr_lasso.coef_.reshape(l, l)

plt.figure(figsize=(8, 3.3))
plt.subplot(131)
plt.imshow(data, cmap=plt.cm.gray, interpolation='nearest')
plt.axis('off')
plt.title('original image')
plt.subplot(132)
plt.imshow(rec_l2, cmap=plt.cm.gray, interpolation='nearest')
plt.title('L2 penalization')
plt.axis('off')
plt.subplot(133)
plt.imshow(rec_l1, cmap=plt.cm.gray, interpolation='nearest')
plt.title('L1 penalization')
plt.axis('off')

plt.subplots_adjust(hspace=0.01, wspace=0.01, top=1, bottom=0, left=0,
                    right=1)

plt.show()