Detección de valores atípicos en un conjunto de datos reales

Este ejemplo ilustra la necesidad de una estimación robusta de la covarianza en un conjunto de datos reales. Es útil tanto para la detección de valores atípicos como para una mejor comprensión de la estructura de los datos.

Seleccionamos dos conjuntos de dos variables del conjunto de datos de viviendas de Boston como ilustración del tipo de análisis que puede realizarse con varias herramientas de detección de valores atípicos. A efectos de visualización, trabajamos con ejemplos bidimensionales, pero hay que tener en cuenta que las cosas no son tan triviales en alta dimensión, como se señalará.

En ambos ejemplos, el resultado principal es que la estimación empírica de la covarianza, como no robusta, está muy influenciada por la estructura heterogénea de las observaciones. Aunque la estimación robusta de la covarianza es capaz de centrarse en la modalidad principal de la distribución de los datos, se ciñe a la suposición de que los datos deben tener una distribución gaussiana, lo que da lugar a una estimación algo sesgada de la estructura de los datos, aunque precisa hasta cierto punto. La SVM de una clase no asume ninguna forma paramétrica de la distribución de los datos y, por lo tanto, puede modelar la forma compleja de los datos mucho mejor.

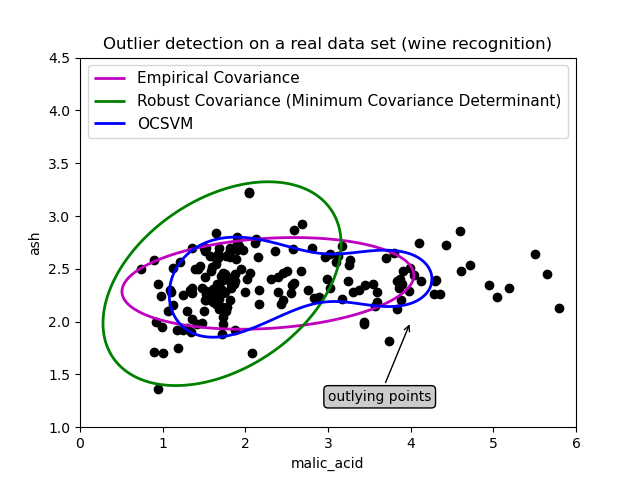
Primer ejemplo

El primer ejemplo ilustra cómo el estimador robusto del Determinante de Covarianza Mínimo puede ayudar a concentrarse en un conglomerado relevante cuando existen puntos periféricos. En este caso, la estimación de la covarianza empírica está sesgada por puntos fuera del clúster principal. Por supuesto, algunas herramientas de cribado habrían señalado la presencia de dos conglomerados (Máquinas de vectores de Soporte, modelos de mezclas gaussianas, detección de valores atípicos univariantes, …). Pero si se tratara de un ejemplo de alta dimensión, ninguna de ellas podría aplicarse tan fácilmente.

print(__doc__)

# Author: Virgile Fritsch <virgile.fritsch@inria.fr>
# License: BSD 3 clause

import numpy as np
from sklearn.covariance import EllipticEnvelope
from sklearn.svm import OneClassSVM
import matplotlib.pyplot as plt
import matplotlib.font_manager
from sklearn.datasets import load_wine

# Define "classifiers" to be used
classifiers = {
    "Empirical Covariance": EllipticEnvelope(support_fraction=1.,
                                             contamination=0.25),
    "Robust Covariance (Minimum Covariance Determinant)":
    EllipticEnvelope(contamination=0.25),
    "OCSVM": OneClassSVM(nu=0.25, gamma=0.35)}
colors = ['m', 'g', 'b']
legend1 = {}
legend2 = {}

# Get data
X1 = load_wine()['data'][:, [1, 2]]  # two clusters

# Learn a frontier for outlier detection with several classifiers
xx1, yy1 = np.meshgrid(np.linspace(0, 6, 500), np.linspace(1, 4.5, 500))
for i, (clf_name, clf) in enumerate(classifiers.items()):
    plt.figure(1)
    clf.fit(X1)
    Z1 = clf.decision_function(np.c_[xx1.ravel(), yy1.ravel()])
    Z1 = Z1.reshape(xx1.shape)
    legend1[clf_name] = plt.contour(
        xx1, yy1, Z1, levels=[0], linewidths=2, colors=colors[i])

legend1_values_list = list(legend1.values())
legend1_keys_list = list(legend1.keys())

# Plot the results (= shape of the data points cloud)
plt.figure(1)  # two clusters
plt.title("Outlier detection on a real data set (wine recognition)")
plt.scatter(X1[:, 0], X1[:, 1], color='black')
bbox_args = dict(boxstyle="round", fc="0.8")
arrow_args = dict(arrowstyle="->")
plt.annotate("outlying points", xy=(4, 2),
             xycoords="data", textcoords="data",
             xytext=(3, 1.25), bbox=bbox_args, arrowprops=arrow_args)
plt.xlim((xx1.min(), xx1.max()))
plt.ylim((yy1.min(), yy1.max()))
plt.legend((legend1_values_list[0].collections[0],
            legend1_values_list[1].collections[0],
            legend1_values_list[2].collections[0]),
           (legend1_keys_list[0], legend1_keys_list[1], legend1_keys_list[2]),
           loc="upper center",
           prop=matplotlib.font_manager.FontProperties(size=11))
plt.ylabel("ash")
plt.xlabel("malic_acid")

plt.show()

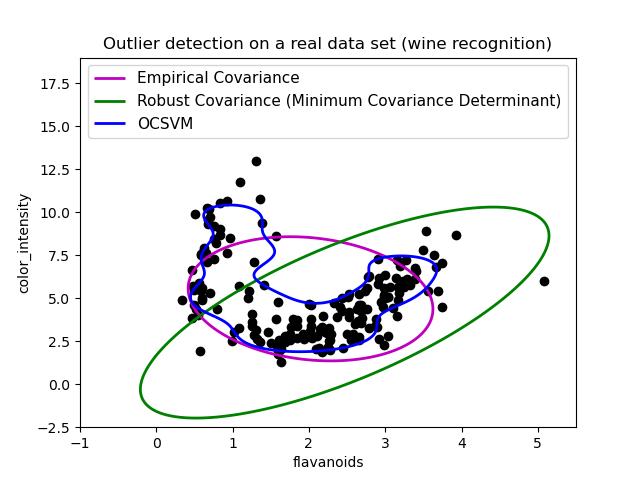
Segundo ejemplo

El segundo ejemplo muestra la capacidad del estimador robusto del Determinante Mínimo de la Covarianza para concentrarse en el modo principal de la distribución de los datos: la localización parece estar bien estimada, aunque la covarianza es difícil de estimar debido a la distribución en forma de plátano. De todos modos, podemos deshacernos de algunas observaciones periféricas. La SVM de una clase es capaz de capturar la estructura real de los datos, pero la dificultad estriba en ajustar su parámetro de ancho de banda del núcleo para obtener un buen compromiso entre la forma de la matriz de dispersión de los datos y el riesgo de sobreajuste de los datos.

# Get data
X2 = load_wine()['data'][:, [6, 9]]  # "banana"-shaped

# Learn a frontier for outlier detection with several classifiers
xx2, yy2 = np.meshgrid(np.linspace(-1, 5.5, 500), np.linspace(-2.5, 19, 500))
for i, (clf_name, clf) in enumerate(classifiers.items()):
    plt.figure(2)
    clf.fit(X2)
    Z2 = clf.decision_function(np.c_[xx2.ravel(), yy2.ravel()])
    Z2 = Z2.reshape(xx2.shape)
    legend2[clf_name] = plt.contour(
        xx2, yy2, Z2, levels=[0], linewidths=2, colors=colors[i])

legend2_values_list = list(legend2.values())
legend2_keys_list = list(legend2.keys())

# Plot the results (= shape of the data points cloud)
plt.figure(2)  # "banana" shape
plt.title("Outlier detection on a real data set (wine recognition)")
plt.scatter(X2[:, 0], X2[:, 1], color='black')
plt.xlim((xx2.min(), xx2.max()))
plt.ylim((yy2.min(), yy2.max()))
plt.legend((legend2_values_list[0].collections[0],
            legend2_values_list[1].collections[0],
            legend2_values_list[2].collections[0]),
           (legend2_keys_list[0], legend2_keys_list[1], legend2_keys_list[2]),
           loc="upper center",
           prop=matplotlib.font_manager.FontProperties(size=11))
plt.ylabel("color_intensity")
plt.xlabel("flavanoids")

plt.show()