Aspectos Destacados de scikit-learn 0.24

¡Nos complace anunciar el lanzamiento de scikit-learn 0.24! Se han añadido muchas correcciones de errores y mejoras, así como algunas nuevas características clave. A continuación detallamos algunas de las principales características de esta versión. Para una lista exhaustiva de todos los cambios, por favor consulta las notas de publicación.

Para instalar la última versión (con pip):

pip install --upgrade scikit-learn

o con conda:

conda install -c conda-forge scikit-learn

Estimadores Sucesivos de Reducción a la Mitad para ajustar los hiperparámetros

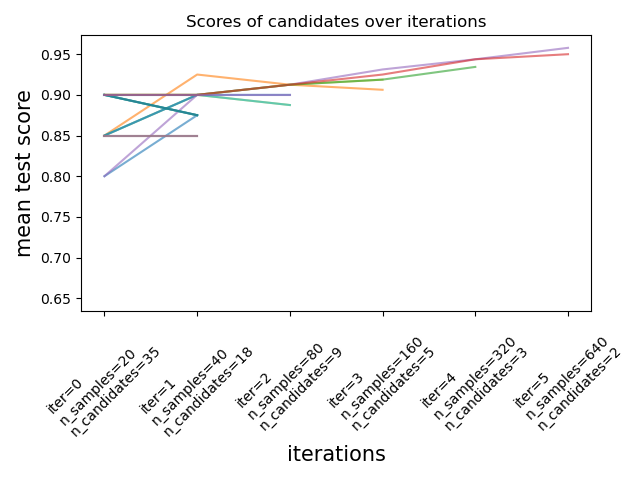
El método Successive Halving (división sucesiva a la mitad), un método de vanguardia, está ahora disponible para explorar el espacio de los parámetros e identificar su mejor combinación. HalvingGridSearchCV y HalvingRandomSearchCV pueden utilizarse como sustitutos de GridSearchCV y RandomizedSearchCV. La reducción sucesiva a la mitad es un proceso de selección iterativo que se ilustra en la siguiente figura. La primera iteración se ejecuta con una pequeña cantidad de recursos, donde el recurso suele corresponder al número de muestras de entrenamiento, pero también puede ser un parámetro entero arbitrario como n_estimators en un bosque aleatorio. Sólo un subconjunto de los parámetros candidatos se selecciona para la siguiente iteración, que se ejecutará con una cantidad creciente de recursos asignados. Sólo un subconjunto de candidatos durará hasta el final del proceso de iteración, y el mejor candidato a parámetro es el que tiene la mayor puntuación en la última iteración.

Lea más en el Manual de Usuario (Nota: los estimadores de Successive Halving todavía son experimentales).

import numpy as np
from scipy.stats import randint
from sklearn.experimental import enable_halving_search_cv  # noqa
from sklearn.model_selection import HalvingRandomSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification

rng = np.random.RandomState(0)

X, y = make_classification(n_samples=700, random_state=rng)

clf = RandomForestClassifier(n_estimators=10, random_state=rng)

param_dist = {"max_depth": [3, None],
              "max_features": randint(1, 11),
              "min_samples_split": randint(2, 11),
              "bootstrap": [True, False],
              "criterion": ["gini", "entropy"]}

rsh = HalvingRandomSearchCV(estimator=clf, param_distributions=param_dist,
                            factor=2, random_state=rng)
rsh.fit(X, y)
rsh.best_params_

Out:

{'bootstrap': True, 'criterion': 'gini', 'max_depth': None, 'max_features': 10, 'min_samples_split': 10}

Soporte nativo para características categóricas en estimadores HistGradientBoosting

HistGradientBoostingClassifier y HistGradientBoostingRegressor tienen ahora soporte nativo para características categóricas: pueden considerar divisiones en datos categóricos no ordenados. Lee más en el Manual de Usuario.

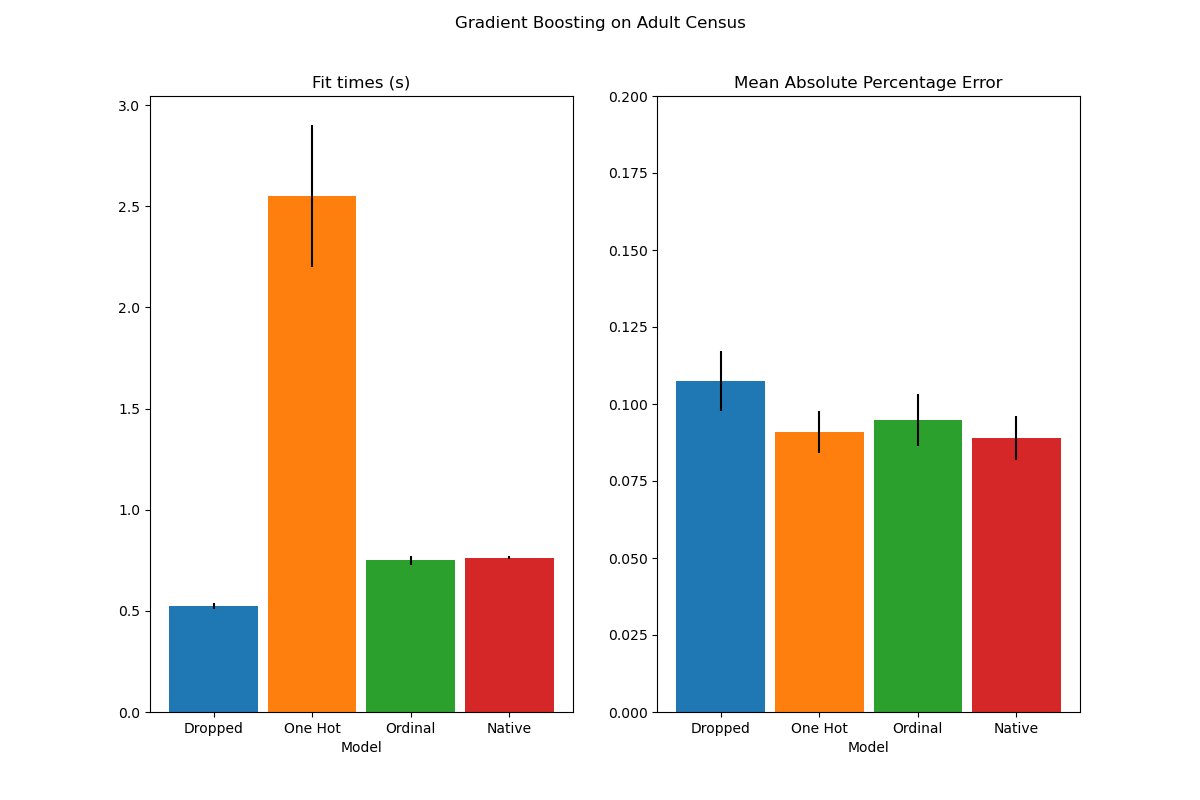
El gráfico muestra que el nuevo soporte nativo para las características categóricas conduce a tiempos de ajuste comparables a los de los modelos en los que las categorías se tratan como cantidades ordenadas, es decir, simplemente con codificación ordinal. El soporte nativo también es más expresivo que la codificación one-hot y la codificación ordinal. Sin embargo, para utilizar el nuevo parámetro categorical_features, sigue siendo necesario preprocesar los datos dentro de un pipeline como se demuestra en este ejemplo.

Mejora del rendimiento de los estimadores HistGradientBoosting

La huella de memoria de ensemble.HistGradientBoostingRegressor y ensemble.HistGradientBoostingClassifier se ha mejorado significativamente durante las invocaciones a fit. Además, la inicialización del histograma se realiza ahora en paralelo, lo que supone una ligera mejora de la velocidad. Puedes ver más en la página de Rendimiento (Benchmark).

Nuevo metaestimador de autoentrenamiento

Una nueva implementación de autoentrenamiento, basada en el algoritmo de Yarowski puede ahora utilizarse con cualquier clasificador que implemente predict_proba. El subclasificador se comportará como un clasificador semisupervisado, permitiéndole aprender de datos no etiquetados. Lee más en el Manual de Usuario.

import numpy as np
from sklearn import datasets
from sklearn.semi_supervised import SelfTrainingClassifier
from sklearn.svm import SVC

rng = np.random.RandomState(42)
iris = datasets.load_iris()
random_unlabeled_points = rng.rand(iris.target.shape[0]) < 0.3
iris.target[random_unlabeled_points] = -1
svc = SVC(probability=True, gamma="auto")
self_training_model = SelfTrainingClassifier(svc)
self_training_model.fit(iris.data, iris.target)

Out:

SelfTrainingClassifier(base_estimator=SVC(gamma='auto', probability=True))

Nuevo transformador SequentialFeatureSelector

Un nuevo transformador iterativo para seleccionar características está disponible: SequentialFeatureSelector. La Selección Secuencial de Características puede añadir características de una en una (selección hacia delante) o eliminar características de la lista de características disponibles (selección hacia atrás), basándose en una maximización de la puntuación de validación cruzada. Consulta el Manual de Usuario.

from sklearn.feature_selection import SequentialFeatureSelector
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris

X, y = load_iris(return_X_y=True, as_frame=True)
feature_names = X.columns
knn = KNeighborsClassifier(n_neighbors=3)
sfs = SequentialFeatureSelector(knn, n_features_to_select=2)
sfs.fit(X, y)
print("Features selected by forward sequential selection: "
      f"{feature_names[sfs.get_support()].tolist()}")

Out:

Features selected by forward sequential selection: ['petal length (cm)', 'petal width (cm)']

Nueva función de aproximación kernel PolynomialCountSketch

La nueva PolynomialCountSketch aproxima una expansión polinomial de un espacio de características cuando se utiliza con modelos lineales, pero utiliza mucha menos memoria que PolynomialFeatures.

from sklearn.datasets import fetch_covtype
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.kernel_approximation import PolynomialCountSketch
from sklearn.linear_model import LogisticRegression

X, y = fetch_covtype(return_X_y=True)
pipe = make_pipeline(MinMaxScaler(),
                     PolynomialCountSketch(degree=2, n_components=300),
                     LogisticRegression(max_iter=1000))
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=5000,
                                                    test_size=10000,
                                                    random_state=42)
pipe.fit(X_train, y_train).score(X_test, y_test)

Out:

0.7349

A modo de comparación, aquí está la puntuación de una línea de base lineal para los mismos datos:

linear_baseline = make_pipeline(MinMaxScaler(),
                                LogisticRegression(max_iter=1000))
linear_baseline.fit(X_train, y_train).score(X_test, y_test)

Out:

0.7137

Gráficos de Expectativas Condicionales Individuales

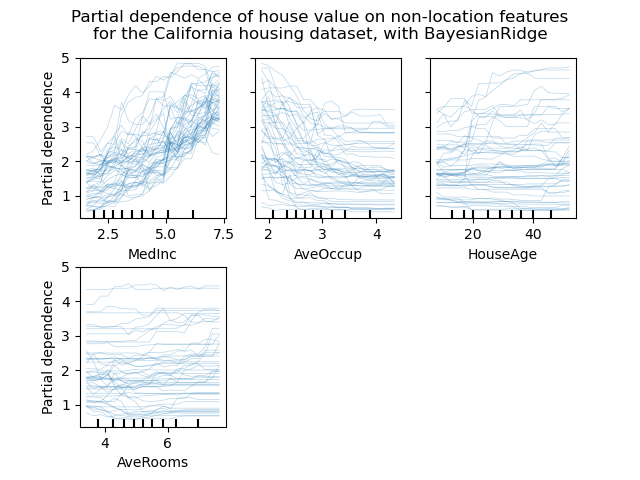
Existe un nuevo tipo de gráfico de dependencia parcial: el gráfico de Expectativa Condicional Individual (ICE). Los gráficos ICE visualizan la dependencia de la predicción de una característica para cada muestra por separado, con una línea por muestra. Consulta el Manual de Usuario

from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.inspection import plot_partial_dependence

X, y = fetch_california_housing(return_X_y=True, as_frame=True)
features = ['MedInc', 'AveOccup', 'HouseAge', 'AveRooms']
est = RandomForestRegressor(n_estimators=10)
est.fit(X, y)
display = plot_partial_dependence(
       est, X, features, kind="individual", subsample=50,
       n_jobs=3, grid_resolution=20, random_state=0
)
display.figure_.suptitle(
    'Partial dependence of house value on non-location features\n'
    'for the California housing dataset, with BayesianRidge'
)
display.figure_.subplots_adjust(hspace=0.3)

Nuevo criterio de división de Poisson para DecisionTreeRegressor

La integración de la estimación de la regresión de Poisson continúa desde la versión 0.23. DecisionTreeRegressor ahora soporta un nuevo criterio de división 'poisson'. Establecer criterio="poisson" puede ser una buena opción si tu objetivo es un recuento o una frecuencia.

from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
import numpy as np

n_samples, n_features = 1000, 20
rng = np.random.RandomState(0)
X = rng.randn(n_samples, n_features)
# positive integer target correlated with X[:, 5] with many zeros:
y = rng.poisson(lam=np.exp(X[:, 5]) / 2)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=rng)
regressor = DecisionTreeRegressor(criterion='poisson', random_state=0)
regressor.fit(X_train, y_train)

Out:

DecisionTreeRegressor(criterion='poisson', random_state=0)

Nuevas mejoras en la documentación

Se han añadido nuevos ejemplos y páginas de documentación, en un esfuerzo continuo por mejorar la comprensión de las prácticas de aprendizaje automático:

• una nueva sección sobre errores comunes y prácticas recomendadas,

• un ejemplo que ilustra cómo comparar estadísticamente el rendimiento de los modelos evaluados utilizando GridSearchCV,

• un ejemplo de cómo interpretar los coeficientes de los modelos lineales,

• un ejemplo comparando la Regresión de Componentes Principales y Mínimos Cuadrados Parciales.