4.1. Gráficos de Dependencia Parcial y de Expectativa Condicional Individual

Los gráficos de dependencia parcial (Partial dependence plots, PDP) y los gráficos de expectativas condicionales individuales (individual conditional expectation, ICE) pueden utilizarse para visualizar y analizar la interacción entre la respuesta objetivo 1 y un conjunto de características de entrada de interés.

Tanto los PDP como las ICE suponen que las características de entrada de interés son independientes de las características del complemento, y esta suposición a menudo se viola en la práctica. Así, en los casos de características correlacionadas, crearemos puntos de datos absurdos para calcular PDP/ICE.

4.1.1. Gráficos de dependencia parcial

Los gráficos de dependencia parcial (PDP) muestran la dependencia entre la respuesta objetivo y un conjunto de características de entrada de interés, marginando los valores de todas las demás características de entrada (las características “complementarias”). Intuitivamente, podemos interpretar la dependencia parcial como la respuesta objetivo esperada en función de las características de entrada de interés.

Debido a los límites de la percepción humana, el tamaño del conjunto de características de entrada de interés debe ser pequeño (normalmente, uno o dos), por lo que las características de entrada de interés suelen elegirse entre las más importantes.

La siguiente figura muestra dos gráficos de dependencia parcial unidireccionales y uno bidireccional para el conjunto de datos de viviendas de California, con un HistGradientBoostingRegressor:

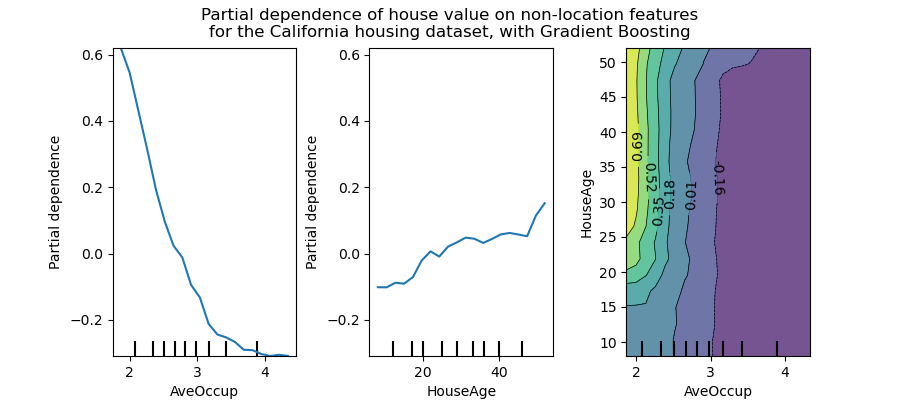
Los PDP unidireccionales nos informan de la interacción entre la respuesta objetivo y una característica de entrada de interés (por ejemplo, lineal, no lineal). El gráfico de la izquierda de la figura anterior muestra el efecto de la ocupación promedio sobre la mediana del precio de la vivienda; podemos ver claramente una relación lineal entre ellos cuando la ocupación promedio es inferior a 3 personas. Del mismo modo, podríamos analizar el efecto de la edad de la vivienda sobre la mediana del precio de la misma (gráfico central). Así pues, estas interpretaciones son marginales, considerando una característica a la vez.

Los PDP con dos características de entrada de interés muestran las interacciones entre las dos características. Por ejemplo, los PDP con dos variables en la figura anterior muestra la dependencia de la mediana del precio de la vivienda de los valores conjuntos de la edad de la vivienda y de los ocupantes promedio por hogar. Podemos ver claramente una interacción entre las dos características: para una ocupación promedio mayor que dos, el precio de la vivienda es casi independiente de la edad de la casa, mientras que para los valores menores que 2 hay una fuerte dependencia de la edad.

El módulo sklearn.inspection proporciona una función de conveniencia plot_partial_dependence para crear gráficos de dependencia parcial unidireccional y bidireccional. En el siguiente ejemplo se muestra cómo crear una cuadrícula de gráficos de dependencia parcial: dos PDP unidereccional para las características 0 y 1 y un PDP bidireccionales entre las dos características:

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import plot_partial_dependence

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> plot_partial_dependence(clf, X, features) 

Puedes acceder a los objetos figura y Ejes recién creados utilizando plt.gcf() y plt.gca().

Para la clasificación multiclase, es necesario establecer la etiqueta de clase para la que deben crearse los PDF mediante el argumento target:

>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10,
...     max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> plot_partial_dependence(mc_clf, X, features, target=0) 

El mismo parámetro target se utiliza para especificar el objetivo en las configuraciones de la regresión de salida múltiple.

Si necesitas los valores en bruto de la función de dependencia parcial en lugar de los gráficos, puedes utilizar la función sklearn.inspection.partial_dependence:

>>> from sklearn.inspection import partial_dependence

>>> pdp, axes = partial_dependence(clf, X, [0])
>>> pdp
array([[ 2.466...,  2.466..., ...
>>> axes
[array([-1.624..., -1.592..., ...

Los valores en los que debe evaluarse la dependencia parcial se generan directamente a partir de X. Para la dependencia parcial bidireccional, se genera una cuadrícula 2D de valores. El campo values devuelto por sklearn.inspection. artial_dependence da los valores reales utilizados en la cuadrícula para cada característica de entrada de interés. También corresponden al eje de los gráficos.

4.1.2. Gráfico de expectativas condicionales individuales (Individual conditional expectation, ICE)

De forma similar a los PDP, un gráfico de expectativas condicionales individuales (ICE) muestra la dependencia entre la función objetivo y una característica de entrada de interés. Sin embargo, a diferencia de un PDP, que muestra el efecto promedio de la característica de entrada, un gráfico ICE visualiza la dependencia de la predicción de una característica para cada muestra por separado con una línea por muestra. Debido a los límites de la percepción humana, sólo se admite una característica de entrada de interés para los gráficos de ICE.

Las siguientes figuras muestran cuatro gráficos de ICE para el conjunto de datos de viviendas de California, con un HistGradientBoostingRegressor. La segunda figura muestra la línea PD correspondiente a las líneas de ICE.

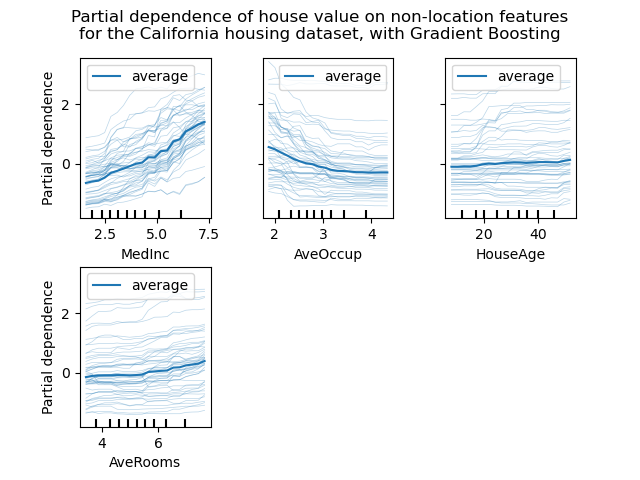
Mientras que los PDP son buenos para mostrar el efecto promedio de las características objetivo, pueden ocultar una relación heterogénea creada por las interacciones. Cuando las interacciones están presentes, el gráfico de ICE proporcionará muchas más perspectivas. Por ejemplo, podríamos observar una relación lineal entre la renta media y el precio de la vivienda en la línea PD. Sin embargo, las líneas ICE muestran que hay algunas excepciones, en las que el precio de la vivienda permanece constante en algunos rangos de la mediana del ingreso.

La función de conveniencia plot_partial_dependence del módulo sklearn.inspection puede utilizarse para crear gráficos de ICE estableciendo kind='individual'. En el siguiente ejemplo, te mostramos cómo crear una cuadrícula de gráficos de ICE:

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import plot_partial_dependence

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1]
>>> plot_partial_dependence(clf, X, features,
...     kind='individual')  

En los gráficos de ICE tal vez no sea fácil ver el efecto promedio de la característica de entrada de interés. Por lo tanto, se recomienda utilizar los gráficos ICE junto con los PDP. Pueden trazarse juntos con kind='both'.

>>> plot_partial_dependence(clf, X, features,
...     kind='both')  

4.1.3. Definición Matemática

Sea \(X_S\) el conjunto de características de entradas de interés (es decir, el parámetro features) y sea \(X_C\) su complemento.

La dependencia parcial de la respuesta \(f\) en un punto \(x_S\) se define como:

\[\begin{split}pd_{X_S}(x_S) &\overset{def}{=} \mathbb{E}_{X_C}\left[ f(x_S, X_C) \right]\\ &= \int f(x_S, x_C) p(x_C) dx_C,\end{split}\]

donde \(f(x_S, x_C)\) es la función de respuesta (predict, predict_proba o decision_function) para una muestra dada cuyos valores están definidos por \(x_S\) para las características en \(X_S\), y por \(x_C\) para las características en \(X_C\). Ten en cuenta que \(x_S\) y \(x_C\) pueden ser tuplas.

El cálculo de esta integral para varios valores de \(x_S\) produce un gráfico PDP como el de arriba. Una línea ICE se define como un solo \(f(x_{S}, x_{C}^{(i)})\) evaluado en \(x_{S}\).

4.1.4. Métodos de cálculo

Hay dos métodos principales para aproximar la integral anterior, a saber, los métodos “brute” y “recursión”. El parámetro method controla el método a utilizar.

El método “brute” es un método genérico que funciona con cualquier estimador. Ten en cuenta que el cálculo de los gráficos ICE sólo es posible con el método “brute”. Aproxima la integral anterior calculando un promedio sobre los datos X:

\[pd_{X_S}(x_S) \approx \frac{1}{n_\text{samples}} \sum_{i=1}^n f(x_S, x_C^{(i)}),\]

donde \(x_C^{(i)}\) es valor de la i-ésima muestra para las características en \(X_C\). Para cada valor de \(x_S\), este método requiere una pasada completa por el conjunto de datos X lo cual es intensivo computacionalmente.

Cada uno de las \(f(x_{S}, x_{C}^{(i)})\) corresponde a una línea ICE evaluada en \(x_{S}\). Calculando esto para múltiples valores de \(x_{S}\), se obtiene una línea ICE completa. Como se puede ver, el promedio de las líneas ICE corresponde a la línea de dependencia parcial.

El método “recursion” es más rápido que el método “brute”, pero sólo admite para los gráficos PDP mediante algunos estimadores basados en árboles. Se calcula como sigue. Para un punto dado \(x_S\), se realiza un recorrido a un árbol ponderado: si un nodo dividido involucra una característica de entrada de interés, se sigue la rama izquierda o derecha correspondiente; de lo contrario, se siguen ambas ramas, cada rama siendo ponderada por la fracción de muestras de entrenamiento que entraron en esa rama. Por último, la dependencia parcial viene dada por un promedio ponderado de todos los valores de las hojas visitadas.

Con el método “brute”, el parámetro X se utiliza tanto para generar la cuadrícula de valores \(x_S\) como los valores de características del complemento \(x_C\). Sin embargo, con el método “recursion”, X sólo se utiliza para los valores de la cuadrícula: implícitamente, los valores \(x_C\) son los de los datos de entrenamiento.

Por defecto, el método “recursion” es utilizado para graficar los PDP en los estimadores basados en un árbol que lo admiten, y “brute” se utiliza para el resto.

Nota

Aunque ambos métodos deberían ser parecidos en general, podrían diferir en algunos ajustes específicos. El método “brute” asume la existencia de los puntos de datos \((x_S, x_C^{(i)})\). Cuando las características están correlacionadas, estas muestras artificiales pueden tener una masa de probabilidad muy baja. Los métodos “brute” y “recursion” probablemente no estén de acuerdo con el valor de la dependencia parcial, porque tratarán estas poco probables muestras de forma diferente. Recuerda, sin embargo, que la suposición principal para interpretar los PDP es que las características deben ser independientes.

Ejemplos:

• Gráficos de Dependencia Parcial y de Expectativa Condicional Individual

Notas al pie de página

1

Para la clasificación, la respuesta objetivo puede ser la probabilidad de una clase (la clase positiva para la clasificación binaria), o la función de decisión.

Referencias

T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning, Second Edition, Section 10.13.2, Springer, 2009.

C. Molnar, Interpretable Machine Learning, Section 5.1, 2019.

A. Goldstein, A. Kapelner, J. Bleich, and E. Pitkin, Peeking Inside the Black Box: Visualizing Statistical Learning With Plots of Individual Conditional Expectation, Journal of Computational and Graphical Statistics, 24(1): 44-65, Springer, 2015.