Comparación estadística de modelos utilizando la búsqueda en cuadrícula

Este ejemplo ilustra cómo comparar estadísticamente el rendimiento de los modelos entrenados y evaluados utilizando GridSearchCV.

Empezaremos simulando datos con forma de luna (donde la separación ideal entre clases no es lineal), añadiendo a ello un grado moderado de ruido. Los puntos de datos pertenecerán a una de las dos clases posibles, que serán predichas por dos características. Simularemos 50 muestras para cada clase:

print(__doc__)
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_moons

X, y = make_moons(noise=0.352, random_state=1, n_samples=100)

sns.scatterplot(
    x=X[:, 0], y=X[:, 1], hue=y,
    marker='o', s=25, edgecolor='k', legend=False
).set_title("Data")
plt.show()

Compararemos el rendimiento de los estimadores SVC que varían en su parámetro kernel, para decidir qué elección de este hiperparámetro predice mejor nuestros datos simulados. Evaluaremos el rendimiento de los modelos utilizando RepeatedStratifiedKFold, repitiendo 10 veces una validación cruzada estratificada de 10-pliegues (fold) utilizando una aleatorización diferente de los datos en cada repetición. El rendimiento se evaluará utilizando roc_auc_score.

from sklearn.model_selection import GridSearchCV, RepeatedStratifiedKFold
from sklearn.svm import SVC

param_grid = [
    {'kernel': ['linear']},
    {'kernel': ['poly'], 'degree': [2, 3]},
    {'kernel': ['rbf']}
]

svc = SVC(random_state=0)

cv = RepeatedStratifiedKFold(
    n_splits=10, n_repeats=10, random_state=0
)

search = GridSearchCV(
    estimator=svc, param_grid=param_grid,
    scoring='roc_auc', cv=cv
)
search.fit(X, y)

Out:

GridSearchCV(cv=RepeatedStratifiedKFold(n_repeats=10, n_splits=10, random_state=0),
             estimator=SVC(random_state=0),
             param_grid=[{'kernel': ['linear']},
                         {'degree': [2, 3], 'kernel': ['poly']},
                         {'kernel': ['rbf']}],
             scoring='roc_auc')

Ahora podemos inspeccionar los resultados de nuestra búsqueda, ordenados por su mean_test_score:

import pandas as pd

results_df = pd.DataFrame(search.cv_results_)
results_df = results_df.sort_values(by=['rank_test_score'])
results_df = (
    results_df
    .set_index(results_df["params"].apply(
        lambda x: "_".join(str(val) for val in x.values()))
    )
    .rename_axis('kernel')
)
results_df[
    ['params', 'rank_test_score', 'mean_test_score', 'std_test_score']
]

	params	rank_test_score	mean_test_score	std_test_score
kernel
rbf	{'kernel': 'rbf'}	1	0.9400	0.079297
linear	{'kernel': 'linear'}	2	0.9300	0.077846
3_poly	{'degree': 3, 'kernel': 'poly'}	3	0.9044	0.098776
2_poly	{'degree': 2, 'kernel': 'poly'}	4	0.6852	0.169106

Podemos ver que el estimador que utiliza el kernel «rbf» es el que mejor funciona, seguido de cerca por el 'linear'. Ambos estimadores con un kernel 'poly' se comportaron peor, con el que utiliza un polinomio de segundo grado logrando un rendimiento mucho menor que todos los demás modelos.

Normalmente, el análisis termina aquí, pero falta la mitad de la historia. La salida de GridSearchCV no proporciona información sobre la certeza de las diferencias entre los modelos. No sabemos si son estadísticamente significativas. Para evaluar esto, necesitamos realizar una prueba estadística. En concreto, para contrastar el rendimiento de dos modelos debemos comparar estadísticamente sus puntuaciones AUC. Hay 100 muestras (puntuaciones AUC) para cada modelo, ya que repetimos 10 veces una validación cruzada de 10 pliegues (fold).

Sin embargo, las puntuaciones de los modelos no son independientes: todos los modelos se evalúan en las mismas 100 particiones, lo que aumenta la correlación entre el rendimiento de los modelos. Dado que algunas particiones de los datos pueden hacer que la distinción de las clases sea particularmente fácil o difícil de encontrar para todos los modelos, las puntuaciones de los modelos covarían.

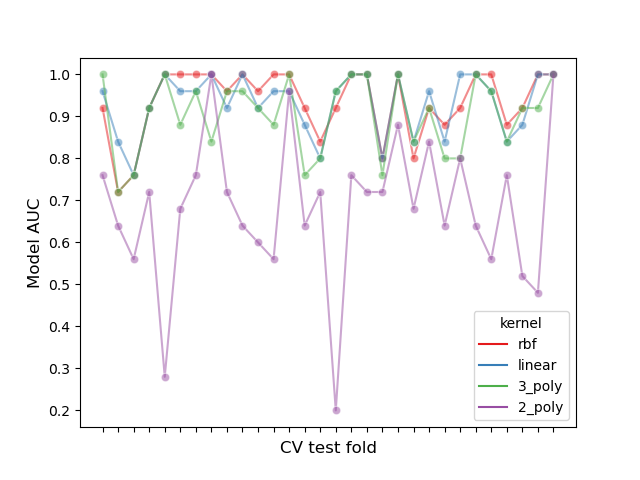
Inspeccionemos este efecto de partición graficando el rendimiento de todos los modelos en cada pliegue y calculando la correlación entre los modelos en todos los pliegues:

# create df of model scores ordered by perfomance
model_scores = results_df.filter(regex=r'split\d*_test_score')

# plot 30 examples of dependency between cv fold and AUC scores
fig, ax = plt.subplots()
sns.lineplot(
    data=model_scores.transpose().iloc[:30],
    dashes=False, palette='Set1', marker='o', alpha=.5, ax=ax
)
ax.set_xlabel("CV test fold", size=12, labelpad=10)
ax.set_ylabel("Model AUC", size=12)
ax.tick_params(bottom=True, labelbottom=False)
plt.show()

# print correlation of AUC scores across folds
print(f"Correlation of models:\n {model_scores.transpose().corr()}")

Out:

Correlation of models:
 kernel       rbf    linear    3_poly    2_poly
kernel
rbf     1.000000  0.882561  0.783392  0.351390
linear  0.882561  1.000000  0.746492  0.298688
3_poly  0.783392  0.746492  1.000000  0.355440
2_poly  0.351390  0.298688  0.355440  1.000000

Podemos observar que el rendimiento de los modelos depende en gran medida del pliegue.

Como consecuencia, si asumimos independencia entre las muestras estaremos subestimando la varianza calculada en nuestras pruebas estadísticas, aumentando el número de errores falsos positivos (es decir, detectar una diferencia significativa entre los modelos cuando esta no existe) 1.

Se han desarrollado varias pruebas estadísticas con corrección de la varianza para estos casos. En este ejemplo mostraremos cómo implementar una de ellas (la llamada prueba t corregida de Nadeau y Bengio) bajo dos enfoques estadísticos diferentes: frecuentista y bayesiano.

Comparando dos modelos: enfoque frecuentista

Podemos empezar preguntando: «¿Es el primer modelo significativamente mejor que el segundo (cuando se clasifica por mean_test_score)?»

Para responder a esta pregunta utilizando un enfoque frecuentista, podríamos ejecutar una prueba t pareada y calcular el valor p. Esto también se conoce como prueba de Diebold-Mariano en la literatura de pronósticos 5. Se han desarrollado muchas variantes de dicha prueba t para tener en cuenta el «problema de la no independencia de las muestras» descrito en la sección anterior. Utilizaremos la que ha demostrado obtener las puntuaciones de replicabilidad más altas (que califica qué tan similar es el rendimiento de un modelo cuando se evalúa en diferentes particiones aleatorias del mismo conjunto de datos), manteniendo al mismo tiempo una tasa baja de falsos positivos y falsos negativos: la prueba t corregida de Nadeau y Bengio 2 que utiliza una validación cruzada de 10-pliegues 10 veces repetida 3.

Esta prueba t pareada corregida se calcula como:

\[t=\frac{\frac{1}{k \cdot r}\sum_{i=1}^{k}\sum_{j=1}^{r}x_{ij}} {\sqrt{(\frac{1}{k \cdot r}+\frac{n_{test}}{n_{train}})\hat{\sigma}^2}}\]

donde \(k\) es el número de pliegues (folds), \(r\) el número de repeticiones en la validación cruzada, \(x\) es la diferencia en el rendimiento de los modelos, \(n_{test}\) es el número de muestras utilizadas para las pruebas, \(n_{train}\) es el número de muestras utilizadas para el entrenamiento, y \(hat{\sigma}^2\) representa la varianza de las diferencias observadas.

Implementemos una prueba t pareada corregida de cola derecha para evaluar si el rendimiento del primer modelo es significativamente mejor que el del segundo. Nuestra hipótesis nula es que el segundo modelo funciona al menos tan bien como el primero.

import numpy as np
from scipy.stats import t


def corrected_std(differences, n_train, n_test):
    """Corrects standard deviation using Nadeau and Bengio's approach.

    Parameters
    ----------
    differences : ndarray of shape (n_samples, 1)
        Vector containing the differences in the score metrics of two models.
    n_train : int
        Number of samples in the training set.
    n_test : int
        Number of samples in the testing set.

    Returns
    -------
    corrected_std : int
        Variance-corrected standard deviation of the set of differences.
    """
    n = n_train + n_test
    corrected_var = (
        np.var(differences, ddof=1) * ((1 / n) + (n_test / n_train))
    )
    corrected_std = np.sqrt(corrected_var)
    return corrected_std


def compute_corrected_ttest(differences, df, n_train, n_test):
    """Computes right-tailed paired t-test with corrected variance.

    Parameters
    ----------
    differences : array-like of shape (n_samples, 1)
        Vector containing the differences in the score metrics of two models.
    df : int
        Degrees of freedom.
    n_train : int
        Number of samples in the training set.
    n_test : int
        Number of samples in the testing set.

    Returns
    -------
    t_stat : float
        Variance-corrected t-statistic.
    p_val : float
        Variance-corrected p-value.
    """
    mean = np.mean(differences)
    std = corrected_std(differences, n_train, n_test)
    t_stat = mean / std
    p_val = t.sf(np.abs(t_stat), df)  # right-tailed t-test
    return t_stat, p_val

model_1_scores = model_scores.iloc[0].values  # scores of the best model
model_2_scores = model_scores.iloc[1].values  # scores of the second-best model

differences = model_1_scores - model_2_scores

n = differences.shape[0]  # number of test sets
df = n - 1
n_train = len(list(cv.split(X, y))[0][0])
n_test = len(list(cv.split(X, y))[0][1])

t_stat, p_val = compute_corrected_ttest(differences, df, n_train, n_test)
print(f"Corrected t-value: {t_stat:.3f}\n"
      f"Corrected p-value: {p_val:.3f}")

Out:

Corrected t-value: 0.750
Corrected p-value: 0.227

Podemos comparar los valores t y p corregidos con los no corregidos:

t_stat_uncorrected = (
    np.mean(differences) / np.sqrt(np.var(differences, ddof=1) / n)
)
p_val_uncorrected = t.sf(np.abs(t_stat_uncorrected), df)

print(f"Uncorrected t-value: {t_stat_uncorrected:.3f}\n"
      f"Uncorrected p-value: {p_val_uncorrected:.3f}")

Out:

Uncorrected t-value: 2.611
Uncorrected p-value: 0.005

Utilizando el nivel de significación alfa convencional a p=0.05, observamos que la prueba t no corregida concluye que el primer modelo es significativamente mejor que el segundo.

En contraste, con el enfoque corregido no detectamos esta diferencia.

En este último caso, sin embargo, el enfoque frecuentista no nos permite concluir que el primer y el segundo modelo tengan un rendimiento equivalente. Si quisiéramos hacer esta afirmación, tendríamos que utilizar un enfoque bayesiano.

Comparando dos modelos: enfoque Bayesiano

Podemos utilizar la estimación bayesiana para calcular la probabilidad de que el primer modelo sea mejor que el segundo. La estimación bayesiana dará como resultado una distribución seguida de la media \(\mu\) de las diferencias en el rendimiento de dos modelos.

Para obtener la distribución posterior tenemos que definir una distribución a priori que modele nuestras creencias sobre cómo se distribuye la media antes de observar los datos, y multiplicarlo por una función de verosimilitud que calcule la probabilidad de nuestras diferencias observadas, dados los valores que podría tomar la media de las diferencias.

La estimación bayesiana puede llevarse a cabo de muchas formas para responder a nuestra pregunta, pero en este ejemplo implementaremos el enfoque sugerido por Benavoli y colegas 4.

Una forma de definir nuestra distribución posterior utilizando una expresión de forma cerrada es seleccionar una distribución a priori conjugada a la función de verosimilitud. Benavoli y sus colegas 4 muestran que cuando se compara el rendimiento de dos clasificadores podemos modelar la a priori como una distribución Normal-Gamma (con media y varianza desconocidas) conjugada con una verosimilitud normal, para así expresar la posterior como una distribución normal. Marginalizando la varianza de esta distribución posterior normal, podemos definir la posterior del parámetro de la media como una distribución t de Student. Específicamente:

\[St(\mu;n-1,\overline{x},(\frac{1}{n}+\frac{n_{test}}{n_{train}}) \hat{\sigma}^2)\]

donde \(n\) es el número total de muestras, \(overline{x}\) representa la diferencia media de las puntuaciones, \(n_{test}\) es el número de muestras utilizadas para las pruebas, \(n_{train}\) es el número de muestras utilizadas para el entrenamiento, y \(hat{\sigma}^2\) representa la varianza de las diferencias observadas.

Ten en cuenta que también utilizamos la varianza corregida de Nadeau y Bengio en nuestro enfoque bayesiano.

Calculemos y grafiquemos la distribución posterior:

# intitialize random variable
t_post = t(
    df, loc=np.mean(differences),
    scale=corrected_std(differences, n_train, n_test)
)

Vamos a graficar la distribución posterior:

x = np.linspace(t_post.ppf(0.001), t_post.ppf(0.999), 100)

plt.plot(x, t_post.pdf(x))
plt.xticks(np.arange(-0.04, 0.06, 0.01))
plt.fill_between(x, t_post.pdf(x), 0, facecolor='blue', alpha=.2)
plt.ylabel("Probability density")
plt.xlabel(r"Mean difference ($\mu$)")
plt.title("Posterior distribution")
plt.show()

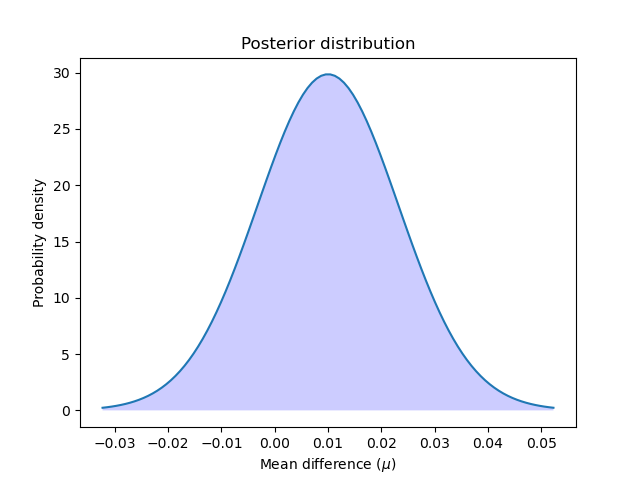
Podemos calcular la probabilidad de que el primer modelo sea mejor que el segundo calculando el área bajo la curva de la distribución posterior de cero a infinito. Y también a la inversa: podemos calcular la probabilidad de que el segundo modelo sea mejor que el primero calculando el área bajo la curva de menos infinito a cero.

better_prob = 1 - t_post.cdf(0)

print(f"Probability of {model_scores.index[0]} being more accurate than "
      f"{model_scores.index[1]}: {better_prob:.3f}")
print(f"Probability of {model_scores.index[1]} being more accurate than "
      f"{model_scores.index[0]}: {1 - better_prob:.3f}")

Out:

Probability of rbf being more accurate than linear: 0.773
Probability of linear being more accurate than rbf: 0.227

En contraste con el enfoque frecuentista, podemos calcular la probabilidad de que un modelo sea mejor que el otro.

Ten en cuenta que obtuvimos resultados similares a los del enfoque frecuentista. Dada nuestra elección de las distribuciones a priori, estamos realizando esencialmente los mismos cálculos, pero podemos hacer diferentes afirmaciones.

Región de equivalencia práctica

A veces nos interesa determinar las probabilidades de que nuestros modelos tengan un rendimiento equivalente, donde «equivalente» se define de forma práctica. Un enfoque ingenuo 4 sería definir los estimadores como prácticamente equivalentes cuando difieren en menos de un 1% en su exactitud. Pero también podríamos definir esta equivalencia práctica teniendo en cuenta el problema que intentamos resolver. Por ejemplo, una diferencia del 5% en la exactitud significaría un aumento de 1.000$ en las ventas, y consideramos que cualquier cantidad superior a esa es relevante para nuestro negocio.

En este ejemplo vamos a definir la Región de Equivalencia Práctica (ROPE) como \([-0.01, 0.01]\). Es decir, consideraremos que dos modelos son prácticamente equivalentes si difieren en menos de un 1% en su rendimiento.

Para calcular las probabilidades de que los clasificadores sean prácticamente equivalentes, calculamos el área bajo la curva de la distribución posterior sobre el intervalo ROPE:

rope_interval = [-0.01, 0.01]
rope_prob = t_post.cdf(rope_interval[1]) - t_post.cdf(rope_interval[0])

print(f"Probability of {model_scores.index[0]} and {model_scores.index[1]} "
      f"being practically equivalent: {rope_prob:.3f}")

Out:

Probability of rbf and linear being practically equivalent: 0.432

Podemos graficar cómo se distribuye la posterior sobre el intervalo ROPE:

x_rope = np.linspace(rope_interval[0], rope_interval[1], 100)

plt.plot(x, t_post.pdf(x))
plt.xticks(np.arange(-0.04, 0.06, 0.01))
plt.vlines([-0.01, 0.01], ymin=0, ymax=(np.max(t_post.pdf(x)) + 1))
plt.fill_between(x_rope, t_post.pdf(x_rope), 0, facecolor='blue', alpha=.2)
plt.ylabel("Probability density")
plt.xlabel(r"Mean difference ($\mu$)")
plt.title("Posterior distribution under the ROPE")
plt.show()

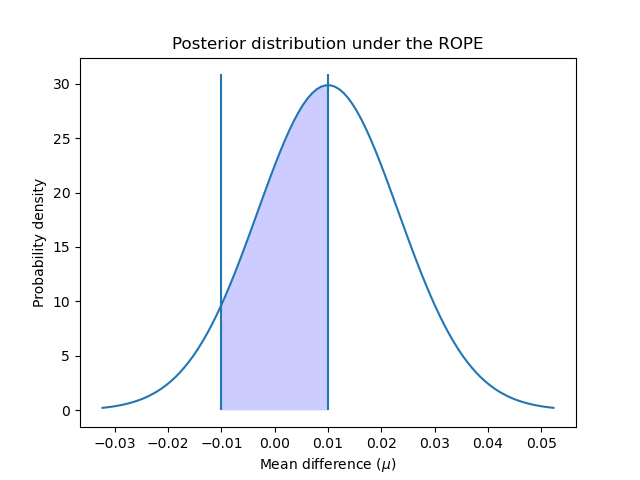
Como se sugiere en 4, podemos seguir interpretando estas probabilidades utilizando los mismos criterios que el enfoque frecuentista: ¿es la probabilidad de caer dentro del ROPE mayor del 95% (valor alfa del 5%)? En ese caso, podemos concluir que ambos modelos son prácticamente equivalentes.

El enfoque de la estimación bayesiana también nos permite calcular el grado de incertidumbre de nuestra estimación de la diferencia. Esto puede calcularse utilizando intervalos de credibilidad. Para una probabilidad dada, muestran el rango de valores que puede tomar la cantidad estimada, en nuestro caso la diferencia media de rendimiento. Por ejemplo, un intervalo de credibilidad del 50% [x, y] nos dice que hay un 50% de probabilidad de que la verdadera (media) diferencia de rendimiento entre los modelos esté entre x e y.

Vamos a determinar los intervalos de credibilidad de nuestros datos utilizando el 50%, el 75% y el 95%:

cred_intervals = []
intervals = [0.5, 0.75, 0.95]

for interval in intervals:
    cred_interval = list(t_post.interval(interval))
    cred_intervals.append([interval, cred_interval[0], cred_interval[1]])

cred_int_df = pd.DataFrame(
    cred_intervals,
    columns=['interval', 'lower value', 'upper value']
).set_index('interval')
cred_int_df

	lower value	upper value
interval
0.50	0.000977	0.019023
0.75	-0.005422	0.025422
0.95	-0.016445	0.036445

Como se muestra en la tabla, hay un 50% de probabilidad de que la verdadera diferencia media entre los modelos esté entre 0.000977 y 0.019023, un 70% de probabilidad de que esté entre -0.005422 y 0.025422, y un 95% de probabilidad de que esté entre -0.016445 y 0.036445.

Comparación por pares de todos los modelos: enfoque frecuentista

También podríamos estar interesados en comparar el rendimiento de todos nuestros modelos evaluados con GridSearchCV. En este caso estaríamos ejecutando nuestra prueba estadística múltiples veces, lo que nos lleva al problema de las comparaciones múltiples.

Hay muchas formas posibles de abordar este problema, pero un enfoque estándar es aplicar una corrección de Bonferroni. El Bonferroni se puede calcular multiplicando el valor p por el número de comparaciones que estamos probando.

Comparemos el rendimiento de los modelos utilizando la prueba t corregida:

from itertools import combinations
from math import factorial

n_comparisons = (
    factorial(len(model_scores))
    / (factorial(2) * factorial(len(model_scores) - 2))
)
pairwise_t_test = []

for model_i, model_k in combinations(range(len(model_scores)), 2):
    model_i_scores = model_scores.iloc[model_i].values
    model_k_scores = model_scores.iloc[model_k].values
    differences = model_i_scores - model_k_scores
    t_stat, p_val = compute_corrected_ttest(
        differences, df, n_train, n_test
    )
    p_val *= n_comparisons  # implement Bonferroni correction
    # Bonferroni can output p-values higher than 1
    p_val = 1 if p_val > 1 else p_val
    pairwise_t_test.append(
        [model_scores.index[model_i], model_scores.index[model_k],
         t_stat, p_val]
    )

pairwise_comp_df = pd.DataFrame(
    pairwise_t_test,
    columns=['model_1', 'model_2', 't_stat', 'p_val']
).round(3)
pairwise_comp_df

	model_1	model_2	t_stat	p_val
0	rbf	linear	0.750	1.000
1	rbf	3_poly	1.657	0.302
2	rbf	2_poly	4.565	0.000
3	linear	3_poly	1.111	0.807
4	linear	2_poly	4.276	0.000
5	3_poly	2_poly	3.851	0.001

Observamos que, tras corregir las comparaciones múltiples, el único modelo que difiere significativamente de los demás es '2_poly'. 'rbf', el modelo clasificado en primer lugar por GridSearchCV, no difiere significativamente de 'linear' o '3_poly'.

Comparación por pares de todos los modelos: Enfoque bayesiano

Cuando se utiliza la estimación bayesiana para comparar múltiples modelos, no es necesario corregir las comparaciones múltiples (para saber por qué, consulta 4).

Podemos realizar nuestras comparaciones por pares de la misma manera que en la primera sección:

pairwise_bayesian = []

for model_i, model_k in combinations(range(len(model_scores)), 2):
    model_i_scores = model_scores.iloc[model_i].values
    model_k_scores = model_scores.iloc[model_k].values
    differences = model_i_scores - model_k_scores
    t_post = t(
        df, loc=np.mean(differences),
        scale=corrected_std(differences, n_train, n_test)
    )
    worse_prob = t_post.cdf(rope_interval[0])
    better_prob = 1 - t_post.cdf(rope_interval[1])
    rope_prob = t_post.cdf(rope_interval[1]) - t_post.cdf(rope_interval[0])

    pairwise_bayesian.append([worse_prob, better_prob, rope_prob])

pairwise_bayesian_df = (pd.DataFrame(
    pairwise_bayesian,
    columns=['worse_prob', 'better_prob', 'rope_prob']
).round(3))

pairwise_comp_df = pairwise_comp_df.join(pairwise_bayesian_df)
pairwise_comp_df

	model_1	model_2	t_stat	p_val	worse_prob	better_prob	rope_prob
0	rbf	linear	0.750	1.000	0.068	0.500	0.432
1	rbf	3_poly	1.657	0.302	0.018	0.882	0.100
2	rbf	2_poly	4.565	0.000	0.000	1.000	0.000
3	linear	3_poly	1.111	0.807	0.063	0.750	0.187
4	linear	2_poly	4.276	0.000	0.000	1.000	0.000
5	3_poly	2_poly	3.851	0.001	0.000	1.000	0.000

Utilizando el enfoque bayesiano podemos calcular la probabilidad de que un modelo tenga un rendimiento mejor, peor o prácticamente equivalente a otro.

Los resultados muestran que el modelo clasificado en primer lugar por GridSearchCV 'rbf', tiene aproximadamente un 6.8% de incertidumbre (chance) de ser peor que 'linear', y un 1.8% de incertidumbre de ser peor que '3_poly'. 'rbf' y 'linear' tienen un 43% de probabilidad de ser prácticamente equivalentes, mientras que 'rbf' y '3_poly' tienen un 10% de probabilidad de serlo.

Al igual que las conclusiones obtenidas con el enfoque frecuentista, todos los modelos tienen una probabilidad del 100% de ser mejores que '2_poly', y ninguno tiene un rendimiento prácticamente equivalente con este último.

Mensajes para llevar a casa

• Las pequeñas diferencias en las medidas de rendimiento pueden resultar fácilmente ser mera casualidad, pero no porque un modelo prediga sistemáticamente mejor que el otro. Como se muestra en este ejemplo, las estadísticas pueden indicar la probabilidad de que eso ocurra.

• Al comparar estadísticamente el rendimiento de dos modelos evaluados en GridSearchCV, es necesario corregir la varianza calculada, que podría estar subestimada, ya que las puntuaciones de los modelos no son independientes entre sí.

• Un enfoque frecuentista que utiliza una prueba t pareada (con corrección de la varianza) puede decirnos si el rendimiento de un modelo es mejor que el de otro con un grado de certeza superior al del azar.

• Un enfoque bayesiano puede proporcionar las probabilidades de que un modelo sea mejor, peor o prácticamente equivalente a otro. También puede indicarnos el grado de confianza que tenemos para saber que las verdaderas diferencias de nuestros modelos se encuentran bajo un determinado rango de valores.

• Si se comparan estadísticamente múltiples modelos, se necesita una corrección de comparaciones múltiples cuando se utiliza el enfoque frecuentista.

Referencias

1

Dietterich, T. G. (1998). Approximate statistical tests for comparing supervised classification learning algorithms. Neural computation, 10(7).

2

Nadeau, C., y Bengio, Y. (2000). Inference for the generalization error. In Advances in neural information processing systems.

3

Bouckaert, R. R., y Frank, E. (2004). Evaluating the replicability of significance tests for comparing learning algorithms. In Pacific-Asia Conference on Knowledge Discovery and Data Mining.

4(1,2,3,4,5)

Benavoli, A., Corani, G., Demšar, J., y Zaffalon, M. (2017). Time for a change: a tutorial for comparing multiple classifiers through Bayesian analysis. The Journal of Machine Learning Research, 18(1). Consulta la biblioteca de Python que acompaña a este documento aquí.

5

Diebold, F.X. y Mariano R.S. (1995). Comparing predictive accuracy Journal of Business & economic statistics, 20(1), 134-144.