6.7. Aproximación de núcleo¶

Este submódulo contiene funciones que aproximan los mapeos de características que corresponden a ciertos núcleos (kernels), tal y como se utilizan, por ejemplo, en las máquinas de vectores de soporte (véase Máquinas de Vectores de Soporte). Las siguientes funciones de características realizan transformaciones no lineales de la entrada, que pueden servir de base para la clasificación lineal u otros algoritmos.

La ventaja de utilizar mapas de características explícitas (explicit feature maps) aproximados en comparación con el truco del núcleo kernel trick, que hace uso de los mapas de características de forma implícita, es que los mapeos explícitos pueden ser más adecuados para el aprendizaje en línea (online learning) y pueden reducir significativamente el coste del aprendizaje con conjuntos de datos muy grandes. Las SVM de núcleo estándar no se escalan bien en grandes conjuntos de datos, pero utilizando un mapa de núcleo aproximado es posible utilizar SVM lineales mucho más eficientes. En particular, la combinación de aproximaciones del mapa del núcleo con SGDClassifier puede hacer posible el aprendizaje no lineal en grandes conjuntos de datos.

Dado que no se han realizado muchos trabajos empíricos utilizando embeddings aproximados, es aconsejable comparar los resultados con los métodos de núcleos exactos cuando sea posible.

Ver también

Regresión polinómica: ampliación de los modelos lineales con funciones de base para una transformación polinómica exacta.

6.7.1. Método Nystroem para la aproximación de núcleos¶

El método Nystroem, tal y como se implementa en Nystroem es un método general para aproximaciones de bajo nivel de los núcleos. Lo consigue esencialmente mediante el submuestreo de los datos sobre los que se evalúa el núcleo. Por defecto, Nystroem utiliza el kernel rbf, pero puede utilizar cualquier función del kernel o una matriz del kernel precalculada. El número de muestras utilizadas - que es también la dimensionalidad de las características calculadas - viene dado por el parámetro n_components.

6.7.2. Núcleo de la función de base radial¶

La RBFSampler construye un mapeo aproximado para el núcleo de la función de base radial (radial basis function kernel, RBF), también conocido como Random Kitchen Sinks [RR2007]. Esta transformación puede utilizarse para modelar explícitamente un mapa de núcleo, antes de aplicar un algoritmo lineal, por ejemplo una SVM lineal:

>>> from sklearn.kernel_approximation import RBFSampler
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> rbf_feature = RBFSampler(gamma=1, random_state=1)
>>> X_features = rbf_feature.fit_transform(X)
>>> clf = SGDClassifier(max_iter=5)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=5)
>>> clf.score(X_features, y)
1.0

El mapeo se basa en una aproximación de Monte Carlo a los valores del núcleo. La función fit realiza el muestreo de Monte Carlo, mientras que el método transform realiza el mapeo de los datos. Debido a la aleatoriedad inherente al proceso, los resultados pueden variar entre diferentes llamadas a la función fit.

La función fit toma dos argumentos: n_components, que es la dimensionalidad objetivo de la transformación de características, y gamma, el parámetro del núcleo RBF. Un n_components más alto dará lugar a una mejor aproximación del núcleo y producirá resultados más similares a los producidos por un núcleo SVM. Ten en cuenta que el «ajuste» de la función característica no depende realmente de los datos dados a la función fit. Sólo se utiliza la dimensionalidad de los datos. Los detalles del método se pueden encontrar en [RR2007].

Para un valor determinado de n_components RBFSampler suele ser menos preciso que Nystroem. Sin embargo, RBFSampler es menos costoso de calcular, lo que hace más eficiente el uso de espacios de características más grandes.

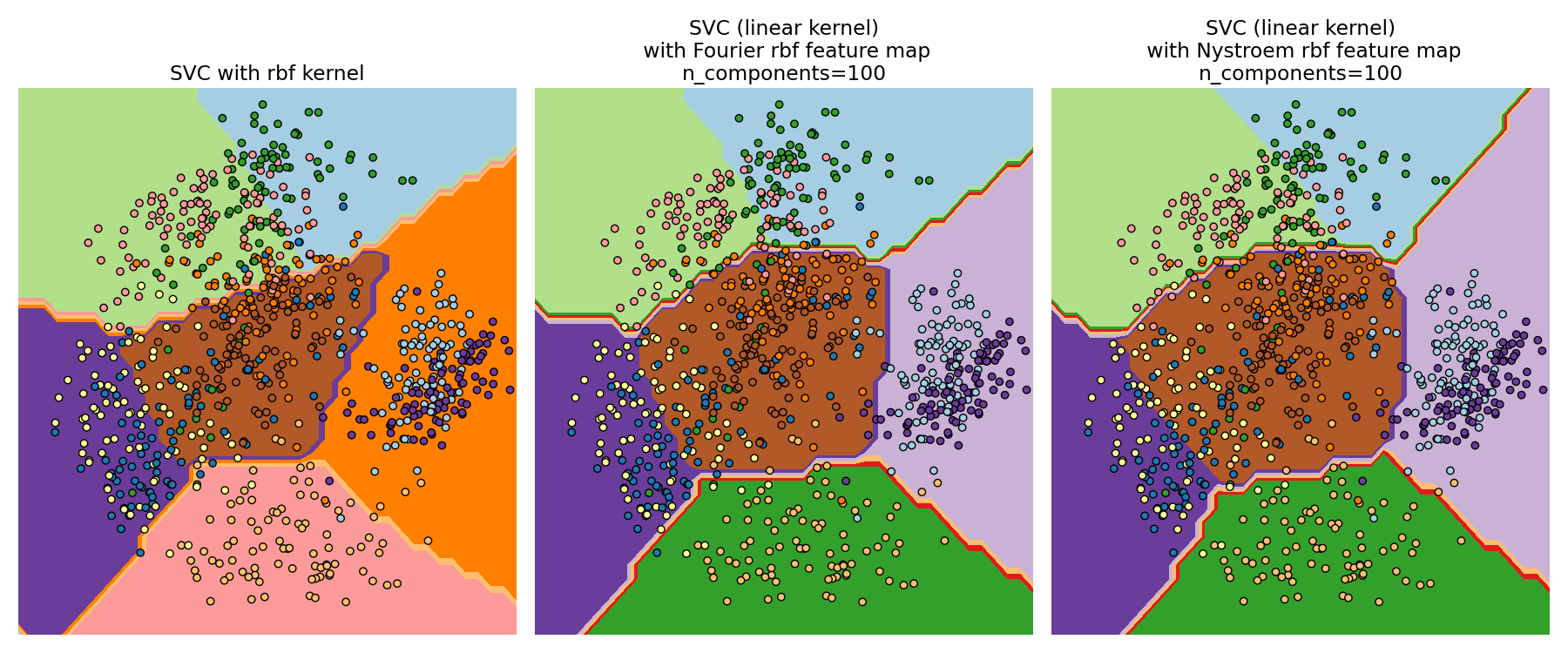
../_images/sphx_glr_plot_kernel_approximation_002.png — Comparación de un núcleo RBF exacto (izquierda) con la aproximación (derecha)¶

Ejemplos:

Aproximación explícita del mapeo de características para los núcleos RBF

6.7.3. Núcleo aditivo de chi cuadrado¶

El núcleo chi cuadrado aditivo es un núcleo basado en histogramas que se utiliza a menudo en la visión por computadora.

El núcleo aditivo de chi-cuadrado utilizado aquí viene dado por

\[k(x, y) = \sum_i \frac{2x_iy_i}{x_i+y_i}\]

Esto no es exactamente lo mismo que sklearn.metrics.additive_chi2_kernel. Los autores de [VZ2010] prefieren la versión anterior ya que siempre es definida positiva. Como el núcleo es aditivo, es posible tratar todos los componentes \(x_i\) por separado para la incrustación (embedding). Esto hace posible muestrear la transformada de Fourier en intervalos regulares, en lugar de aproximar utilizando el muestreo de Monte Carlo.

La clase AdditiveChi2Sampler implementa este muestreo determinista por componentes. Cada componente se muestrea \(n\) veces, dando lugar a \(2n+1\) dimensiones por dimensión de entrada (el múltiplo de dos proviene de la parte real y compleja de la transformada de Fourier). En la bibliografía, \(n\) suele elegirse como 1 o 2, lo que transforma el conjunto de datos en un tamaño de n_samples * 5 * n_features (en el caso de \(n=2\)).

El mapa de características aproximado proporcionado por AdditiveChi2Sampler puede combinarse con el mapa de características aproximado proporcionado por RBFSampler para obtener un mapa de características aproximado para el núcleo de chi cuadrado exponenciado. Ver el documento [VZ2010] para más detalles y [VVZ2010] para la combinación con la RBFSampler.

6.7.4. Núcleo de chi cuadrado sesgado¶

El núcleo de chi cuadrado sesgado viene dado por:

\[k(x,y) = \prod_i \frac{2\sqrt{x_i+c}\sqrt{y_i+c}}{x_i + y_i + 2c}\]

Tiene propiedades similares al núcleo de chi cuadrado exponenciado que se utiliza a menudo en la visión por computadora, pero permite una aproximación simple de Monte Carlo del mapa de características.

El uso del SkewedChi2Sampler es el mismo que el descrito anteriormente para el RBFSampler. La única diferencia está en el parámetro independiente, que se llama \(c\). Para conocer la motivación de este mapeo y los detalles matemáticos, ver [LS2010].

6.7.5. Aproximación de núcleos polinómicos a través de Tensor Sketch¶

El núcleo polinómico es un tipo popular de función de núcleo dada por:

\[k(x, y) = (\gamma x^\top y +c_0)^d\]

donde:

x, y son los vectores de entrada

d es el grado (degree) del núcleo

Intuitivamente, el espacio de características del kernel polinomial de grado d consiste en todos los posibles productos de grado d entre las características de entrada, lo que permite a los algoritmos de aprendizaje que utilizan este kernel tener en cuenta las interacciones entre las características.

El método TensorSketch [PP2013], implementado en PolynomialCountSketch, es un método escalable e independiente de los datos de entrada para la aproximación de núcleos polinómicos. Se basa en el concepto de Count Sketch [WIKICS] [CCF2002] , una técnica de reducción de la dimensionalidad similar al feature hashing, que en cambio utiliza varias funciones hash independientes. TensorSketch obtiene un Count Sketch del producto exterior (outer product) de dos vectores (o de un vector consigo mismo), que puede utilizarse como una aproximación del espacio de características del núcleo polinómico. En concreto, en lugar de calcular explícitamente el producto exterior, TensorSketch calcula el Count Sketch de los vectores y luego utiliza la multiplicación polinómica a través de la Transformada Rápida de Fourier para calcular el Count Sketch de su producto exterior.

Convenientemente, la fase de entrenamiento de TensorSketch consiste simplemente en inicializar algunas variables aleatorias. Por tanto, es independiente de los datos de entrada, es decir, solo depende del número de características de entrada, pero no de los valores de los datos. Además, este método puede transformar muestras en tiempo \(\mathcal{O}(n_{\text{samples}}(n_{\text{features}} + n_{\text{components}} \log(n_{\text{components}})))\), donde \(n_{\text{components}}\) es la dimensión de salida deseada, determinada por n_components.

Ejemplos:

Aprendizaje escalable con aproximación del núcleo polinomial

6.7.6. Detalles matemáticos¶

Los métodos de núcleo, como las máquinas de vectores soporte o el PCA «kernelizado», se basan en una propiedad de reproducción de los espacios de Hilbert del núcleo. Para cualquier función de núcleo definida positiva \(k\) (también llamada núcleo de Mercer), se garantiza que existe un mapeo \(\phi\) en un espacio de Hilbert \(\mathcal{H}\), tal que

\[k(x,y) = \langle \phi(x), \phi(y) \rangle\]

Donde \(\langle \cdot, \cdot \rangle\) indica el producto interno en el espacio Hilbert.

Si un algoritmo, tal como una máquina de vectores de soporte lineal o PCA, se basa sólo en el producto escalar de los puntos de datos \(x_i\), se puede utilizar el valor de \(k(x_i, x_j)\), que corresponde a la aplicación del algoritmo a los puntos de datos mapeados \(\phi(x_i)\). La ventaja de utilizar \(k\) es que el mapeo \(\phi\) nunca tiene que ser calculado explícitamente, lo que permite características de tamaño arbitrario (incluso infinito).

Una desventaja de los métodos de núcleo es que puede ser necesario almacenar muchos valores de núcleo \(k(x_i, x_j)\) durante la optimización. Si un clasificador «kernelizado» se aplica a nuevos datos \(y_j\), es necesario calcular \(k(x_i, y_j)\) para hacer predicciones, posiblemente para muchos \(x_i\) diferentes en el conjunto de entrenamiento.

Las clases de este submódulo permiten aproximar el embedding \(\phi\), trabajando así explícitamente con las representaciones \(\phi(x_i)\), lo que evita la necesidad de aplicar el núcleo o almacenar ejemplos de entrenamiento.

Referencias:

RR2007(1,2): «Random features for large-scale kernel machines» Rahimi, A. and Recht, B. - Advances in neural information processing 2007,
LS2010: «Random Fourier approximations for skewed multiplicative histogram kernels» Random Fourier approximations for skewed multiplicative histogram kernels - Lecture Notes for Computer Sciencd (DAGM)
VZ2010(1,2): «Efficient additive kernels via explicit feature maps» Vedaldi, A. and Zisserman, A. - Computer Vision and Pattern Recognition 2010
VVZ2010: «Generalized RBF feature maps for Efficient Detection» Vempati, S. and Vedaldi, A. and Zisserman, A. and Jawahar, CV - 2010
PP2013: «Fast and scalable polynomial kernels via explicit feature maps» Pham, N., & Pagh, R. - 2013
CCF2002: «Finding frequent items in data streams» Charikar, M., Chen, K., & Farach-Colton - 2002
WIKICS: «Wikipedia: Count sketch»