6.6. Proyección aleatoria

El módulo sklearn.random_projection implementa una forma simple y computacionalmente eficiente de reducir la dimensionalidad de los datos intercambiando una cantidad controlada de precisión (como varianza adicional) por tiempos de procesamiento más rápidos y tamaños de modelos más pequeños. Este módulo implementa dos tipos de matrices aleatorias no estructuradas: matriz aleatoria Gaussiana y matriz aleatoria dispersa.

Las dimensiones y distribución de las matrices de proyecciones aleatorias se controlan para preservar las distancias por pares entre dos muestras cualesquiera del conjunto de datos. Así, la proyección aleatoria es una técnica de aproximación adecuada para el método basado en la distancia.

Referencias:

6.6.1. El lema Johnson-Lindenstrauss

El principal resultado teórico detrás de la eficiencia de la proyección aleatoria es el Lema de Johnson-Lindenstrauss (citando a Wikipedia):

En matemáticas, el lema Johnson-Lindenstrauss es un resultado concerniente a las inserciones de baja distorsión de puntos de un espacio de alta dimensión en un espacio euclideano de baja dimensión. El lema afirma que un pequeño conjunto de puntos en un espacio de alta dimensión puede integrarse en un espacio de dimensión mucho más baja de tal manera que las distancias entre los puntos casi se conservan. El mapa utilizado para la inserción es al menos Lipschitz, e incluso puede tomarse como una proyección ortogonal.

Conociendo sólo el número de muestras, la función johnson_lindenstrauss_min_dim estima de forma conservadora el tamaño mínimo del subespacio aleatorio para garantizar una distorsión acotada introducida por la proyección aleatoria:

>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
663
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([    663,   11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894,  9868, 11841])
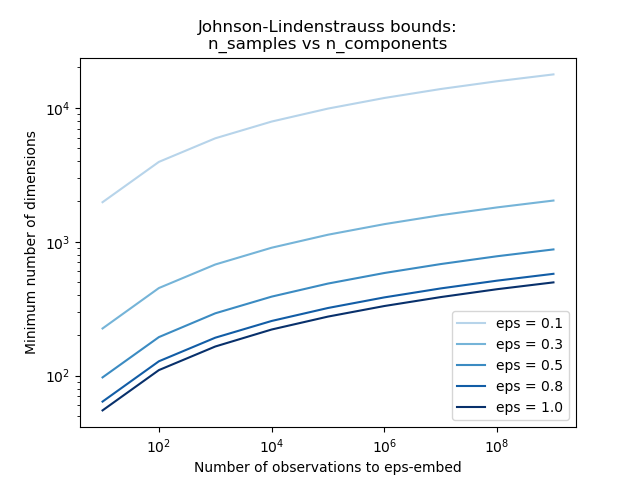
../_images/sphx_glr_plot_johnson_lindenstrauss_bound_001.png
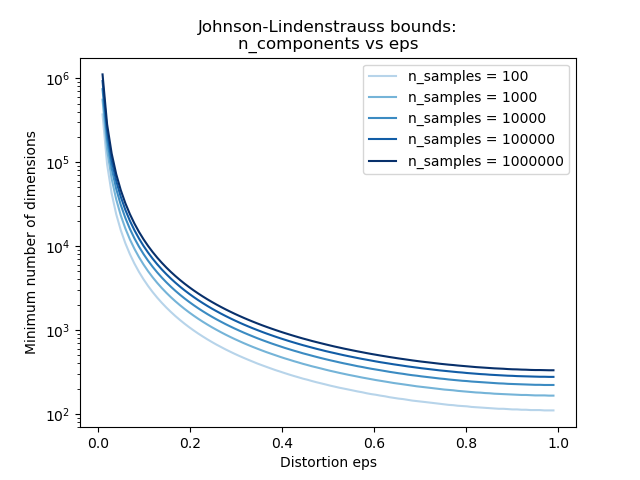
../_images/sphx_glr_plot_johnson_lindenstrauss_bound_002.png

Example:

Referencias:

6.6.2. Proyección aleatoria Gaussiana

La clase GaussianRandomProjection reduce la dimensionalidad proyectando el espacio de entrada original en una matriz generada aleatoriamente donde los componentes se extraen de la siguiente distribución \(N(0, \frac{1}{n_{components}})\).

Aquí un pequeño extracto que ilustra cómo utilizar el transformador de proyección aleatoria Gaussiana:

>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)

6.6.3. Proyección aleatoria dispersa

La clase SparseRandomProjection reduce la dimensionalidad proyectando el espacio de entrada original usando una matriz aleatoria dispersa.

Las matrices aleatorias dispersas son una alternativa a la densa matriz de proyección aleatoria gaussiana que garantiza una calidad de inserción similar, a la vez que es mucho más eficiente en términos de memoria y permite un cálculo más rápido de los datos proyectados.

Si definimos s = 1 / density, los elementos de la matriz aleatoria se extraen de

\[\begin{split}\left\{ \begin{array}{c c l} -\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\ 0 &\text{with probability} & 1 - 1 / s \\ +\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\ \end{array} \right.\end{split}\]

donde \(n_{\text{components}}\) es el tamaño del subespacio proyectado. Por defecto, la densidad de los elementos distintos de cero se establece en la densidad mínima recomendada por Ping Li et al. \(1 / \sqrt{n_{\text{features}}}\).

Aquí un pequeño extracto que ilustra cómo utilizar el transformador de proyección aleatoria dispersa:

>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)

Referencias: