El límite de Johnson-Lindenstrauss para la incrustación con proyecciones aleatorias

El Johnson-Lindenstrauss lemma afirma que cualquier conjunto de datos de alta dimensión puede proyectarse aleatoriamente en un espacio Euclidiano de menor dimensión controlando la distorsión en las distancias por pares.

print(__doc__)

import sys
from time import time
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn.random_projection import johnson_lindenstrauss_min_dim
from sklearn.random_projection import SparseRandomProjection
from sklearn.datasets import fetch_20newsgroups_vectorized
from sklearn.datasets import load_digits
from sklearn.metrics.pairwise import euclidean_distances
from sklearn.utils.fixes import parse_version

# `normed` is being deprecated in favor of `density` in histograms
if parse_version(matplotlib.__version__) >= parse_version('2.1'):
    density_param = {'density': True}
else:
    density_param = {'normed': True}

Límites teóricos

La distorsión introducida por una proyección aleatoria p se afirma por el hecho de que p está definiendo una incrustación eps con buena probabilidad como se define por:

\[(1 - eps) \|u - v\|^2 < \|p(u) - p(v)\|^2 < (1 + eps) \|u - v\|^2\]

Donde u y v son cualquier fila tomada de un conjunto de datos de forma (n_samples, n_features) y p es una proyección de una matriz Gaussiana aleatoria N(0, 1) de forma (n_components, n_features) (o una matriz Achlioptas dispersa).

El número mínimo de componentes para garantizar la incrustación eps viene dado por:

\[n\_components \geq 4 log(n\_samples) / (eps^2 / 2 - eps^3 / 3)\]

El primer gráfico muestra que con un número creciente de muestras n_samples, el número mínimo de dimensiones n_components aumenta logarítmicamente para garantizar una incrustación eps.

# range of admissible distortions
eps_range = np.linspace(0.1, 0.99, 5)
colors = plt.cm.Blues(np.linspace(0.3, 1.0, len(eps_range)))

# range of number of samples (observation) to embed
n_samples_range = np.logspace(1, 9, 9)

plt.figure()
for eps, color in zip(eps_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples_range, eps=eps)
    plt.loglog(n_samples_range, min_n_components, color=color)

plt.legend(["eps = %0.1f" % eps for eps in eps_range], loc="lower right")
plt.xlabel("Number of observations to eps-embed")
plt.ylabel("Minimum number of dimensions")
plt.title("Johnson-Lindenstrauss bounds:\nn_samples vs n_components")
plt.show()

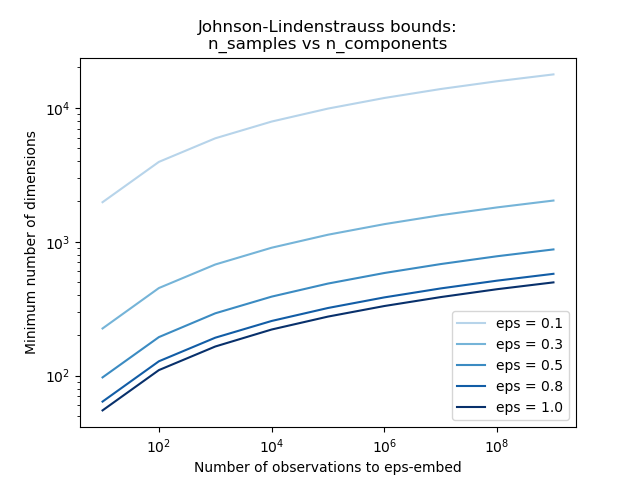
El segundo gráfico muestra que un aumento de la distorsión admisible eps permite reducir drásticamente el número mínimo de dimensiones n_components para un número determinado de muestras n_samples

# range of admissible distortions
eps_range = np.linspace(0.01, 0.99, 100)

# range of number of samples (observation) to embed
n_samples_range = np.logspace(2, 6, 5)
colors = plt.cm.Blues(np.linspace(0.3, 1.0, len(n_samples_range)))

plt.figure()
for n_samples, color in zip(n_samples_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples, eps=eps_range)
    plt.semilogy(eps_range, min_n_components, color=color)

plt.legend(["n_samples = %d" % n for n in n_samples_range], loc="upper right")
plt.xlabel("Distortion eps")
plt.ylabel("Minimum number of dimensions")
plt.title("Johnson-Lindenstrauss bounds:\nn_components vs eps")
plt.show()

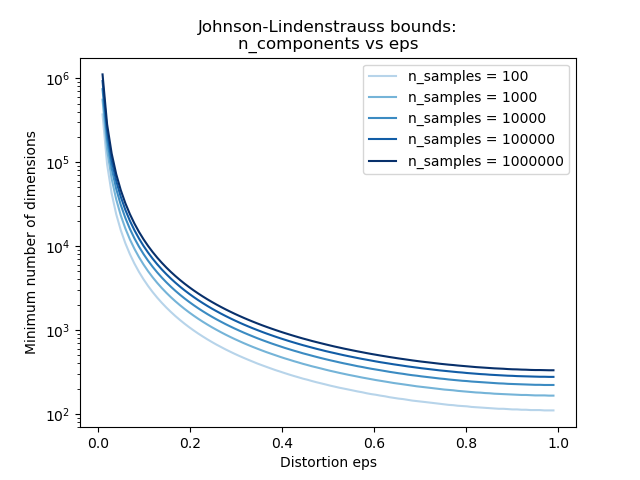
Validación empírica

Validamos los límites anteriores en el conjunto de datos del documento de texto de 20 grupos de noticias (frecuencias de palabras TF-IDF) o en el conjunto de datos de dígitos:

• para el conjunto de datos de 20 grupos de noticias se proyectan unos 500 documentos con 100k características en total utilizando una matriz aleatoria dispersa a espacios euclidianos más pequeños con varios valores para el número de dimensiones objetivo n_components.

• para el conjunto de datos de dígitos, algunos datos de píxeles de nivel de gris de 8x8 para 500 imágenes de dígitos escritos a mano se proyectan aleatoriamente en espacios para varios números mayores de dimensiones n_components.

El conjunto de datos predeterminados es el conjunto de datos de 20 grupos de noticias. Para ejecutar el ejemplo en el conjunto de datos de dígitos, pasa el argumento de línea de comandos --use-digits-dataset a este script.

if '--use-digits-dataset' in sys.argv:
    data = load_digits().data[:500]
else:
    data = fetch_20newsgroups_vectorized().data[:500]

Para cada valor de n_components, graficamos:

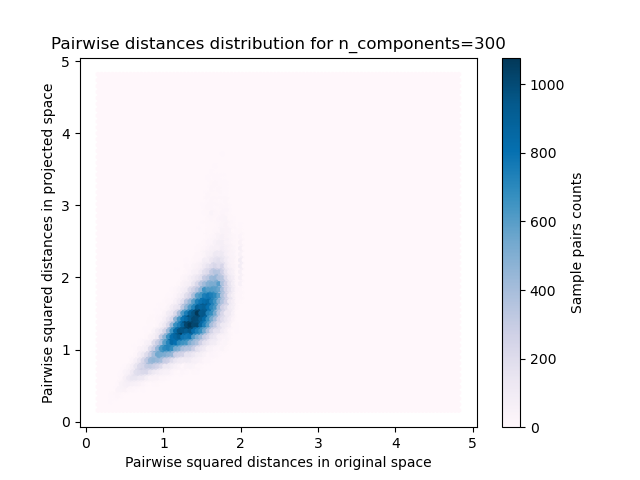
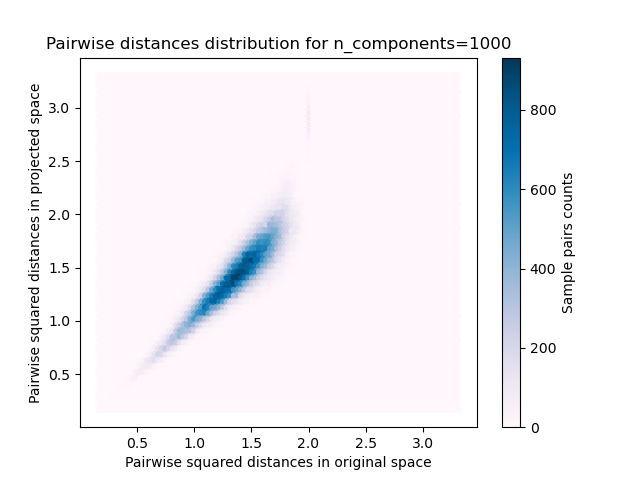
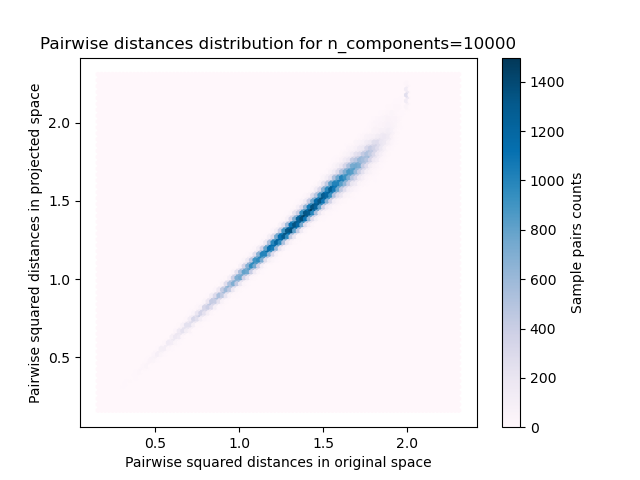
• Distribución 2D de los pares de muestras con las distancias por pares en los espacios original y proyectado como ejes x e y respectivamente.

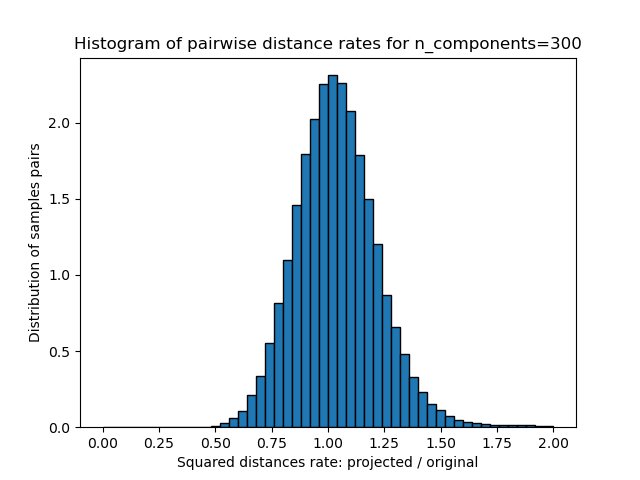
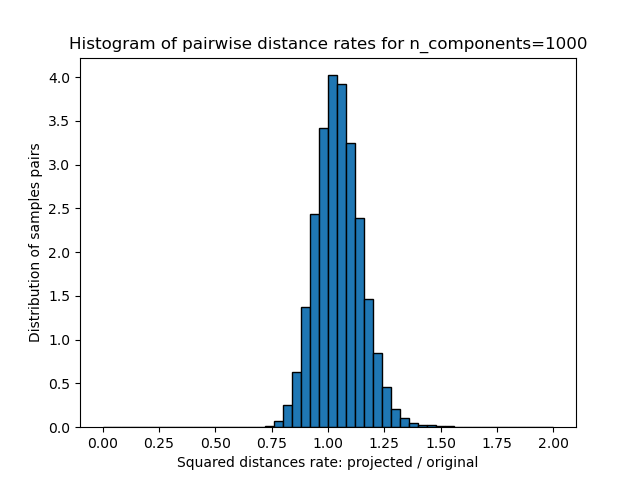
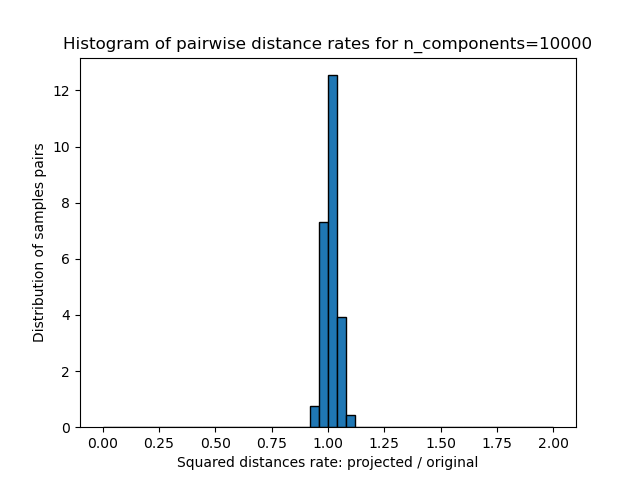
• Histograma 1D de la razón de esas distancias (proyectada / original).

n_samples, n_features = data.shape
print("Embedding %d samples with dim %d using various random projections"
      % (n_samples, n_features))

n_components_range = np.array([300, 1000, 10000])
dists = euclidean_distances(data, squared=True).ravel()

# select only non-identical samples pairs
nonzero = dists != 0
dists = dists[nonzero]

for n_components in n_components_range:
    t0 = time()
    rp = SparseRandomProjection(n_components=n_components)
    projected_data = rp.fit_transform(data)
    print("Projected %d samples from %d to %d in %0.3fs"
          % (n_samples, n_features, n_components, time() - t0))
    if hasattr(rp, 'components_'):
        n_bytes = rp.components_.data.nbytes
        n_bytes += rp.components_.indices.nbytes
        print("Random matrix with size: %0.3fMB" % (n_bytes / 1e6))

    projected_dists = euclidean_distances(
        projected_data, squared=True).ravel()[nonzero]

    plt.figure()
    min_dist = min(projected_dists.min(), dists.min())
    max_dist = max(projected_dists.max(), dists.max())
    plt.hexbin(dists, projected_dists, gridsize=100, cmap=plt.cm.PuBu,
               extent=[min_dist, max_dist, min_dist, max_dist])
    plt.xlabel("Pairwise squared distances in original space")
    plt.ylabel("Pairwise squared distances in projected space")
    plt.title("Pairwise distances distribution for n_components=%d" %
              n_components)
    cb = plt.colorbar()
    cb.set_label('Sample pairs counts')

    rates = projected_dists / dists
    print("Mean distances rate: %0.2f (%0.2f)"
          % (np.mean(rates), np.std(rates)))

    plt.figure()
    plt.hist(rates, bins=50, range=(0., 2.), edgecolor='k', **density_param)
    plt.xlabel("Squared distances rate: projected / original")
    plt.ylabel("Distribution of samples pairs")
    plt.title("Histogram of pairwise distance rates for n_components=%d" %
              n_components)

    # TODO: compute the expected value of eps and add them to the previous plot
    # as vertical lines / region

plt.show()

• 
• 
• 
• 
• 
• 

Out:

Embedding 500 samples with dim 130107 using various random projections
Projected 500 samples from 130107 to 300 in 0.306s
Random matrix with size: 1.295MB
Mean distances rate: 1.04 (0.19)
Projected 500 samples from 130107 to 1000 in 2.159s
Random matrix with size: 4.332MB
Mean distances rate: 1.05 (0.10)
Projected 500 samples from 130107 to 10000 in 12.510s
Random matrix with size: 43.251MB
Mean distances rate: 1.01 (0.03)

Podemos ver que para valores bajos de n_components la distribución es amplia con muchos pares distorsionados y una distribución sesgada (debido al límite estricto de la relación cero a la izquierda ya que las distancias son siempre positivas) mientras que para valores mayores que n_components la distorsión está controlada y las distancias están bien conservadas por la proyección aleatoria.

Observaciones

Según el lema JL, proyectar 500 muestras sin demasiada distorsión requerirá al menos varias miles de dimensiones, independientemente del número de características del conjunto de datos original.

Por lo tanto, utilizar proyecciones aleatorias en el conjunto de datos de los dígitos, que sólo tiene 64 características en el espacio de entrada, no tiene sentido: no permite reducir la dimensionalidad en este caso.

Por otro lado, en los veinte grupos de noticias la dimensionalidad puede reducirse de 56436 a 10000 preservando razonablemente las distancias entre pares.