sklearn.random_projection.johnson_lindenstrauss_min_dim¶
- sklearn.random_projection.johnson_lindenstrauss_min_dim()¶
Encuentra un número “seguro” de componentes para proyectar aleatoriamente.
La distorsión introducida por una proyección aleatoria
psólo cambia la distancia entre dos puntos por un factor (1 +- eps) en un espacio euclidiano con buena probabilidad. La proyecciónpes una inserción(embedding) eps definida por:(1 - eps) ||u - v||^2 < ||p(u) - p(v)||^2 < (1 + eps) ||u - v||^2
Donde u y v son cualquier fila tomada de un conjunto de datos de forma (n_samples, n_features), eps está en [0, 1] y p es una proyección por una matriz gaussiana aleatoria N(0, 1) de forma (n_components, n_features) (o una matriz de Achlioptas dispersa).
El número mínimo de componentes para garantizar la inserción eps viene dado por:
n_components >= 4 log(n_samples) / (eps^2 / 2 - eps^3 / 3)
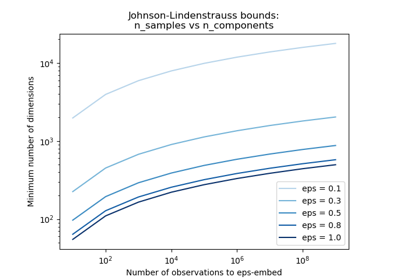
Ten en cuenta que el número de dimensiones es independiente del número original de características, pero en cambio depende del tamaño del conjunto de datos: cuanto más grande es el conjunto de datos, mayor es la dimensionalidad mínima de una inserción eps.
Más información en el Manual de usuario.
- Parámetros
- n_samplesint o array-like de int
Número de muestras que debe ser un entero mayor que 0. Si se da un arreglo, calculará un número seguro de componentes en forma de arreglo.
- epsflotante o ndarray de forma (n_components,), dtype=float, default=0.1
Tasa de distorsión máxima en el rango (0,1 ) definida por el lema de Johnson-Lindenstrauss. Si se da un arreglo, calculará un número seguro de componentes en forma de arreglo.
- Devuelve
- n_componentsint o ndarray de int
El número mínimo de componentes para garantizar con buena probabilidad una inserción eps con n_samples.
Referencias
- 1
https://en.wikipedia.org/wiki/Johnson%E2%80%93Lindenstrauss_lemma
- 2
Sanjoy Dasgupta y Anupam Gupta, 1999, «An elementary proof of the Johnson-Lindenstrauss Lemma.» http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.45.3654
Ejemplos
>>> johnson_lindenstrauss_min_dim(1e6, eps=0.5) 663
>>> johnson_lindenstrauss_min_dim(1e6, eps=[0.5, 0.1, 0.01]) array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim([1e4, 1e5, 1e6], eps=0.1) array([ 7894, 9868, 11841])