3.1. Validación cruzada: evaluación del rendimiento del estimador

Aprender los parámetros de una función de predicción y probarla sobre los mismos datos es un error metodológico: un modelo que se limitase a repetir las etiquetas de las muestras que acaba de ver tendría una puntuación perfecta, pero no lograría predecir nada útil sobre datos aún no vistos. Esta situación se llama sobreajuste. Para evitarla, es práctica común cuando se realiza un experimento de aprendizaje automático (supervisado), el mantener una parte de los datos disponibles como un conjunto de prueba ``X_test, y_test`. Ten en cuenta que la palabra «experimento» no pretende denotar un uso académico únicamente, ya que incluso en entornos comerciales el aprendizaje automático suele comenzar de forma experimental. Este es un diagrama de flujo del proceso de trabajo típico de validación cruzada en el entrenamiento de modelos. Los mejores parámetros pueden determinarse mediante las técnicas de búsqueda en cuadrícula.

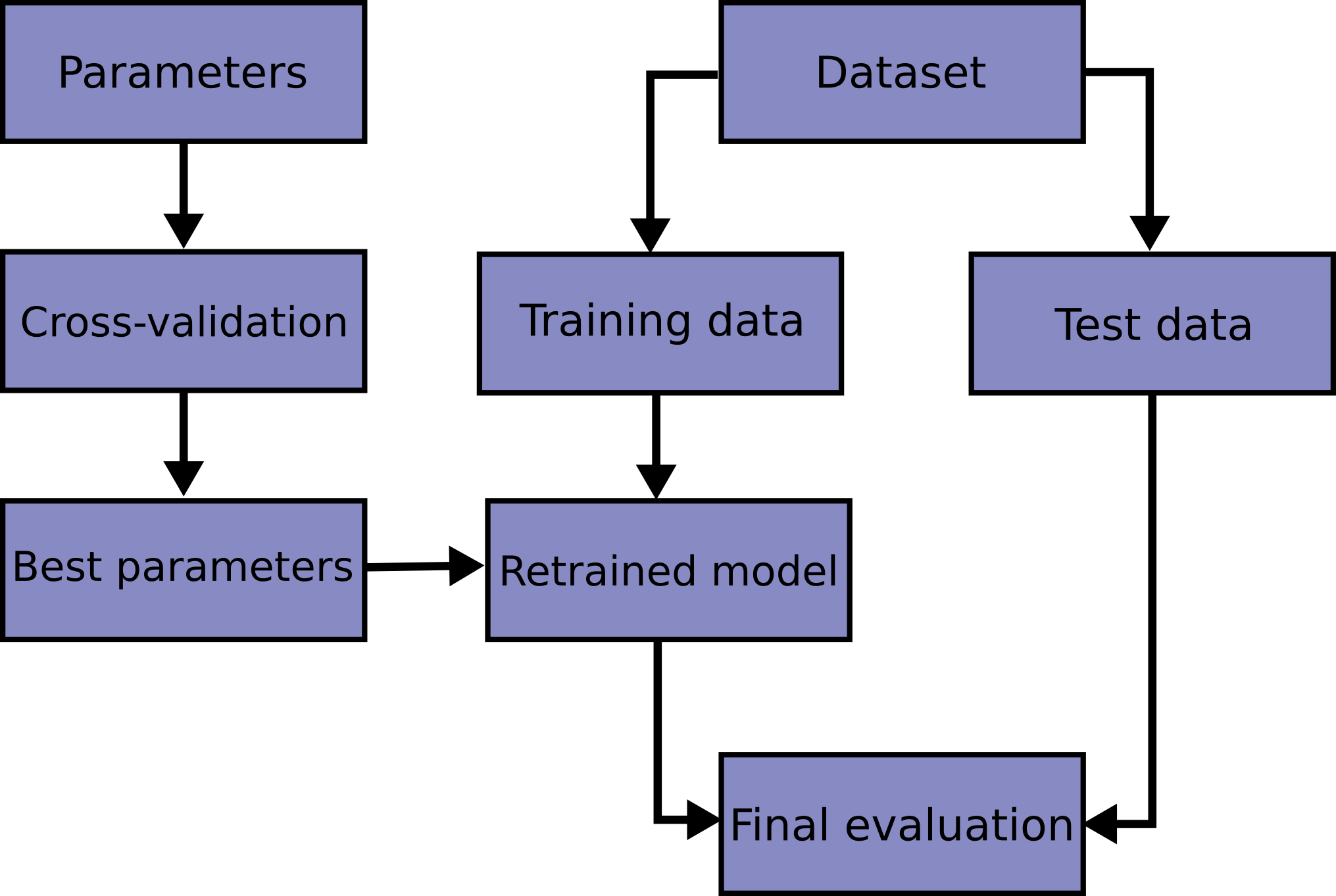
En scikit-learn una división aleatoria en conjuntos de entrenamiento y prueba puede ser rápidamente calculada con la función de ayuda train_test_split. Carguemos el conjunto de datos del iris para ajustar una máquina de vectores de soporte lineal en él:

>>> import numpy as np
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import datasets
>>> from sklearn import svm

>>> X, y = datasets.load_iris(return_X_y=True)
>>> X.shape, y.shape
((150, 4), (150,))

Ahora podemos hacer un muestreo rápido de un conjunto de entrenamiento y reservar el 40% de los datos para probar (evaluar) nuestro clasificador:

>>> X_train, X_test, y_train, y_test = train_test_split(
...     X, y, test_size=0.4, random_state=0)

>>> X_train.shape, y_train.shape
((90, 4), (90,))
>>> X_test.shape, y_test.shape
((60, 4), (60,))

>>> clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.96...

Cuando se evalúan diferentes ajustes («hiperparámetros») para los estimadores, como el ajuste C que debe establecerse manualmente para una SVM, sigue existiendo el riesgo de sobreajuste en el conjunto de prueba porque los parámetros pueden ajustarse hasta que el estimador tenga un rendimiento óptimo. De este modo, el conocimiento sobre el conjunto de pruebas puede «filtrarse» en el modelo y las métricas de evaluación ya no reportan el rendimiento de la generalización. Para resolver este problema, otra parte del conjunto de datos puede mantenerse como el llamado «conjunto de validación»: el entrenamiento se lleva a cabo en el conjunto de entrenamiento, tras lo cual la evaluación se realiza en el conjunto de validación, y cuando el experimento parece ser exitoso, la evaluación final puede realizarse en el conjunto de prueba.

Sin embargo, al dividir los datos disponibles en tres conjuntos, reducimos drásticamente el número de muestras que pueden utilizarse para el aprendizaje del modelo, y los resultados pueden depender de una determinada elección aleatoria del par de conjuntos (de entrenamiento, de validación).

Una solución a este problema es un procedimiento llamado validación cruzada (VC para abreviar). El conjunto de pruebas debe seguir siendo utilizado para la evaluación final, pero el conjunto de validación ya no es necesario cuando se realiza la VC. En el enfoque básico, llamado k-parte VC, el conjunto de entrenamiento se divide en k conjuntos más pequeños (más adelante se describen otros enfoques, pero en general siguen los mismos principios). Se sigue el siguiente procedimiento para cada uno de las k «partes»:

• Se entrena un modelo utilizando \(k-1\) de las partes como datos de entrenamiento;

• el modelo resultante se valida en la parte restante de los datos (es decir, se utiliza como conjunto de pruebas para calcular una medida de rendimiento como la exactitud).

La medida de rendimiento obtenida mediante la validación cruzada de k partes es entonces la media de los valores calculados en el bucle. Este enfoque puede ser costoso desde el punto de vista computacional, pero no desperdicia demasiados datos (como ocurre cuando se fija un conjunto de validación arbitrario), lo que supone una gran ventaja en problemas como la inferencia inversa, donde el número de muestras es muy pequeño.

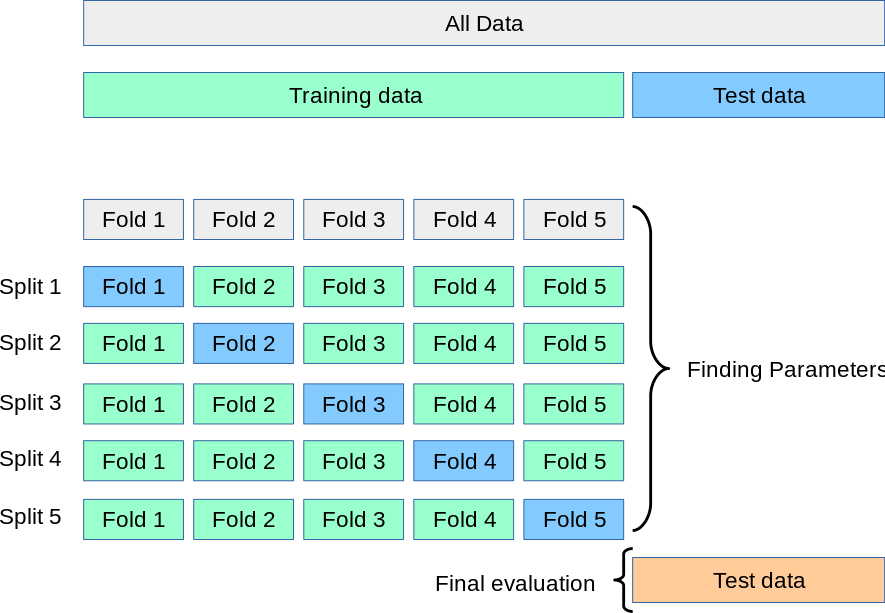
3.1.1. Cálculo de métricas de validación cruzada

La forma más sencilla de utilizar la validación cruzada es llamar a la función de ayuda cross_val_score sobre el estimador y el conjunto de datos.

El siguiente ejemplo muestra cómo estimar la precisión de una máquina de vectores de soporte de núcleo lineal en el conjunto de datos del iris dividiendo los datos, ajustando un modelo y calculando la puntuación 5 veces consecutivas (con diferentes divisiones cada vez):

>>> from sklearn.model_selection import cross_val_score
>>> clf = svm.SVC(kernel='linear', C=1, random_state=42)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores
array([0.96..., 1. , 0.96..., 0.96..., 1. ])

La puntuación media y la desviación estándar vienen dadas por:

>>> print("%0.2f accuracy with a standard deviation of %0.2f" % (scores.mean(), scores.std()))
0.98 accuracy with a standard deviation of 0.02

Por defecto, la puntuación calculada en cada iteración del CV es el método score del estimador. Es posible cambiar esto utilizando el parámetro de puntuación:

>>> from sklearn import metrics
>>> scores = cross_val_score(
...     clf, X, y, cv=5, scoring='f1_macro')
>>> scores
array([0.96..., 1.  ..., 0.96..., 0.96..., 1.        ])

Observa el El parámetro scoring: definir las reglas de evaluación del modelo para más detalles. En el caso del conjunto de datos Iris, las muestras están equilibradas entre las clases objetivo, por lo que la precisión y la puntuación F1 son casi iguales.

Cuando el argumento cv es un entero, cross_val_score utiliza por defecto las estrategias KFold o StratifiedKFold, usándose esta última si el estimador deriva de ClassifierMixin.

También es posible utilizar otras estrategias de validación cruzada pasando un iterador de validación cruzada en su lugar, por ejemplo:

>>> from sklearn.model_selection import ShuffleSplit
>>> n_samples = X.shape[0]
>>> cv = ShuffleSplit(n_splits=5, test_size=0.3, random_state=0)
>>> cross_val_score(clf, X, y, cv=cv)
array([0.977..., 0.977..., 1.  ..., 0.955..., 1.        ])

Otra opción es utilizar un iterable que produzca divisiones (entrenamiento, prueba) como matrices de índices, por ejemplo:

>>> def custom_cv_2folds(X):
...     n = X.shape[0]
...     i = 1
...     while i <= 2:
...         idx = np.arange(n * (i - 1) / 2, n * i / 2, dtype=int)
...         yield idx, idx
...         i += 1
...
>>> custom_cv = custom_cv_2folds(X)
>>> cross_val_score(clf, X, y, cv=custom_cv)
array([1.        , 0.973...])

Transformación de datos con datos retenidos

Al igual que es importante probar un predictor en los datos retenidos del entrenamiento, el preprocesamiento (como la estandarización, la selección de características, etc.) y las transformaciones de datos similares transformaciones de datos deberían aprenderse de un conjunto de entrenamiento y aplicarse a los datos retenidos para la predicción:

>>> from sklearn import preprocessing
>>> X_train, X_test, y_train, y_test = train_test_split(
...     X, y, test_size=0.4, random_state=0)
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> X_train_transformed = scaler.transform(X_train)
>>> clf = svm.SVC(C=1).fit(X_train_transformed, y_train)
>>> X_test_transformed = scaler.transform(X_test)
>>> clf.score(X_test_transformed, y_test)
0.9333...

Un Pipeline facilita la composición de los estimadores, proporcionando este comportamiento bajo validación cruzada:

>>> from sklearn.pipeline import make_pipeline
>>> clf = make_pipeline(preprocessing.StandardScaler(), svm.SVC(C=1))
>>> cross_val_score(clf, X, y, cv=cv)
array([0.977..., 0.933..., 0.955..., 0.933..., 0.977...])

Véase Pipelines y estimadores compuestos.

3.1.1.1. La función cross_validate y la evaluación de métricas múltiples

La función cross_validate difiere de cross_val_score en dos aspectos:

• Permite especificar múltiples métricas para su evaluación.

• Devuelve un diccionario que contiene tiempos de ajuste, tiempos de puntuación (y opcionalmente puntuaciones de entrenamiento así como estimadores ajustados) además de la puntuación de la prueba.

Para la evaluación de una sola métrica, en la que el parámetro de puntuación es una cadena, invocable o None, las claves serán - ['test_score', 'fit_time', 'score_time']

Y para la evaluación de métricas múltiples, el valor de retorno es un diccionario con las siguientes claves - ['test_<scorer1_name>', 'test_<scorer2_name>', 'test_<scorer...>', 'fit_time', 'score_time']

retornar_puntuación_de_entrenamiento se establece por defecto en False para ahorrar tiempo de cálculo. Para evaluar las puntuaciones en el conjunto de entrenamiento también es necesario que se establezca en True.

También puede conservar el estimador ajustado en cada conjunto de entrenamiento estableciendo return_estimator=True.

Las métricas múltiples se pueden especificar como una lista, tupla o conjunto de nombres de puntuadores predefinidos:

>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro', 'recall_macro']
>>> clf = svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores = cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96..., 1.  ..., 0.96..., 0.96..., 1.        ])

O como un diccionario que asigna el nombre del calificador a una función de calificación predefinida o personalizada:

>>> from sklearn.metrics import make_scorer
>>> scoring = {'prec_macro': 'precision_macro',
...            'rec_macro': make_scorer(recall_score, average='macro')}
>>> scores = cross_validate(clf, X, y, scoring=scoring,
...                         cv=5, return_train_score=True)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_prec_macro', 'test_rec_macro',
 'train_prec_macro', 'train_rec_macro']
>>> scores['train_rec_macro']
array([0.97..., 0.97..., 0.99..., 0.98..., 0.98...])

Este es un ejemplo de validación_cruzada utilizando una sola métrica:

>>> scores = cross_validate(clf, X, y,
...                         scoring='precision_macro', cv=5,
...                         return_estimator=True)
>>> sorted(scores.keys())
['estimator', 'fit_time', 'score_time', 'test_score']

3.1.1.2. Obtención de predicciones por validación cruzada

La función cross_val_predict tiene una interfaz similar a la de cross_val_score, pero devuelve, para cada elemento de la entrada, la predicción que se obtuvo para ese elemento cuando estaba en el conjunto de prueba. Sólo pueden utilizarse las estrategias de validación cruzada que asignan todos los elementos a un conjunto de prueba exactamente una vez (en caso contrario, se produce una excepción).

Advertencia

Nota sobre el uso inadecuado de cross_val_predict

El resultado de cross_val_predict puede ser diferente de los obtenidos usando cross_val_score ya que los elementos se agrupan de diferentes maneras. La función cross_val_score toma un promedio sobre los pliegues de validación, mientras que cross_val_predict simplemente devuelve las etiquetas (o probabilidades) de varios modelos distintos no listados. Así, cross_val_predict no es una medida apropiada de error de generalización.

La función cross_val_predict es apropiada para:

• Visualización de las predicciones obtenidas a partir de diferentes modelos.

• Mezcla de modelos: Cuando las predicciones de un estimador supervisado se utilizan para entrenar a otro estimador en métodos de conjunto.

Los iteradores de validación cruzada disponibles se presentan en la siguiente sección.

Ejemplos

• Característica operativa del receptor (Receiver Operating Characteristic, ROC) con validación cruzada,

• Eliminación recursiva de características con validación cruzada,

• Estimación de parámetros utilizando la búsqueda en cuadrícula con validación cruzada,

• Ejemplo de pipeline para la extracción y evaluación de características de texto,

• Graficando predicciones con validación cruzada,

• Validación cruzada anidada y no anidada.

3.1.2. Iteradores de validación cruzada

En las siguientes secciones se enumeran las utilidades para generar índices que pueden utilizarse para generar divisiones de conjuntos de datos según diferentes estrategias de validación cruzada.

3.1.2.1. Iteradores de validación cruzada para datos i.i.d

Asumir que unos datos son independientes e idénticamente distribuidos (i.i.d.) es hacer la suposición de que todas las muestras provienen del mismo proceso generativo y que se supone que el proceso generativo no tiene memoria de las muestras generadas anteriormente.

En estos casos se pueden utilizar los siguientes validadores cruzados.

Nota

Aunque los datos i.i.d. son una suposición común en la teoría del aprendizaje automático, rara vez ésto se cumple en la práctica. Si se sabe que las muestras se han generado utilizando un proceso dependiente del tiempo, es más seguro utilizar un esquema de validación cruzada que tenga en cuenta las series temporales . Del mismo modo, si sabemos que el proceso generativo tiene una estructura de grupo (muestras recogidas de diferentes sujetos, experimentos, dispositivos de medición), es más seguro utilizar validación cruzada en función del grupo.

3.1.2.1.1. K-fold

KFold divide todas las muestras en \(k\) grupos de muestras, llamados partes (si \(k = n\), esto equivale a la estrategia Leave One Out), de igual tamaño (si es posible). La función de predicción se aprende utilizando \(k - 1\) partes, y la parte que se deja fuera se utiliza para la prueba.

Ejemplo de validación cruzada de 2 partes en un conjunto de datos con 4 muestras:

>>> import numpy as np
>>> from sklearn.model_selection import KFold

>>> X = ["a", "b", "c", "d"]
>>> kf = KFold(n_splits=2)
>>> for train, test in kf.split(X):
...     print("%s %s" % (train, test))
[2 3] [0 1]
[0 1] [2 3]

Aquí hay una visualización del comportamiento de la validación cruzada. Ten en cuenta que KFold no se ve afectado por las clases o grupos.

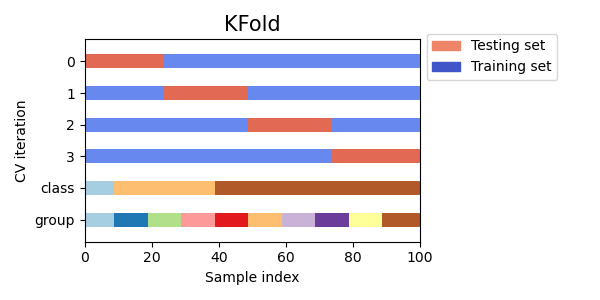
Cada parte está constituida por dos matrices: la primera está relacionada con el conjunto de entrenamiento, y la segunda con el conjunto de prueba. Así, se pueden crear los conjuntos de entrenamiento/prueba utilizando la indexación de numpy:

>>> X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
>>> y = np.array([0, 1, 0, 1])
>>> X_train, X_test, y_train, y_test = X[train], X[test], y[train], y[test]

3.1.2.1.2. K-Fold repetido

RepeatedKFold repite K-Fold n veces. Se puede utilizar cuando se requiere ejecutar KFold n veces, produciendo diferentes divisiones en cada repetición.

Ejemplo de K-Fold repetido 2 veces:

>>> import numpy as np
>>> from sklearn.model_selection import RepeatedKFold
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> random_state = 12883823
>>> rkf = RepeatedKFold(n_splits=2, n_repeats=2, random_state=random_state)
>>> for train, test in rkf.split(X):
...     print("%s %s" % (train, test))
...
[2 3] [0 1]
[0 1] [2 3]
[0 2] [1 3]
[1 3] [0 2]

Del mismo modo, RepeatedStratifiedKFold repite el K-Fold estratificado n veces con una aleatorización diferente en cada repetición.

3.1.2.1.3. Leave One Out (LOO)

LeaveOneOut (o LOO) es una simple validación cruzada. Cada conjunto de aprendizaje se crea tomando todas las muestras excepto una, siendo el conjunto de prueba la muestra que se deja fuera. Así, para \(n\) muestras, tenemos \(n\) conjuntos de entrenamiento diferentes y \(n\) conjuntos de prueba diferentes. Este procedimiento de validación cruzada no desperdicia muchos datos, ya que sólo se elimina una muestra del conjunto de entrenamiento:

>>> from sklearn.model_selection import LeaveOneOut

>>> X = [1, 2, 3, 4]
>>> loo = LeaveOneOut()
>>> for train, test in loo.split(X):
...     print("%s %s" % (train, test))
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]

Los usuarios potenciales de LOO para la selección de modelos deben sopesar algunas advertencias conocidas. Cuando se compara con la validación cruzada \(k\), se construyen modelos \(n\) a partir de muestras \(n\) en lugar de modelos \(k\), donde \(n > k\). Además, cada uno se entrena con muestras \(n - 1\) en lugar de \((k-1) n / k\). En ambos casos, asumiendo que \(k\) no es demasiado grande y que \(k < n\), LOO es más costoso computacionalmente que la validación cruzada de \(k\).

En términos de precisión, la LOO suele dar lugar a una alta varianza como estimador del error de la prueba. Intuitivamente, dado que \(n - 1\) de las muestras \(n\) se utilizan para construir cada modelo, los modelos construidos a partir de partes son prácticamente idénticos entre sí y al modelo construido a partir del conjunto de entrenamiento completo.

Sin embargo, si la curva de aprendizaje es pronunciada para el volumen de entrenamiento en cuestión, la validación cruzada de 5 o 10 partes puede sobreestimar el error de generalización.

Como regla general, la mayoría de los autores, y la evidencia empírica, sugieren que la validación cruzada de 5 o 10 partes debería preferirse a la LOO.

Referencias:

• http://www.faqs.org/faqs/ai-faq/neural-nets/part3/section-12.html;

• T. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning, Springer 2009

• L. Breiman, P. Spector Submodel selection and evaluation in regression: The X-random case, International Statistical Review 1992;

• R. Kohavi, A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection, Intl. Jnt. Conf. AI

• R. Bharat Rao, G. Fung, R. Rosales, On the Dangers of Cross-Validation. An Experimental Evaluation, SIAM 2008;

• G. James, D. Witten, T. Hastie, R Tibshirani, An Introduction to Statistical Learning, Springer 2013.

3.1.2.1.4. Leave P Out (LPO)

LeavePOut es muy similar a LeaveOneOut ya que crea todos los posibles conjuntos de entrenamiento/prueba eliminando las muestras \(p\) del conjunto completo. Para las muestras de \(n\), esto produce pares de entrenamiento-prueba de \({n \choose p}\). A diferencia de LeaveOneOut y KFold, los conjuntos de prueba se superponen para \(p > 1\).

Ejemplo de Leave-2-Out en un conjunto de datos con 4 muestras:

>>> from sklearn.model_selection import LeavePOut

>>> X = np.ones(4)
>>> lpo = LeavePOut(p=2)
>>> for train, test in lpo.split(X):
...     print("%s %s" % (train, test))
[2 3] [0 1]
[1 3] [0 2]
[1 2] [0 3]
[0 3] [1 2]
[0 2] [1 3]
[0 1] [2 3]

3.1.2.1.5. Validación cruzada de permutaciones aleatorias, también conocida como Mezcla y División

El iterador ShuffleSplit generará un número definido por el usuario de divisiones independientes del conjunto de datos de entrenamiento/prueba. Las muestras se barajan primero y luego se dividen en un par de conjuntos de entrenamiento y prueba.

Es posible controlar la aleatoriedad para la reproducibilidad de los resultados sembrando explícitamente el generador de números pseudoaleatorios random_state.

Este es un ejemplo de uso:

>>> from sklearn.model_selection import ShuffleSplit
>>> X = np.arange(10)
>>> ss = ShuffleSplit(n_splits=5, test_size=0.25, random_state=0)
>>> for train_index, test_index in ss.split(X):
...     print("%s %s" % (train_index, test_index))
[9 1 6 7 3 0 5] [2 8 4]
[2 9 8 0 6 7 4] [3 5 1]
[4 5 1 0 6 9 7] [2 3 8]
[2 7 5 8 0 3 4] [6 1 9]
[4 1 0 6 8 9 3] [5 2 7]

Aquí hay una visualización del comportamiento de la validación cruzada. Tenga en cuenta que ShuffleSplit no se ve afectado por las clases o grupos.

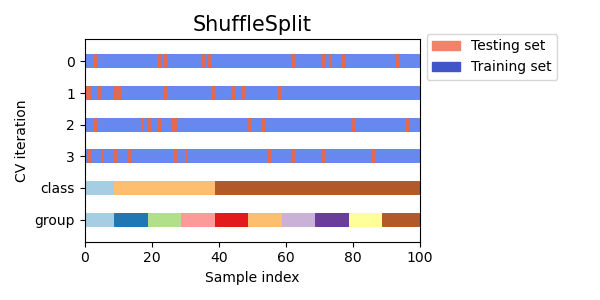
Por tanto, ShuffleSplit es una buena alternativa a la validación cruzada KFold que permite un control más fino del número de iteraciones y de la proporción de muestras en cada lado de la división entrenamiento/prueba.

3.1.2.2. Iteradores de validación cruzada con estratificación basada en las etiquetas de clase.

Algunos problemas de clasificación pueden presentar un gran desequilibrio en la distribución de las clases objetivo: por ejemplo, puede haber varias veces más muestras negativas que positivas. En estos casos se recomienda utilizar el muestreo estratificado como se implementa en StratifiedKFold y StratifiedShuffleSplit para asegurar que las frecuencias relativas de las clases se conserven aproximadamente en cada parte de entrenamiento y validación.

3.1.2.2.1. K-fold estratificado

StratifiedKFold es una variación de k-fold que devuelve partes estratificadas: cada conjunto contiene aproximadamente el mismo porcentaje de muestras de cada clase objetivo que el conjunto completo.

Este es un ejemplo de validación cruzada estratificada de 3 partes en un conjunto de datos con 50 muestras de dos clases no equilibradas. Se presenta el número de muestras de cada clase y se compara con KFold.

>>> from sklearn.model_selection import StratifiedKFold, KFold
>>> import numpy as np
>>> X, y = np.ones((50, 1)), np.hstack(([0] * 45, [1] * 5))
>>> skf = StratifiedKFold(n_splits=3)
>>> for train, test in skf.split(X, y):
...     print('train -  {}   |   test -  {}'.format(
...         np.bincount(y[train]), np.bincount(y[test])))
train -  [30  3]   |   test -  [15  2]
train -  [30  3]   |   test -  [15  2]
train -  [30  4]   |   test -  [15  1]
>>> kf = KFold(n_splits=3)
>>> for train, test in kf.split(X, y):
...     print('train -  {}   |   test -  {}'.format(
...         np.bincount(y[train]), np.bincount(y[test])))
train -  [28  5]   |   test -  [17]
train -  [28  5]   |   test -  [17]
train -  [34]   |   test -  [11  5]

Podemos ver que StratifiedKFold preserva los ratios de clase (aproximadamente 1 / 10) tanto en el conjunto de datos de entrenamiento como en el de prueba.

Aquí hay una visualización del comportamiento de la validación cruzada.

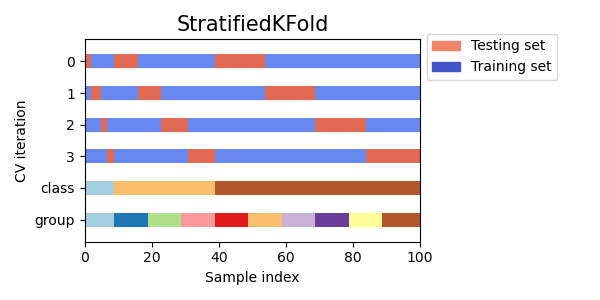
RepeatedStratifiedKFold se puede utilizar para repetir el K-Fold Estratificado n veces con diferente aleatorización en cada repetición.

3.1.2.2.2. División aleatoria estratificada

StratifiedShuffleSplit es una variación de Mezcla y División, que devuelve divisiones estratificadas, es decir que crea divisiones conservando el mismo porcentaje para cada clase objetivo que en el conjunto completo.

Aquí hay una visualización del comportamiento de la validación cruzada.

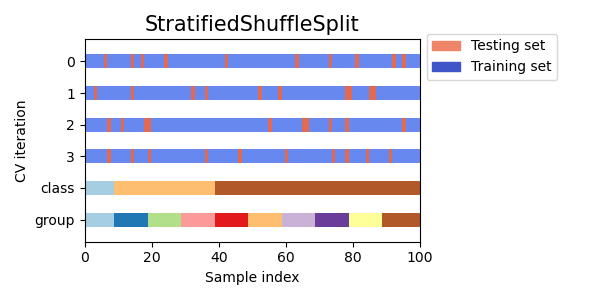
3.1.2.3. Iteradores de validación cruzada para datos agrupados.

La suposición i.i.d. se rompe si el proceso generativo subyacente produce grupos de muestras dependientes.

Tal agrupación de datos es específica del dominio. Un ejemplo sería cuando hay datos médicos recogidos de múltiples pacientes, con múltiples muestras tomadas de cada paciente. Y es probable que esos datos sean dependientes del grupo individual. En nuestro ejemplo, el identificador del paciente de cada muestra será su identificador de grupo.

En este caso, nos gustaría saber si un modelo entrenado en un determinado conjunto de grupos generaliza bien a los grupos no vistos. Para medirlo, tenemos que asegurarnos de que todas las muestras en esa parte de la validación proceden de grupos que no están representados en absoluto en la parte de entrenamiento emparejado.

Para ello, se pueden utilizar los siguientes divisores de validación cruzada. El identificador de agrupación de las muestras se especifica mediante el parámetro groups.

3.1.2.3.1. K-fold de grupos

GroupKFold es una variación de k-fold que garantiza que el mismo grupo no esté representado en los conjuntos de prueba y de entrenamiento. Por ejemplo, si los datos se obtienen de diferentes sujetos con varias muestras por sujeto y si el modelo es lo suficientemente flexible como para aprender de características muy específicas de la persona, podría fallar al generalizar para nuevos sujetos. GroupKFold permite detectar este tipo de situaciones de sobreajuste.

Imagina que tienes tres sujetos, cada uno con un número asociado del 1 al 3:

>>> from sklearn.model_selection import GroupKFold

>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 8.8, 9, 10]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "d", "d", "d"]
>>> groups = [1, 1, 1, 2, 2, 2, 3, 3, 3, 3]

>>> gkf = GroupKFold(n_splits=3)
>>> for train, test in gkf.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[0 1 2 3 4 5] [6 7 8 9]
[0 1 2 6 7 8 9] [3 4 5]
[3 4 5 6 7 8 9] [0 1 2]

Cada sujeto está en un pliegue de prueba diferente, y el mismo sujeto nunca está tanto en la prueba como en el entrenamiento. Observa que las partes no tienen exactamente el mismo tamaño debido al desequilibrio de los datos.

Aquí hay una visualización del comportamiento de la validación cruzada.

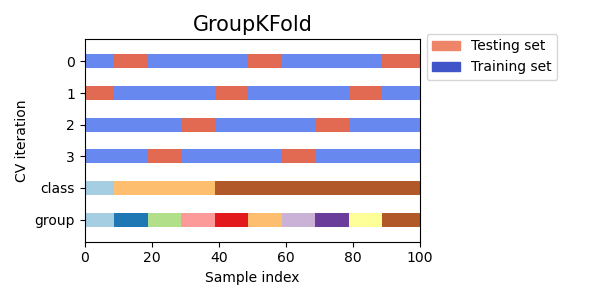
3.1.2.3.2. Dejar un grupo afuera (Leave One Group Out)

LeaveOneGroupOut es un esquema de validación cruzada que mantiene las muestras según una matriz de grupos enteros proporcionada por terceros. Esta información de grupo puede utilizarse para codificar partes de validación cruzada predefinidas y específicas del dominio.

De este modo, cada conjunto de entrenamiento está constituido por todas las muestras excepto las relacionadas con un grupo específico.

Por ejemplo, en los casos de experimentos múltiples, se puede utilizar LeaveOneGroupOut para crear una validación cruzada basada en los diferentes experimentos: creamos un conjunto de entrenamiento utilizando las muestras de todos los experimentos excepto uno:

>>> from sklearn.model_selection import LeaveOneGroupOut

>>> X = [1, 5, 10, 50, 60, 70, 80]
>>> y = [0, 1, 1, 2, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3, 3]
>>> logo = LeaveOneGroupOut()
>>> for train, test in logo.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[2 3 4 5 6] [0 1]
[0 1 4 5 6] [2 3]
[0 1 2 3] [4 5 6]

Otra aplicación común es utilizar información temporal: por ejemplo, los grupos podrían ser el año de recogida de las muestras y así permitir la validación cruzada contra divisiones basadas en el tiempo.

3.1.2.3.3. Dejar fuera los grupos P

LeavePGroupsOut es similar a LeaveOneGroupOut, pero elimina las muestras relacionadas con los grupos de \(P\) para cada conjunto de entrenamiento/prueba.

Ejemplo de Dejar-2-Grupos Afuera:

>>> from sklearn.model_selection import LeavePGroupsOut

>>> X = np.arange(6)
>>> y = [1, 1, 1, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3]
>>> lpgo = LeavePGroupsOut(n_groups=2)
>>> for train, test in lpgo.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[4 5] [0 1 2 3]
[2 3] [0 1 4 5]
[0 1] [2 3 4 5]

3.1.2.3.4. Dividir grupos de forma aleatoria

El iterador GroupShuffleSplit se comporta como una combinación de ShuffleSplit y LeavePGroupsOut, y genera una secuencia de particiones aleatorias en las que se mantiene un subconjunto de grupos para cada partición.

Este es un ejemplo de uso:

>>> from sklearn.model_selection import GroupShuffleSplit

>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "a"]
>>> groups = [1, 1, 2, 2, 3, 3, 4, 4]
>>> gss = GroupShuffleSplit(n_splits=4, test_size=0.5, random_state=0)
>>> for train, test in gss.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
...
[0 1 2 3] [4 5 6 7]
[2 3 6 7] [0 1 4 5]
[2 3 4 5] [0 1 6 7]
[4 5 6 7] [0 1 2 3]

Aquí hay una visualización del comportamiento de la validación cruzada.

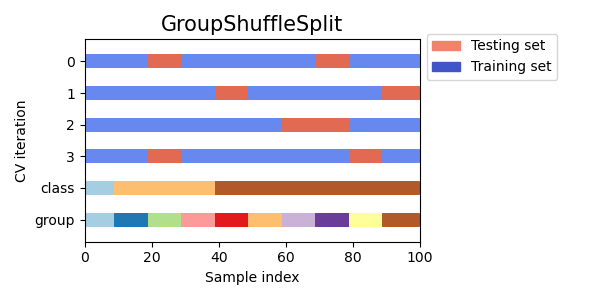
Esta clase es útil cuando se desea el comportamiento de LeavePGroupsOut, pero el número de grupos es lo suficientemente grande como para que generar todas las posibles particiones con grupos retenidos de \(P\) sea prohibitivamente costoso. En este caso, GroupShuffleSplit proporciona una muestra aleatoria (con reemplazo) de las particiones de entrenamiento/prueba generadas por LeavePGroupsOut.

3.1.2.4. Divisiones predefinidas/ Conjuntos de validación

Para algunos conjuntos de datos, ya existe una división predefinida de los datos en pliegues (fold) de entrenamiento y validación o en varios pliegues de validación cruzada. Utilizando PredefinedSplit es posible utilizar estos pliegues, por ejemplo, cuando se buscan hiperparámetros.

Por ejemplo, cuando se utiliza un conjunto de validación, establezca el test_fold a 0 para todas las muestras que forman parte del conjunto de validación, y a -1 para todas las demás muestras.

3.1.2.5. Uso de los iteradores de validación cruzada para dividir el entrenamiento y la prueba

Las anteriores funciones de validación cruzada de grupo también pueden ser útiles para dividir un conjunto de datos en subconjuntos de entrenamiento y prueba. Ten en cuenta que la función de conveniencia train_test_split es un envoltorio de ShuffleSplit y, por tanto, sólo permite la división estratificada (utilizando las etiquetas de clase) y no puede tener en cuenta los grupos.

Para realizar la división de entrenamiento y prueba, utiliza los índices de los subconjuntos de entrenamiento y prueba producidos por la salida del generador mediante el método split() del divisor de validación cruzada. Por ejemplo:

>>> import numpy as np
>>> from sklearn.model_selection import GroupShuffleSplit

>>> X = np.array([0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001])
>>> y = np.array(["a", "b", "b", "b", "c", "c", "c", "a"])
>>> groups = np.array([1, 1, 2, 2, 3, 3, 4, 4])
>>> train_indx, test_indx = next(
...     GroupShuffleSplit(random_state=7).split(X, y, groups)
... )
>>> X_train, X_test, y_train, y_test = \
...     X[train_indx], X[test_indx], y[train_indx], y[test_indx]
>>> X_train.shape, X_test.shape
((6,), (2,))
>>> np.unique(groups[train_indx]), np.unique(groups[test_indx])
(array([1, 2, 4]), array([3]))

3.1.2.6. Validación cruzada de datos de series de tiempo

Los datos de las series de tiempo se caracterizan por la correlación entre observaciones cercanas en el tiempo (autocorrelación). Sin embargo, las técnicas clásicas de validación cruzada, como KFold y ShuffleSplit, suponen que las muestras son independientes y están idénticamente distribuidas, y darían lugar a una correlación poco razonable entre las instancias de entrenamiento y las de prueba (lo que daría lugar a malas estimaciones del error de generalización) en los datos de series de tiempo. Por lo tanto, es muy importante evaluar nuestro modelo para datos de series de tiempo en las observaciones «futuras» menos parecidas a las que se utilizan para entrenar el modelo. Para conseguirlo, una solución es la que proporciona TimeSeriesSplit.

3.1.2.6.1. División de series de tiempo

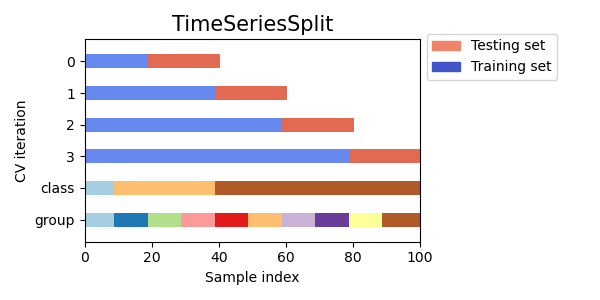
TimeSeriesSplit es una variación de k-fold que devuelve los primeros pliegues de \(k\) como conjunto de entrenamiento y el \((k+1)\) última parte como conjunto de prueba. Tenga en cuenta que, a diferencia de los métodos estándar de validación cruzada, los conjuntos de entrenamiento sucesivos son superconjuntos de los que vienen antes. Además, añade todos los datos sobrantes a la primera partición de entrenamiento, que siempre se utiliza para entrenar el modelo.

Esta clase puede utilizarse para la validación cruzada de muestras de datos de series de tiempo que se observan en intervalos de tiempo fijos.

Ejemplo de validación cruzada de series de tiempo con 3 divisiones en un conjunto de datos con 6 muestras:

>>> from sklearn.model_selection import TimeSeriesSplit

>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> tscv = TimeSeriesSplit(n_splits=3)
>>> print(tscv)
TimeSeriesSplit(gap=0, max_train_size=None, n_splits=3, test_size=None)
>>> for train, test in tscv.split(X):
...     print("%s %s" % (train, test))
[0 1 2] [3]
[0 1 2 3] [4]
[0 1 2 3 4] [5]

Aquí hay una visualización del comportamiento de la validación cruzada.

3.1.3. Nota sobre la mezcla

Si el orden de los datos no es arbitrario (por ejemplo, las muestras con la misma etiqueta de clase son contiguas), revolverlas primero puede ser esencial para obtener un resultado de validación cruzada significativo. Sin embargo, puede ocurrir lo contrario si las muestras no están distribuidas de forma independiente e idéntica. Por ejemplo, si las muestras corresponden a artículos de noticias, y están ordenadas por su hora de publicación, entonces revolver los datos probablemente conducirá a un modelo sobreajustado y a una puntuación de validación inflada: se probará en muestras que son artificialmente similares (cercanas en el tiempo) a las muestras de entrenamiento.

Algunos iteradores de validación cruzada, como KFold, tienen una opción incorporada para revolver los índices de datos antes de dividirlos. Ten en cuenta que:

• Esto consume menos memoria que revolver los datos directamente.

• Por defecto no se revuelve, incluso para la validación cruzada (estratificada) de K pliegues que se realiza especificando cv=algunos_integros a cross_val_score, búsqueda en cuadrícula, etc. Ten en cuenta que train_test_split sigue devolviendo una división aleatoria.

• El parámetro random_state es por defecto None, lo que significa que la forma de mezclar será diferente cada vez que se itere KFold(..., shuffle=True). Sin embargo, GridSearchCV utilizará el mismo proceso de mezclar para cada conjunto de parámetros validados por una única llamada a su método fit.

• Para obtener resultados idénticos para cada división, establezca random_state a un número entero.

Para más detalles sobre cómo controlar la aleatoriedad de los divisores de cv y evitar errores comunes, véase Control de aleatoriedad.

3.1.4. Validación cruzada y selección de modelos

Los iteradores de validación cruzada también pueden utilizarse para realizar directamente la selección del modelo mediante la búsqueda en cuadrícula de los hiperparámetros óptimos del modelo. Este es el tema de la siguiente sección: Ajustar los hiperparámetros de un estimador.

3.1.5. Puntuación de la prueba de permutación

permutation_test_score ofrece otra forma de evaluar el rendimiento de los clasificadores. Proporciona un valor p basado en la permutación, que representa la probabilidad de que un rendimiento observado del clasificador se obtenga por azar. La hipótesis nula en esta prueba es que el clasificador no aprovecha ninguna dependencia estadística entre las características y las etiquetas para hacer predicciones correctas en los datos omitidos. permutation_test_score genera una distribución nula calculando n_permutaciones diferentes de los datos. En cada permutación las etiquetas se revuelven aleatoriamente, eliminando así cualquier dependencia entre las características y las etiquetas. El valor p resultante es la fracción de permutaciones para las que la puntuación media de validación cruzada obtenida por el modelo es mejor que la puntuación de validación cruzada obtenida por el modelo utilizando los datos originales. Para obtener resultados fiables, n_permutaciones debe ser normalmente superior a 100 y cv entre 3-10 partes.

Un valor p bajo demuestra que el conjunto de datos contiene una dependencia real entre las características y las etiquetas y que el clasificador ha sido capaz de utilizarla para obtener buenos resultados. Un valor p alto podría deberse a la falta de dependencia entre las características y las etiquetas (no hay diferencias en los valores de las características entre las clases) o a que el clasificador no fue capaz de utilizar la dependencia en los datos. En este último caso, el uso de un clasificador más adecuado que sea capaz de utilizar la estructura de los datos daría lugar a un valor p bajo.

La validación cruzada proporciona información sobre el grado de generalización de un clasificador, concretamente el rango de errores esperados del clasificador. Sin embargo, un clasificador entrenado en un conjunto de datos de alta dimensión sin estructura puede tener un rendimiento mejor de lo esperado en la validación cruzada, por pura casualidad. Esto puede ocurrir típicamente con conjuntos de datos pequeños con menos de unos cientos de muestras. permutation_test_score proporciona información sobre si el clasificador ha encontrado una estructura de clase real y puede ayudar a evaluar el rendimiento del clasificador.

Es importante señalar que se ha demostrado que esta prueba produce valores p bajos incluso si sólo hay una estructura débil en los datos, porque en los conjuntos de datos permutados correspondientes no hay absolutamente ninguna estructura. Por lo tanto, esta prueba sólo es capaz de mostrar cuándo el modelo supera de forma fiable las conjeturas al azar.

Por último, permutation_test_score se calcula utilizando la fuerza bruta y se ajusta internamente a los modelos (n_permutations + 1) * n_cv. Por lo tanto, sólo es viable con conjuntos de datos pequeños para los que el ajuste de un modelo individual es muy rápido.

Ejemplos

• Evalúa con permutaciones la importancia de una puntuación de clasificación

Referencias:

• Ojala and Garriga. Permutation Tests for Studying Classifier Performance. J. Mach. Learn. Res. 2010.