Evalúa con permutaciones la importancia de una puntuación de clasificación

Este ejemplo demuestra el uso de permutation_test_score para evaluar la importancia de una puntuación cruzada utilizando permutaciones.

# Authors:  Alexandre Gramfort <alexandre.gramfort@inria.fr>
#           Lucy Liu
# License: BSD 3 clause
#
# Dataset
# -------
#
# We will use the :ref:`iris_dataset`, which consists of measurements taken
# from 3 types of irises.

from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target

También generaremos algunos datos de características aleatorias (es decir, 2200 características), no correlacionadas con las etiquetas de clase en el conjunto de datos del iris.

import numpy as np

n_uncorrelated_features = 2200
rng = np.random.RandomState(seed=0)
# Use same number of samples as in iris and 2200 features
X_rand = rng.normal(size=(X.shape[0], n_uncorrelated_features))

Puntuación de la prueba de permutación

A continuación, calculamos el ermutation_test_score usando el conjunto de datos de iris original, que predice fuertemente las etiquetas y las características generadas al azar y las etiquetas de iris, que no deberían tener dependencia entre características y etiquetas. Utilizamos el clasificación SVC y Puntuación de precisión para evaluar el modelo en cada ronda.

permutation_test_score genera una distribución nula calculando la exactitud del clasificador en 1000 permutaciones diferentes del conjunto de datos, donde las características siguen siendo las mismas pero las etiquetas sufren diferentes permutaciones. Esta es la distribución para la hipótesis nula que afirma que no hay dependencia entre las características y las etiquetas. A continuación, se calcula un valor p empírico como el porcentaje de permutaciones en las que la puntuación obtenida es mayor que la obtenida con los datos originales.

from sklearn.svm import SVC
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import permutation_test_score

clf = SVC(kernel='linear', random_state=7)
cv = StratifiedKFold(2, shuffle=True, random_state=0)

score_iris, perm_scores_iris, pvalue_iris = permutation_test_score(
    clf, X, y, scoring="accuracy", cv=cv, n_permutations=1000)

score_rand, perm_scores_rand, pvalue_rand = permutation_test_score(
    clf, X_rand, y, scoring="accuracy", cv=cv, n_permutations=1000)

Datos originales

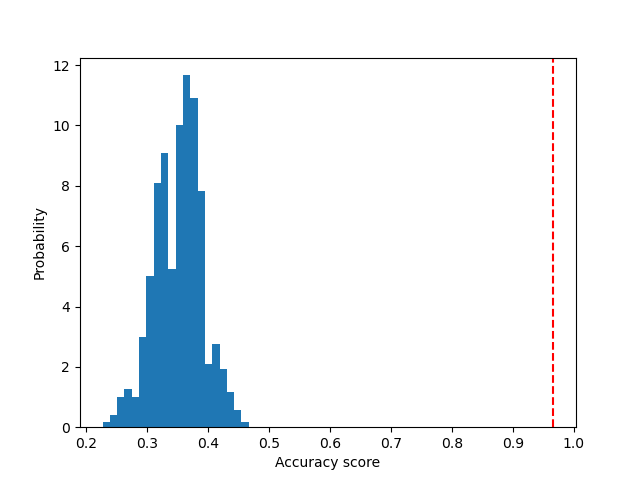
A continuación, trazamos un histograma de las puntuaciones de permutación (la distribución nula). La línea roja indica la puntuación obtenida por el clasificador en los datos originales. La puntuación es mucho mejor que la obtenida con los datos permutados y, por tanto, el valor p es muy bajo. Esto indica que hay una baja verosimilitud de que esta buena puntuación se obtenga sólo por azar. Esto demuestra que el conjunto de datos del iris contiene una dependencia real entre las características y las etiquetas, y que el clasificador fue capaz de utilizarla para obtener buenos resultados.

import matplotlib.pyplot as plt

fig, ax = plt.subplots()

ax.hist(perm_scores_iris, bins=20, density=True)
ax.axvline(score_iris, ls='--', color='r')
score_label = (f"Score on original\ndata: {score_iris:.2f}\n"
               f"(p-value: {pvalue_iris:.3f})")
ax.text(0.7, 260, score_label, fontsize=12)
ax.set_xlabel("Accuracy score")
_ = ax.set_ylabel("Probability")

Datos aleatorios

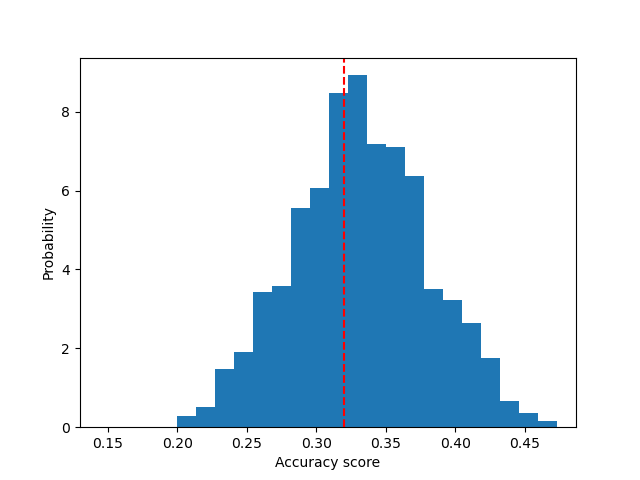
A continuación, trazamos la distribución nula para los datos aleatorios. Las puntuaciones de la permutación son similares a las obtenidas con el conjunto de datos original del iris, ya que la permutación siempre destruye cualquier dependencia de la etiqueta de características presente. Sin embargo, la puntuación obtenida con los datos aleatorios originales es muy baja. El resultado es un gran valor p, lo que confirma que no había dependencia de etiquetas de características en los datos originales.

fig, ax = plt.subplots()

ax.hist(perm_scores_rand, bins=20, density=True)
ax.set_xlim(0.13)
ax.axvline(score_rand, ls='--', color='r')
score_label = (f"Score on original\ndata: {score_rand:.2f}\n"
               f"(p-value: {pvalue_rand:.3f})")
ax.text(0.14, 125, score_label, fontsize=12)
ax.set_xlabel("Accuracy score")
ax.set_ylabel("Probability")
plt.show()

Otra posible razón para obtener un valor p alto es que el clasificador no pudo usar la estructura en los datos. En este caso, el valor p sólo sería bajo para los clasificadores que son capaces de utilizar la dependencia presente. En nuestro caso anterior, donde los datos son aleatorios, todos los clasificadores tendrían un alto valor p, ya que no hay estructura presente en los datos.

Por último, ten en cuenta que esta prueba ha sido mostrada para producir valores de p bajos, incluso si solo hay una estructura débil en los datos 1.

Referencias:

1

Ojala and Garriga. Permutation Tests for Studying Classifier Performance. The Journal of Machine Learning Research (2010) vol. 11