`sklearn.mixture`.BayesianGaussianMixture¶

class sklearn.mixture.BayesianGaussianMixture¶

Estimación variacional Bayesiana de una mezcla Gaussiana.

Esta clase permite inferir una distribución a posteriori aproximada sobre los parámetros de una distribución de mezcla Gaussiana. El número efectivo de componentes puede inferirse a partir de los datos.

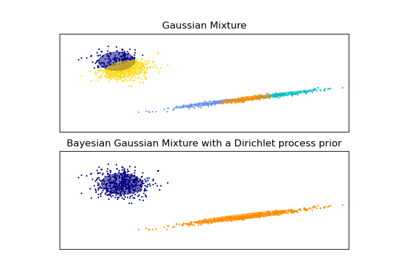
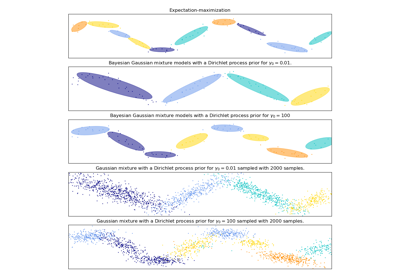
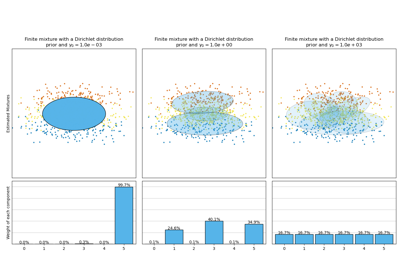
Esta clase implementa dos tipos de a priori para la distribución de las ponderaciones: un modelo de mezcla finita con distribución de Dirichlet y un modelo de mezcla infinita con el Proceso de Dirichlet. En la práctica, el algoritmo de inferencia del Proceso de Dirichlet se aproxima y utiliza una distribución truncada con un número máximo fijo de componentes (denominada representación Stick-breaking, ruptura de palos en español). El número de componentes realmente utilizado depende casi siempre de los datos.

Nuevo en la versión 0.18.

Lee más en el Manual de usuario.

Parámetros

n_componentsint, default=1

El número de componentes de la mezcla. Dependiendo de los datos y del valor del weight_concentration_prior el modelo puede decidir no utilizar todos los componentes estableciendo algunos weights_ de los componentes en valores muy cercanos a cero. Por tanto, el número de componentes efectivos es menor que n_components.

covariance_type{“full”, “tied”, “diag”, “spherical”}, default=”full”

Cadena que describe el tipo de parámetros de covarianza a utilizar. Debe ser uno de los siguientes:

'full' (each component has its own general covariance matrix),
'tied' (all components share the same general covariance matrix),
'diag' (each component has its own diagonal covariance matrix),
'spherical' (each component has its own single variance).

tolfloat, default=1e-3

El umbral de convergencia. Las iteraciones EM se detendrán cuando la ganancia promedio del límite inferior sobre la verosimilitud (de los datos de entrenamiento con respecto al modelo) esté por debajo de este umbral.

reg_covarfloat, default=1e-6

La regularización no negativa añadida a la diagonal de la covarianza. Permite asegurar que las matrices de covarianzas son todas positivas.

max_iterint, default=100

El número de iteraciones de EM a realizar.

n_initint, default=1

El número de inicializaciones a realizar. Se mantiene el resultado con el valor más bajo de la verosimilitud.

init_params{“kmeans”, “random”}, default=”kmeans”

El método utilizado para inicializar las ponderaciones, las medias y las covarianzas. Debe ser uno de los siguientes:

'kmeans' : responsibilities are initialized using kmeans.
'random' : responsibilities are initialized randomly.

weight_concentration_prior_typestr, default=”dirichlet_process”

Cadena que describe el tipo de concentración de ponderaciones a priori. Debe ser uno de los siguientes:

'dirichlet_process' (using the Stick-breaking representation),
'dirichlet_distribution' (can favor more uniform weights).

weight_concentration_priorfloat | None, default=None.

La concentración Dirichlet de cada componente en la distribución de las ponderaciones (Dirichlet). En la literatura se denomina comúnmente gamma. Una mayor concentración pone más masa en el centro y hará que haya más componentes activos, mientras que un parámetro de concentración más bajo hará que haya más masa en el borde simplex de la mezcla de las ponderaciones. El valor del parámetro debe ser mayor que 0. Si es None, se establece en 1 / n_componentes.

mean_precision_priorfloat | None, default=None.

La precisión a priori en la distribución de la media (Gaussiana). Controla el alcance de la ubicación de las medias. Los valores más grandes concentran las medias del conglomerado alrededor de mean_prior. El valor del parámetro debe ser mayor que 0. Si es None, se establece en 1.

mean_priorarray-like, forma (n_features,), default=None.

La a priori de la distribución de la media (Gaussiana). Si es None, se establece en la media de X.

degrees_of_freedom_priorfloat | None, default=None.

La distribución a priori del número de grados de libertad en las distribuciones de covarianza (Wishart). Si es None, se establece en n_features.

covariance_priorflotante o array-like, default=None.

La a priori de la distribución de covarianza (Wishart). Si es None, la a priori de la covarianza empírica se inicializa utilizando la covarianza de X. La forma depende de covariance_type:

(n_features, n_features) if 'full',
(n_features, n_features) if 'tied',
(n_features)             if 'diag',
float                    if 'spherical'

random_stateentero, instancia de RandomState o None, default=None

Controla la semilla aleatoria dada al método elegido para inicializar los parámetros (ver init_params). Además, controla la generación de muestras aleatorias de la distribución ajustada (ver el método sample). Pasa un número entero (int) para una salida reproducible a través de múltiples invocaciones a la función. Ver Glosario.

warm_startbool, default=False

Si “warm_start” es True, la solución del último ajuste se utiliza como inicialización para la siguiente invocación a fit(). Esto puede acelerar la convergencia cuando se invoca a fit varias veces en problemas similares. Ver el Glosario.

verboseint, default=0

Activa la salida verbosa. Si es 1 entonces imprime la inicialización actual y cada paso de iteración. Si es mayor que 1 entonces imprime también la probabilidad logarítmica y el tiempo necesario para cada paso.

verbose_intervalint, default=10

Número de iteraciones realizadas antes de la siguiente impresión.

Atributos

weights_array-like de forma (n_components,)

Las ponderaciones de cada uno de los componentes de la mezcla.

means_array-like de forma (n_components, n_features)

La media de cada componente de la mezcla.

covariances_array-like

La covarianza de cada componente de la mezcla. La forma depende de covariance_type:

(n_components,)                        if 'spherical',
(n_features, n_features)               if 'tied',
(n_components, n_features)             if 'diag',
(n_components, n_features, n_features) if 'full'

precisions_array-like

Las matrices de precisión para cada componente de la mezcla. Una matriz de precisión es la inversa de una matriz de covarianzas. Una matriz de covarianzas es definida simétrica positiva, por lo que la mezcla de Gaussianas puede ser parametrizada equivalentemente por las matrices de precisión. El almacenamiento de las matrices de precisión en lugar de las matrices de covarianzas hace más eficiente el cálculo del logaritmo de la verosimilitud de las nuevas muestras en el momento de la prueba. La forma depende del covariance_type:

(n_components,)                        if 'spherical',
(n_features, n_features)               if 'tied',
(n_components, n_features)             if 'diag',
(n_components, n_features, n_features) if 'full'

precisions_cholesky_array-like

La descomposición de Cholesky de las matrices de precisión de cada componente de la mezcla. Una matriz de precisión es la inversa de una matriz de covarianzas. Una matriz de covarianzas es definida simétrica positiva, por lo que la mezcla de Gaussianas puede ser parametrizada equivalentemente por las matrices de precisión. El almacenamiento de las matrices de precisión en lugar de las matrices de covarianzas hace más eficiente el cálculo del logaritmo de la verosimilitud de las nuevas muestras en el momento de la prueba. La forma depende de covariance_type`:

(n_components,)                        if 'spherical',
(n_features, n_features)               if 'tied',
(n_components, n_features)             if 'diag',
(n_components, n_features, n_features) if 'full'

converged_bool

True cuando se ha alcanzado la convergencia en fit(), False en caso contrario.

n_iter_int

Número de pasos utilizados por el mejor ajuste de inferencia para alcanzar la convergencia.

lower_bound_float

Valor del límite inferior del log-verosimilitud (de los datos de entrenamiento con respecto al modelo) del mejor ajuste de inferencia.

weight_concentration_prior_tupla o float

La concentración de Dirichlet de cada componente en la distribución de las ponderaciones (Dirichlet). El tipo depende de weight_concentration_prior_type:

(float, float) if 'dirichlet_process' (Beta parameters),
float          if 'dirichlet_distribution' (Dirichlet parameters).

Una mayor concentración pone más masa en el centro y hará que haya más componentes activos, mientras que un parámetro de concentración más bajo hará que haya más masa en el borde del simplex.

weight_concentration_array-like de forma (n_components,)

La concentración de Dirichlet de cada componente en la distribución de las ponderaciones (Dirichlet).

mean_precision_prior_float

La precisión a priori en la distribución de la media (Gaussiana). Controla el alcance de la ubicación de las medias. Los valores más grandes concentran las medias del conglomerado alrededor de mean_prior. Si mean_precision_prior se establece en None, mean_precision_prior_ se establece en 1.

mean_precision_array-like de forma (n_components,)

La precisión de cada componente sobre la distribución media (Gaussiana).

mean_prior_array-like de forma (n_features,)

La a priori de la distribución de la media (Gaussiana).

degrees_of_freedom_prior_float

La a priori del número de grados de libertad en las distribuciones de covarianza (Wishart).

degrees_of_freedom_array-like de forma (n_components,)

El número de grados de libertad de cada componente en el modelo.

covariance_prior_float o array-like

La a priori de la distribución de covarianza (Wishart). La forma depende de covariance_type:

(n_features, n_features) if 'full',
(n_features, n_features) if 'tied',
(n_features)             if 'diag',
float                    if 'spherical'

Ver también

GaussianMixture: Ajuste de la mezcla Gaussiana finita con EM.

Referencias

1: Bishop, Christopher M. (2006). «Pattern recognition and machine learning». Vol. 4 No. 4. New York: Springer.
2: Hagai Attias. (2000). «A Variational Bayesian Framework for Graphical Models». In Advances in Neural Information Processing Systems 12.
3: Blei, David M. and Michael I. Jordan. (2006). «Variational inference for Dirichlet process mixtures». Bayesian analysis 1.1

Ejemplos

>>> import numpy as np
>>> from sklearn.mixture import BayesianGaussianMixture
>>> X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [12, 4], [10, 7]])
>>> bgm = BayesianGaussianMixture(n_components=2, random_state=42).fit(X)
>>> bgm.means_
array([[2.49... , 2.29...],
       [8.45..., 4.52... ]])
>>> bgm.predict([[0, 0], [9, 3]])
array([0, 1])

Métodos

`fit`	Estima los parámetros del modelo con el algoritmo EM.
`fit_predict`	Estima los parámetros del modelo utilizando X y predice las etiquetas para X.
`get_params`	Obtiene los parámetros para este estimador.
`predict`	Predice las etiquetas de las muestras de datos en X utilizando el modelo entrenado.
`predict_proba`	Predice la probabilidad a posteriori de cada componente dados los datos.
`sample`	Genera muestras aleatorias a partir de la distribución Gaussiana ajustada.
`score`	Calcula el logaritmo de la verosimilitud promedio por muestra de los datos X dados.
`score_samples`	Calcula las probabilidades logarítmicas ponderadas para cada muestra.
`set_params`	Establece los parámetros de este estimador.

fit()¶

Estima los parámetros del modelo con el algoritmo EM.

El método ajusta el modelo n_init veces y establece los parámetros con los que el modelo tiene la mayor verosimilitud o límite inferior. Dentro de cada ensayo, el método itera entre el paso E y el paso M para max_iter veces hasta que el cambio de la verosimilitud o el límite inferior sea menor que tol, de lo contrario, una ConvergenceWarning se plantea. Si warm_start es True, entonces n_init se ignora y se realiza una única inicialización en la primera invocación. En las invocaciones consecutivas, el entrenamiento comienza donde se dejó.

Parámetros

Xarray-like de forma (n_samples, n_features): Lista de puntos de datos n_features-dimensional. Cada fila corresponde a un único punto de datos.

Devuelve

self

fit_predict()¶

Estima los parámetros del modelo utilizando X y predice las etiquetas para X.

El método ajusta el modelo n_init veces y establece los parámetros con los que el modelo tiene la mayor verosimilitud o límite inferior. Dentro de cada ensayo, el método itera entre el paso E y el paso M para max_iter veces hasta que el cambio de la verosimilitud o el límite inferior es menor que tol, de lo contrario, un ConvergenceWarning se plantea. Después del ajuste, predice la etiqueta más probable para los puntos de datos de entrada.

Nuevo en la versión 0.20.

Parámetros

Xarray-like de forma (n_samples, n_features): Lista de puntos de datos n_features-dimensional. Cada fila corresponde a un único punto de datos.

Devuelve

labelsarreglo, forma (n_samples,): Etiquetas de los componentes.

get_params()¶

Obtiene los parámetros para este estimador.

Parámetros

deepbool, default=True: Si es True, devolverá los parámetros para este estimador y los subobjetos contenidos que son estimadores.

Devuelve

paramsdict: Los nombres de los parámetros mapeados a sus valores.

predict()¶

Predice las etiquetas de las muestras de datos en X utilizando el modelo entrenado.

Parámetros

Xarray-like de forma (n_samples, n_features): Lista de puntos de datos n_features-dimensional. Cada fila corresponde a un único punto de datos.

Devuelve

labelsarreglo, forma (n_samples,): Etiquetas de los componentes.

predict_proba()¶

Predice la probabilidad a posteriori de cada componente dados los datos.

Parámetros

Xarray-like de forma (n_samples, n_features): Lista de puntos de datos n_features-dimensional. Cada fila corresponde a un único punto de datos.

Devuelve

resparreglo, forma (n_samples, n_components): Devuelve la probabilidad de cada Gaussiana (estado) en el modelo dada cada muestra.

sample()¶

Genera muestras aleatorias a partir de la distribución Gaussiana ajustada.

Parámetros

n_samplesint, default=1: Número de muestras a generar.

Devuelve

Xarreglo, forma (n_samples, n_features): Muestra generada aleatoriamente
yarreglo, forma (n_samples,): Etiquetas de los componentes

score()¶

Calcula el logaritmo de la verosimilitud promedio por muestra de los datos X dados.

Parámetros

Xarray-like de forma (n_samples, n_dimensions): Lista de puntos de datos n_features-dimensional. Cada fila corresponde a un único punto de datos.

Devuelve

log_likelihoodfloat: Logaritmo de la verosimilitud de la mezcla Gaussiana dada X.

score_samples()¶

Calcula las probabilidades logarítmicas ponderadas para cada muestra.

Parámetros

Xarray-like de forma (n_samples, n_features): Lista de puntos de datos n_features-dimensional. Cada fila corresponde a un único punto de datos.

Devuelve

log_probarreglo, forma (n_samples,): Probabilidades logarítmicas de cada punto de datos en X.

set_params()¶

Establece los parámetros de este estimador.

El método funciona tanto en estimadores simples como en objetos anidados (como Pipeline). Estos últimos tienen parámetros de la forma <component>__<parameter> para que sea posible actualizar cada componente de un objeto anidado.

Parámetros

**paramsdict: Parámetros del estimador.

Devuelve

selfinstancia de estimador: Instancia del estimador.

Ejemplos utilizando `sklearn.mixture.BayesianGaussianMixture`¶

sklearn.mixture.BayesianGaussianMixture¶

Ejemplos utilizando sklearn.mixture.BayesianGaussianMixture¶

`sklearn.mixture`.BayesianGaussianMixture¶

Ejemplos utilizando `sklearn.mixture.BayesianGaussianMixture`¶