Análisis del Tipo de Concentración a priori de la Variación de Mezcla Gaussiana Bayesiana

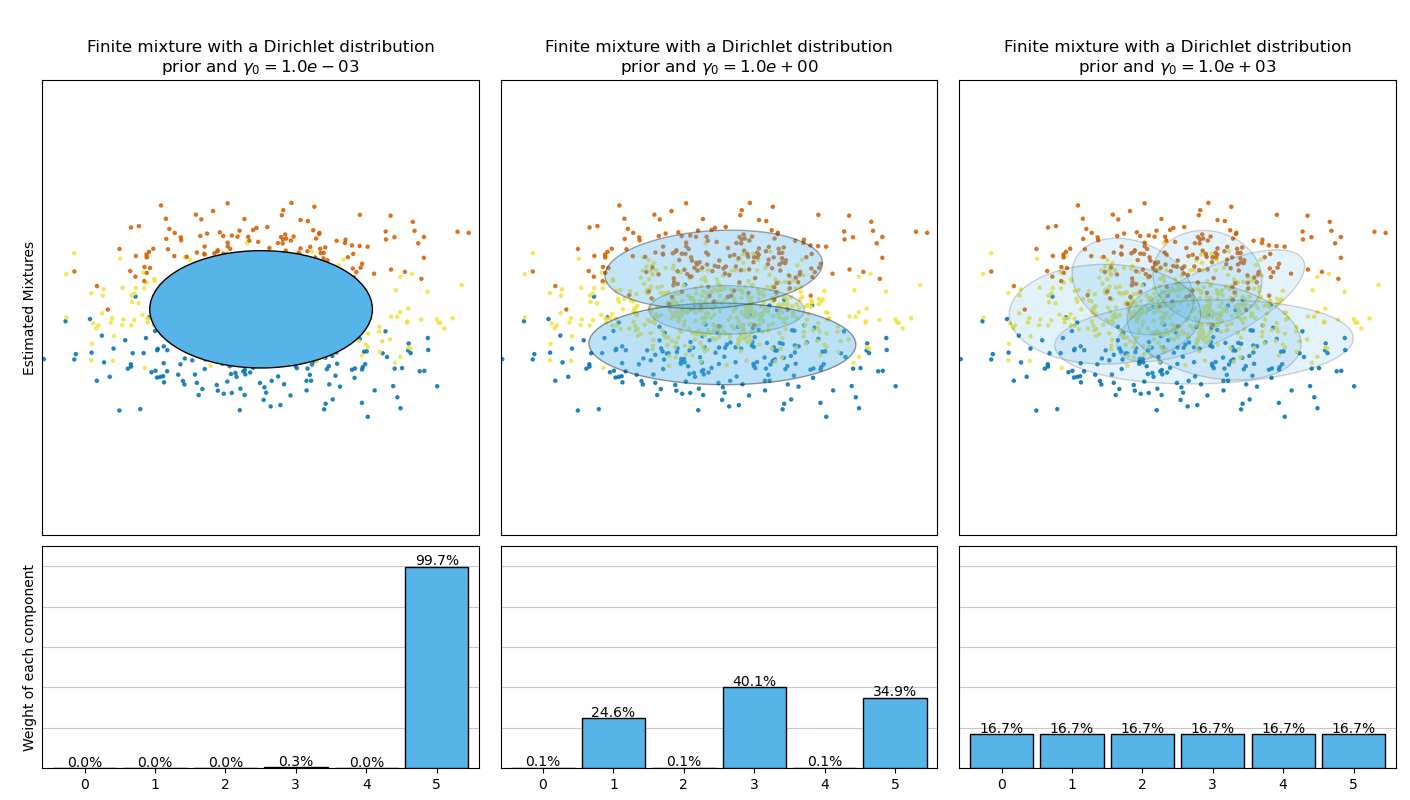
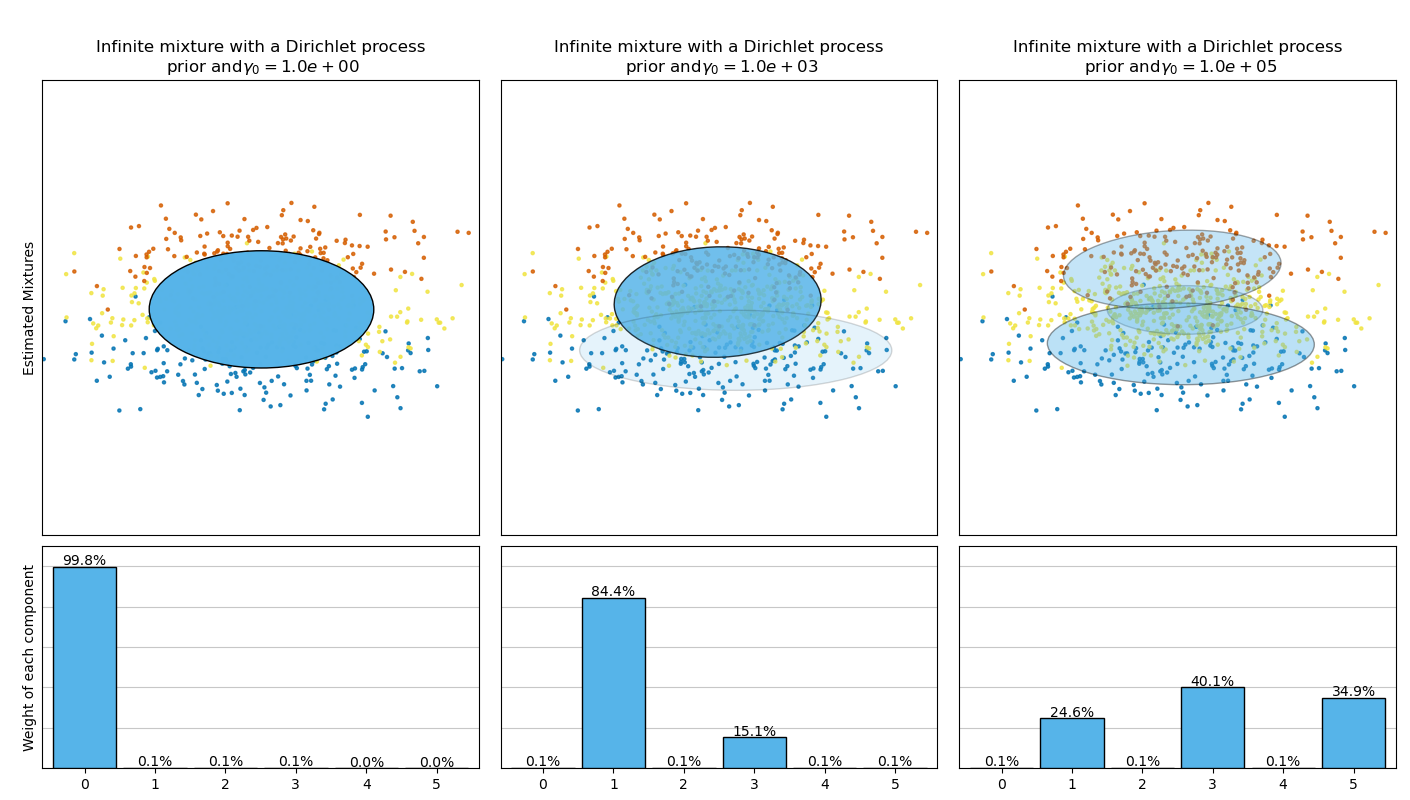
Este ejemplo muestra los elipsoides obtenidos de un conjunto de datos de juguete (mezcla de tres gaussianas) ajustados por los modelos de clase BayesianGaussianMixture con una distribución de Dirichlet a priori (weight_concentration_prior_type='dirichlet_distribution') y un proceso de Dirichlet a priori (weight_concentration_prior_type='dirichlet_process'). En cada figura, representamos los resultados para tres valores diferentes de la concentración de la ponderación a priori.

La clase BayesianGaussianMixture puede adaptar su número de componentes de la mezcla automáticamente. El parámetro weight_concentration_prior tiene una relación directa con el número resultante de componentes con ponderaciones distintas de cero. Especificar un valor bajo para la concentración a priori hará que el modelo ponga la mayor parte de las ponderaciones en pocos componentes y que las ponderaciones de los componentes restantes sean muy cercanas a cero. Los valores altos de la concentración a priori permitirán que un mayor número de componentes estén activos en la mezcla.

El proceso de Dirichlet a priori permite definir un número infinito de componentes y selecciona automáticamente el número correcto de componentes: activa un componente sólo si es necesario.

Por el contrario, el modelo clásico de mezcla finita con una distribución de Dirichlet a priori favorecerá a los componentes más uniformemente ponderados y, por tanto, tiende a dividir los conglomerados naturales en subcomponentes innecesarios.

• 
• 

# Author: Thierry Guillemot <thierry.guillemot.work@gmail.com>
# License: BSD 3 clause

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec

from sklearn.mixture import BayesianGaussianMixture

print(__doc__)


def plot_ellipses(ax, weights, means, covars):
    for n in range(means.shape[0]):
        eig_vals, eig_vecs = np.linalg.eigh(covars[n])
        unit_eig_vec = eig_vecs[0] / np.linalg.norm(eig_vecs[0])
        angle = np.arctan2(unit_eig_vec[1], unit_eig_vec[0])
        # Ellipse needs degrees
        angle = 180 * angle / np.pi
        # eigenvector normalization
        eig_vals = 2 * np.sqrt(2) * np.sqrt(eig_vals)
        ell = mpl.patches.Ellipse(means[n], eig_vals[0], eig_vals[1],
                                  180 + angle, edgecolor='black')
        ell.set_clip_box(ax.bbox)
        ell.set_alpha(weights[n])
        ell.set_facecolor('#56B4E9')
        ax.add_artist(ell)


def plot_results(ax1, ax2, estimator, X, y, title, plot_title=False):
    ax1.set_title(title)
    ax1.scatter(X[:, 0], X[:, 1], s=5, marker='o', color=colors[y], alpha=0.8)
    ax1.set_xlim(-2., 2.)
    ax1.set_ylim(-3., 3.)
    ax1.set_xticks(())
    ax1.set_yticks(())
    plot_ellipses(ax1, estimator.weights_, estimator.means_,
                  estimator.covariances_)

    ax2.get_xaxis().set_tick_params(direction='out')
    ax2.yaxis.grid(True, alpha=0.7)
    for k, w in enumerate(estimator.weights_):
        ax2.bar(k, w, width=0.9, color='#56B4E9', zorder=3,
                align='center', edgecolor='black')
        ax2.text(k, w + 0.007, "%.1f%%" % (w * 100.),
                 horizontalalignment='center')
    ax2.set_xlim(-.6, 2 * n_components - .4)
    ax2.set_ylim(0., 1.1)
    ax2.tick_params(axis='y', which='both', left=False,
                    right=False, labelleft=False)
    ax2.tick_params(axis='x', which='both', top=False)

    if plot_title:
        ax1.set_ylabel('Estimated Mixtures')
        ax2.set_ylabel('Weight of each component')

# Parameters of the dataset
random_state, n_components, n_features = 2, 3, 2
colors = np.array(['#0072B2', '#F0E442', '#D55E00'])

covars = np.array([[[.7, .0], [.0, .1]],
                   [[.5, .0], [.0, .1]],
                   [[.5, .0], [.0, .1]]])
samples = np.array([200, 500, 200])
means = np.array([[.0, -.70],
                  [.0, .0],
                  [.0, .70]])

# mean_precision_prior= 0.8 to minimize the influence of the prior
estimators = [
    ("Finite mixture with a Dirichlet distribution\nprior and "
     r"$\gamma_0=$", BayesianGaussianMixture(
        weight_concentration_prior_type="dirichlet_distribution",
        n_components=2 * n_components, reg_covar=0, init_params='random',
        max_iter=1500, mean_precision_prior=.8,
        random_state=random_state), [0.001, 1, 1000]),
    ("Infinite mixture with a Dirichlet process\n prior and" r"$\gamma_0=$",
     BayesianGaussianMixture(
        weight_concentration_prior_type="dirichlet_process",
        n_components=2 * n_components, reg_covar=0, init_params='random',
        max_iter=1500, mean_precision_prior=.8,
        random_state=random_state), [1, 1000, 100000])]

# Generate data
rng = np.random.RandomState(random_state)
X = np.vstack([
    rng.multivariate_normal(means[j], covars[j], samples[j])
    for j in range(n_components)])
y = np.concatenate([np.full(samples[j], j, dtype=int)
                    for j in range(n_components)])

# Plot results in two different figures
for (title, estimator, concentrations_prior) in estimators:
    plt.figure(figsize=(4.7 * 3, 8))
    plt.subplots_adjust(bottom=.04, top=0.90, hspace=.05, wspace=.05,
                        left=.03, right=.99)

    gs = gridspec.GridSpec(3, len(concentrations_prior))
    for k, concentration in enumerate(concentrations_prior):
        estimator.weight_concentration_prior = concentration
        estimator.fit(X)
        plot_results(plt.subplot(gs[0:2, k]), plt.subplot(gs[2, k]), estimator,
                     X, y, r"%s$%.1e$" % (title, concentration),
                     plot_title=k == 0)

plt.show()