Modelo de Mezcla Gaussiana Curva Sinusoidal

Este ejemplo demuestra el comportamiento de los modelos de mezcla Gaussiana ajustados a datos que no fueron muestreados a partir de una mezcla de variables aleatorias Gaussianas. El conjunto de datos está formado por 100 puntos poco espaciados siguiendo una curva sinusoidal ruidosa. Por lo tanto, no hay un valor de verdad fundamental para el número de componentes Gaussianos.

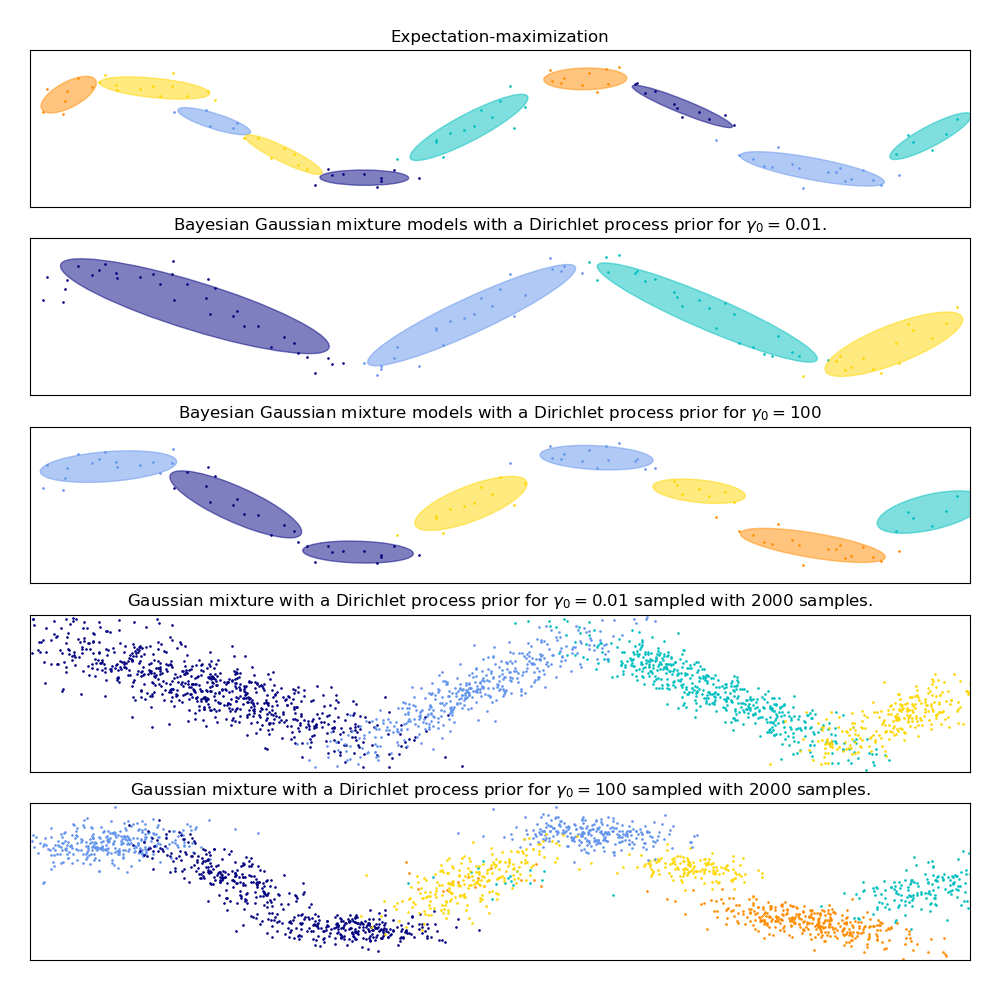
El primer modelo es un modelo clásico de mezcla gaussiana con 10 componentes que se ajusta con el algoritmo de Maximización de la Esperanza.

El segundo modelo es un modelo bayesiano de mezclas con un proceso de Dirichlet a priori ajustado con inferencia variacional. El bajo valor de la concentración a priori hace que el modelo favorezca un menor número de componentes activos. Este modelo «decide» centrar su potencia de modelado en el panorama general de la estructura del conjunto de datos: grupos de puntos con direcciones alternas modelados por matrices de covarianza no diagonales. Esas direcciones alternas capturan a grandes rasgos la naturaleza alternante de la señal sinusoidal original.

El tercer modelo es también un modelo Bayesiano de mezcla Gaussiana con un proceso de Dirichlet a priori, pero esta vez el valor de la concentración a priori es mayor, lo que da al modelo más libertad para modelar la estructura fina de los datos. El resultado es una mezcla con un mayor número de componentes activos que es similar al primer modelo en el que decidimos arbitrariamente fijar el número de componentes en 10.

Qué modelo es el mejor es una cuestión de juicio subjetivo: ¿queremos favorecer los modelos que sólo captan la imagen general para resumir y explicar la mayor parte de la estructura de los datos, ignorando los detalles, o preferimos los modelos que siguen de cerca las regiones de alta densidad de la señal?

Los dos últimos paneles muestran cómo podemos tomar muestras de los dos últimos modelos. Las distribuciones de las muestras resultantes no se parecen exactamente a la distribución original de los datos. La diferencia proviene principalmente del error de aproximación que cometimos al utilizar un modelo que supone que los datos fueron generados por un número finito de componentes Gaussianos en lugar de una curva sinusoidal continua y ruidosa.

import itertools

import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
import matplotlib as mpl

from sklearn import mixture

print(__doc__)

color_iter = itertools.cycle(['navy', 'c', 'cornflowerblue', 'gold',
                              'darkorange'])


def plot_results(X, Y, means, covariances, index, title):
    splot = plt.subplot(5, 1, 1 + index)
    for i, (mean, covar, color) in enumerate(zip(
            means, covariances, color_iter)):
        v, w = linalg.eigh(covar)
        v = 2. * np.sqrt(2.) * np.sqrt(v)
        u = w[0] / linalg.norm(w[0])
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y == i):
            continue
        plt.scatter(X[Y == i, 0], X[Y == i, 1], .8, color=color)

        # Plot an ellipse to show the Gaussian component
        angle = np.arctan(u[1] / u[0])
        angle = 180. * angle / np.pi  # convert to degrees
        ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
        ell.set_clip_box(splot.bbox)
        ell.set_alpha(0.5)
        splot.add_artist(ell)

    plt.xlim(-6., 4. * np.pi - 6.)
    plt.ylim(-5., 5.)
    plt.title(title)
    plt.xticks(())
    plt.yticks(())


def plot_samples(X, Y, n_components, index, title):
    plt.subplot(5, 1, 4 + index)
    for i, color in zip(range(n_components), color_iter):
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y == i):
            continue
        plt.scatter(X[Y == i, 0], X[Y == i, 1], .8, color=color)

    plt.xlim(-6., 4. * np.pi - 6.)
    plt.ylim(-5., 5.)
    plt.title(title)
    plt.xticks(())
    plt.yticks(())


# Parameters
n_samples = 100

# Generate random sample following a sine curve
np.random.seed(0)
X = np.zeros((n_samples, 2))
step = 4. * np.pi / n_samples

for i in range(X.shape[0]):
    x = i * step - 6.
    X[i, 0] = x + np.random.normal(0, 0.1)
    X[i, 1] = 3. * (np.sin(x) + np.random.normal(0, .2))

plt.figure(figsize=(10, 10))
plt.subplots_adjust(bottom=.04, top=0.95, hspace=.2, wspace=.05,
                    left=.03, right=.97)

# Fit a Gaussian mixture with EM using ten components
gmm = mixture.GaussianMixture(n_components=10, covariance_type='full',
                              max_iter=100).fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0,
             'Expectation-maximization')

dpgmm = mixture.BayesianGaussianMixture(
    n_components=10, covariance_type='full', weight_concentration_prior=1e-2,
    weight_concentration_prior_type='dirichlet_process',
    mean_precision_prior=1e-2, covariance_prior=1e0 * np.eye(2),
    init_params="random", max_iter=100, random_state=2).fit(X)
plot_results(X, dpgmm.predict(X), dpgmm.means_, dpgmm.covariances_, 1,
             "Bayesian Gaussian mixture models with a Dirichlet process prior "
             r"for $\gamma_0=0.01$.")

X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(X_s, y_s, dpgmm.n_components, 0,
             "Gaussian mixture with a Dirichlet process prior "
             r"for $\gamma_0=0.01$ sampled with $2000$ samples.")

dpgmm = mixture.BayesianGaussianMixture(
    n_components=10, covariance_type='full', weight_concentration_prior=1e+2,
    weight_concentration_prior_type='dirichlet_process',
    mean_precision_prior=1e-2, covariance_prior=1e0 * np.eye(2),
    init_params="kmeans", max_iter=100, random_state=2).fit(X)
plot_results(X, dpgmm.predict(X), dpgmm.means_, dpgmm.covariances_, 2,
             "Bayesian Gaussian mixture models with a Dirichlet process prior "
             r"for $\gamma_0=100$")

X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(X_s, y_s, dpgmm.n_components, 1,
             "Gaussian mixture with a Dirichlet process prior "
             r"for $\gamma_0=100$ sampled with $2000$ samples.")

plt.show()