Elipsoides del Modelo de Mezcla Gaussiana

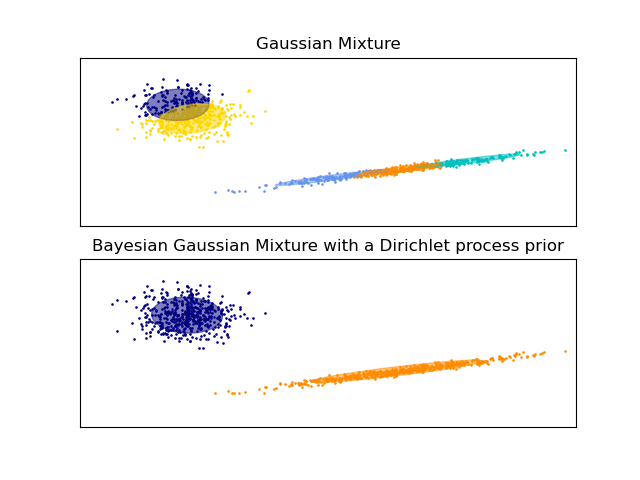
Gráfica los elipsoides de confianza de una mezcla de dos Gaussianas obtenidos con la Maximización de la Esperanza (clase GaussianMixture) y la Inferencia Variacional (modelos de clase BayesianGaussianMixture con un proceso Dirichlet a priori).

Ambos modelos tienen acceso a cinco componentes con los que ajustar los datos. Ten en cuenta que el modelo de Maximización de la Esperanza utilizará necesariamente los cinco componentes, mientras que el modelo de Inferencia Variacional sólo utilizará los que sean necesarios para un buen ajuste. Aquí podemos ver que el modelo de Maximización de la Esperanza divide algunos componentes arbitrariamente, porque está tratando de ajustar demasiados componentes, mientras que el modelo de Proceso Dirichlet adapta su número de estado automáticamente.

Este ejemplo no lo muestra, ya que estamos en un espacio de baja dimensión, pero otra ventaja del modelo de proceso de Dirichlet es que puede ajustar matrices de covarianza completas de forma efectiva incluso cuando hay menos ejemplos por conglomerados que dimensiones en los datos, debido a las propiedades de regularización del algoritmo de inferencia.

import itertools

import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
import matplotlib as mpl

from sklearn import mixture

color_iter = itertools.cycle(['navy', 'c', 'cornflowerblue', 'gold',
                              'darkorange'])


def plot_results(X, Y_, means, covariances, index, title):
    splot = plt.subplot(2, 1, 1 + index)
    for i, (mean, covar, color) in enumerate(zip(
            means, covariances, color_iter)):
        v, w = linalg.eigh(covar)
        v = 2. * np.sqrt(2.) * np.sqrt(v)
        u = w[0] / linalg.norm(w[0])
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y_ == i):
            continue
        plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], .8, color=color)

        # Plot an ellipse to show the Gaussian component
        angle = np.arctan(u[1] / u[0])
        angle = 180. * angle / np.pi  # convert to degrees
        ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
        ell.set_clip_box(splot.bbox)
        ell.set_alpha(0.5)
        splot.add_artist(ell)

    plt.xlim(-9., 5.)
    plt.ylim(-3., 6.)
    plt.xticks(())
    plt.yticks(())
    plt.title(title)


# Number of samples per component
n_samples = 500

# Generate random sample, two components
np.random.seed(0)
C = np.array([[0., -0.1], [1.7, .4]])
X = np.r_[np.dot(np.random.randn(n_samples, 2), C),
          .7 * np.random.randn(n_samples, 2) + np.array([-6, 3])]

# Fit a Gaussian mixture with EM using five components
gmm = mixture.GaussianMixture(n_components=5, covariance_type='full').fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0,
             'Gaussian Mixture')

# Fit a Dirichlet process Gaussian mixture using five components
dpgmm = mixture.BayesianGaussianMixture(n_components=5,
                                        covariance_type='full').fit(X)
plot_results(X, dpgmm.predict(X), dpgmm.means_, dpgmm.covariances_, 1,
             'Bayesian Gaussian Mixture with a Dirichlet process prior')

plt.show()