Imputar valores faltantes antes de crear un estimador

Los valores faltantes pueden ser reemplazados por la media, la mediana o el valor más frecuente usando el básico SimpleImputer.

En este ejemplo investigaremos diferentes técnicas de imputación:

• imputación por el valor constante 0

• imputación por el valor medio de cada característica combinada con una variable auxiliar indicadora de ausencia

• k imputación del vecino más cercano

• imputación iterativa

Utilizaremos dos conjuntos de datos: el conjunto de datos de diabetes que consiste en 10 variables de características recolectadas de pacientes con diabetes con el objetivo de predecir la progresión de la enfermedad y el conjunto de datos de California Housing para el cual el objetivo es la mediana del valor de la casa de los distritos de California.

Como ninguno de estos conjuntos de datos tiene valores faltantes, eliminaremos algunos valores para crear nuevas versiones con datos artificialmente faltantes. El rendimiento de RandomForestRegressor en el conjunto de datos original se compara entonces el rendimiento en los conjuntos de datos alterados con los valores artificialmente faltantes imputados utilizando diferentes técnicas.

print(__doc__)

# Authors: Maria Telenczuk  <https://github.com/maikia>
# License: BSD 3 clause

Descargar los datos y hacer conjuntos de valores faltantes

Primero descargamos los dos conjuntos de datos. El conjunto de datos de diabetes se envía con scikit-learn. Tiene 442 entradas, cada una con 10 características. El conjunto de datos de California Housing es mucho más grande con 20640 entradas y 8 características. Es necesario descargarlo. Sólo utilizaremos las primeras 400 entradas con el fin de acelerar los cálculos, pero no dudes en utilizar todo el conjunto de datos.

import numpy as np

from sklearn.datasets import fetch_california_housing
from sklearn.datasets import load_diabetes


rng = np.random.RandomState(42)

X_diabetes, y_diabetes = load_diabetes(return_X_y=True)
X_california, y_california = fetch_california_housing(return_X_y=True)
X_california = X_california[:400]
y_california = y_california[:400]


def add_missing_values(X_full, y_full):
    n_samples, n_features = X_full.shape

    # Add missing values in 75% of the lines
    missing_rate = 0.75
    n_missing_samples = int(n_samples * missing_rate)

    missing_samples = np.zeros(n_samples, dtype=bool)
    missing_samples[: n_missing_samples] = True

    rng.shuffle(missing_samples)
    missing_features = rng.randint(0, n_features, n_missing_samples)
    X_missing = X_full.copy()
    X_missing[missing_samples, missing_features] = np.nan
    y_missing = y_full.copy()

    return X_missing, y_missing


X_miss_california, y_miss_california = add_missing_values(
    X_california, y_california)

X_miss_diabetes, y_miss_diabetes = add_missing_values(
    X_diabetes, y_diabetes)

Imputar los datos que faltan y la puntuación

Ahora vamos a escribir una función que marcará los resultados en los datos diferentes imputados. Veamos cada imputador por separado:

rng = np.random.RandomState(0)

from sklearn.ensemble import RandomForestRegressor

# To use the experimental IterativeImputer, we need to explicitly ask for it:
from sklearn.experimental import enable_iterative_imputer  # noqa
from sklearn.impute import SimpleImputer, KNNImputer, IterativeImputer
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline


N_SPLITS = 5
regressor = RandomForestRegressor(random_state=0)

Información faltante

Además de imputar los valores faltantes, los imputadores tienen un parámetro add_indicator que marca los valores que faltan, que pueden llevar alguna información.

def get_scores_for_imputer(imputer, X_missing, y_missing):
    estimator = make_pipeline(imputer, regressor)
    impute_scores = cross_val_score(estimator, X_missing, y_missing,
                                    scoring='neg_mean_squared_error',
                                    cv=N_SPLITS)
    return impute_scores


x_labels = ['Full data',
            'Zero imputation',
            'Mean Imputation',
            'KNN Imputation',
            'Iterative Imputation']

mses_california = np.zeros(5)
stds_california = np.zeros(5)
mses_diabetes = np.zeros(5)
stds_diabetes = np.zeros(5)

Estimar la puntuación

En primer lugar, queremos estimar la puntuación en los datos originales:

def get_full_score(X_full, y_full):
    full_scores = cross_val_score(regressor, X_full, y_full,
                                  scoring='neg_mean_squared_error',
                                  cv=N_SPLITS)
    return full_scores.mean(), full_scores.std()


mses_california[0], stds_california[0] = get_full_score(X_california,
                                                        y_california)
mses_diabetes[0], stds_diabetes[0] = get_full_score(X_diabetes, y_diabetes)

Reemplaza valores faltantes por 0

Ahora calcularemos la puntuación en los datos donde los valores faltantes son reemplazados por 0:

def get_impute_zero_score(X_missing, y_missing):

    imputer = SimpleImputer(missing_values=np.nan, add_indicator=True,
                            strategy='constant', fill_value=0)
    zero_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)
    return zero_impute_scores.mean(), zero_impute_scores.std()


mses_california[1], stds_california[1] = get_impute_zero_score(
    X_miss_california, y_miss_california)
mses_diabetes[1], stds_diabetes[1] = get_impute_zero_score(X_miss_diabetes,
                                                           y_miss_diabetes)

Imputación kNN de los valores faltantes

KNNImputer imputa valores faltantes usando la media ponderada o no ponderada del número deseado de vecinos más cercanos.

def get_impute_knn_score(X_missing, y_missing):
    imputer = KNNImputer(missing_values=np.nan, add_indicator=True)
    knn_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)
    return knn_impute_scores.mean(), knn_impute_scores.std()


mses_california[2], stds_california[2] = get_impute_knn_score(
    X_miss_california, y_miss_california)
mses_diabetes[2], stds_diabetes[2] = get_impute_knn_score(X_miss_diabetes,
                                                          y_miss_diabetes)

Imputa valores faltantes con media

def get_impute_mean(X_missing, y_missing):
    imputer = SimpleImputer(missing_values=np.nan, strategy="mean",
                            add_indicator=True)
    mean_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)
    return mean_impute_scores.mean(), mean_impute_scores.std()


mses_california[3], stds_california[3] = get_impute_mean(X_miss_california,
                                                         y_miss_california)
mses_diabetes[3], stds_diabetes[3] = get_impute_mean(X_miss_diabetes,
                                                     y_miss_diabetes)

Imputación iterativa de los valores faltantes

Otra opción es la IterativeImputer. Esta utiliza la regresión lineal round-robin, modelando cada característica con valores faltantes como una función de otras características, a su vez. La versión implementada asume variables gaussianas (de salida). Si tus características son obviamente no normales, considera la posibilidad de transformarlas para que parezcan más normales para mejorar potencialmente el rendimiento.

def get_impute_iterative(X_missing, y_missing):
    imputer = IterativeImputer(missing_values=np.nan, add_indicator=True,
                               random_state=0, n_nearest_features=5,
                               sample_posterior=True)
    iterative_impute_scores = get_scores_for_imputer(imputer,
                                                     X_missing,
                                                     y_missing)
    return iterative_impute_scores.mean(), iterative_impute_scores.std()


mses_california[4], stds_california[4] = get_impute_iterative(
    X_miss_california, y_miss_california)
mses_diabetes[4], stds_diabetes[4] = get_impute_iterative(X_miss_diabetes,
                                                          y_miss_diabetes)

mses_diabetes = mses_diabetes * -1
mses_california = mses_california * -1

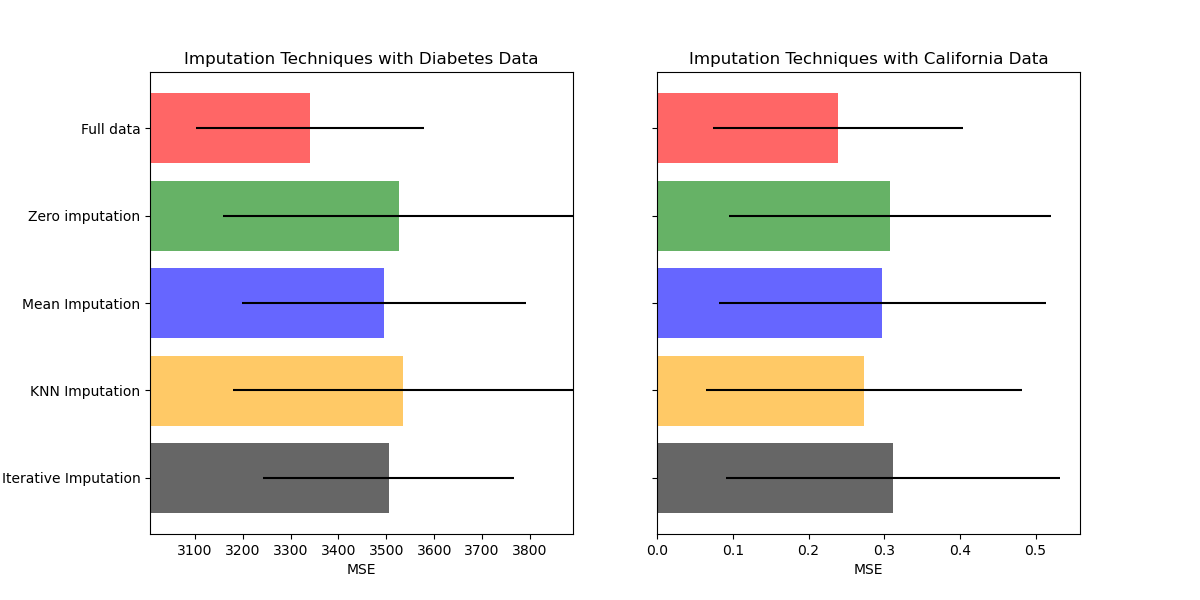
Traza los resultados

Finalmente vamos a visualizar la puntuación:

import matplotlib.pyplot as plt


n_bars = len(mses_diabetes)
xval = np.arange(n_bars)

colors = ['r', 'g', 'b', 'orange', 'black']

# plot diabetes results
plt.figure(figsize=(12, 6))
ax1 = plt.subplot(121)
for j in xval:
    ax1.barh(j, mses_diabetes[j], xerr=stds_diabetes[j],
             color=colors[j], alpha=0.6, align='center')

ax1.set_title('Imputation Techniques with Diabetes Data')
ax1.set_xlim(left=np.min(mses_diabetes) * 0.9,
             right=np.max(mses_diabetes) * 1.1)
ax1.set_yticks(xval)
ax1.set_xlabel('MSE')
ax1.invert_yaxis()
ax1.set_yticklabels(x_labels)

# plot california dataset results
ax2 = plt.subplot(122)
for j in xval:
    ax2.barh(j, mses_california[j], xerr=stds_california[j],
             color=colors[j], alpha=0.6, align='center')

ax2.set_title('Imputation Techniques with California Data')
ax2.set_yticks(xval)
ax2.set_xlabel('MSE')
ax2.invert_yaxis()
ax2.set_yticklabels([''] * n_bars)

plt.show()

# You can also try different techniques. For instance, the median is a more
# robust estimator for data with high magnitude variables which could dominate
# results (otherwise known as a 'long tail').