3.4. Curvas de validación: dibujar las puntuaciones para evaluar los modelos¶
Cada estimador tiene sus ventajas e inconvenientes. Su error de generalización puede descomponerse en términos de sesgo, varianza y ruido. El sesgo de un estimador es su error medio para diferentes conjuntos de entrenamiento. La varianza de un estimador indica su sensibilidad a la variación de los conjuntos de entrenamiento. El ruido es una propiedad de los datos.
En el siguiente gráfico, vemos una función \(f(x) = \cos (\frac{3}{2} \pi x)\) y algunas muestras ruidosas de esa función. Utilizamos tres estimadores diferentes para ajustar la función: regresión lineal con características polinómicas de grado 1, 4 y 15. Vemos que el primer estimador sólo puede proporcionar, en el mejor de los casos, un ajuste pobre a las muestras y a la función verdadera porque es demasiado simple (alto sesgo), el segundo estimador se aproxima casi perfectamente y el último estimador se aproxima perfectamente a los datos de entrenamiento pero no se ajusta muy bien a la función verdadera, es decir, es muy sensible a la variación de los datos de entrenamiento (alta varianza).
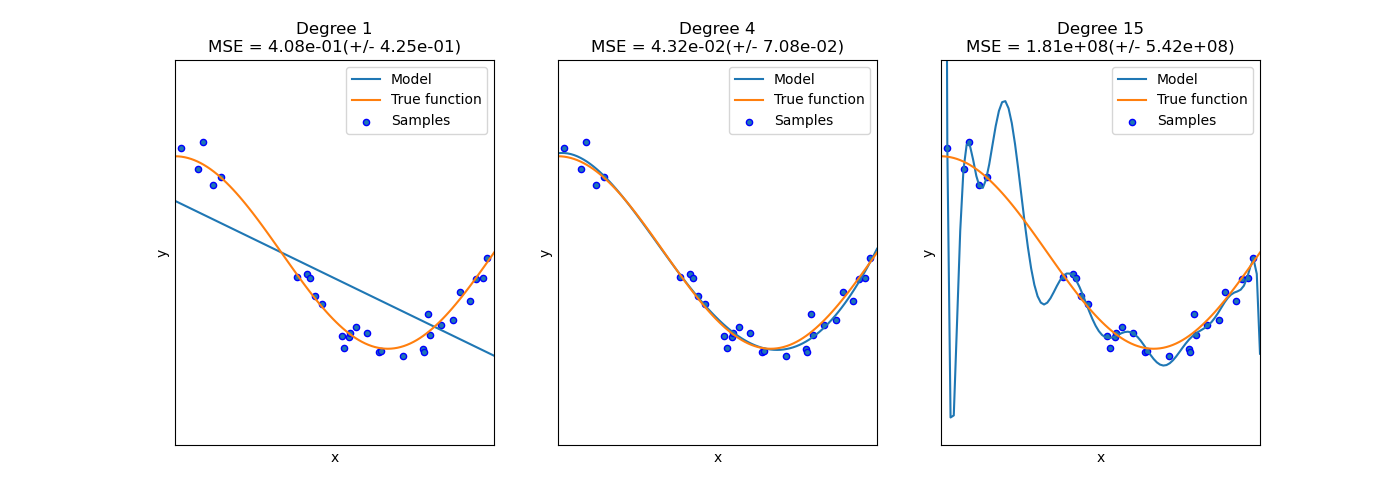
El sesgo y la varianza son propiedades inherentes a los estimadores y, por lo general, tenemos que seleccionar los algoritmos de aprendizaje y los hiperparámetros para que tanto el sesgo como la varianza sean lo más bajos posible (ver el dilema Bias-varianza). Otra forma de reducir la varianza de un modelo es utilizar más datos de entrenamiento. Sin embargo, sólo debería recoger más datos de entrenamiento si la función verdadera es demasiado compleja para ser aproximada por un estimador con una varianza menor.
En el problema unidimensional sencillo que hemos visto en el ejemplo es fácil ver si el estimador sufre de sesgo o varianza. Sin embargo, en espacios de alta dimensión, los modelos pueden resultar muy difíciles de visualizar. Por este motivo, suele ser útil utilizar las herramientas que se describen a continuación.
3.4.1. Curva de validación¶
Para validar un modelo necesitamos una función de puntuación (ver Métricas y puntuación: cuantificar la calidad de las predicciones), por ejemplo la exactitud de los clasificadores. La forma adecuada de elegir múltiples hiperparámetros de un estimador es, por supuesto, la búsqueda en cuadrícula o métodos similares (ver Ajustar los hiperparámetros de un estimador) que seleccionan el hiperparámetro con la máxima puntuación en un conjunto de validación o en múltiples conjuntos de validación. Ten en cuenta que si optimizamos los hiperparámetros basándonos en una puntuación de validación, la puntuación de validación está sesgada y ya no es una buena estimación de la generalización. Para obtener una estimación adecuada de la generalización tenemos que calcular la puntuación en otro conjunto de pruebas.
Sin embargo, a veces es útil dibujar la influencia de un solo hiperparámetro en la puntuación de entrenamiento y en la puntuación de validación para averiguar si el estimador está sobreajustado o infraajustado para algunos valores del hiperparámetro.
La función validation_curve puede ayudar en este caso:
>>> import numpy as np
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import Ridge
>>> np.random.seed(0)
>>> X, y = load_iris(return_X_y=True)
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]
>>> train_scores, valid_scores = validation_curve(Ridge(), X, y, "alpha",
... np.logspace(-7, 3, 3),
... cv=5)
>>> train_scores
array([[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.51..., 0.52..., 0.49..., 0.47..., 0.49...]])
>>> valid_scores
array([[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.46..., 0.25..., 0.50..., 0.49..., 0.52...]])
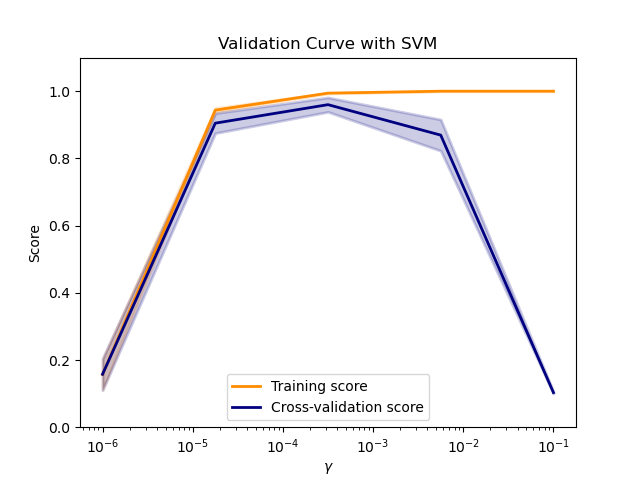
Si la puntuación de entrenamiento y la de validación son bajas, el estimador estará infra ajustado. Si la puntuación de entrenamiento es alta y la de validación es baja, el estimador está sobre ajustado y, por el contrario, funciona muy bien. Una puntuación de entrenamiento baja y una puntuación de validación alta no suelen ser posibles. La infra adaptación, la sobre adaptación y un modelo que funciona se muestran en el gráfico siguiente, en el que variamos el parámetro \(\gamma\) de una SVM en el conjunto de datos de dígitos.
3.4.2. Curva de aprendizaje¶
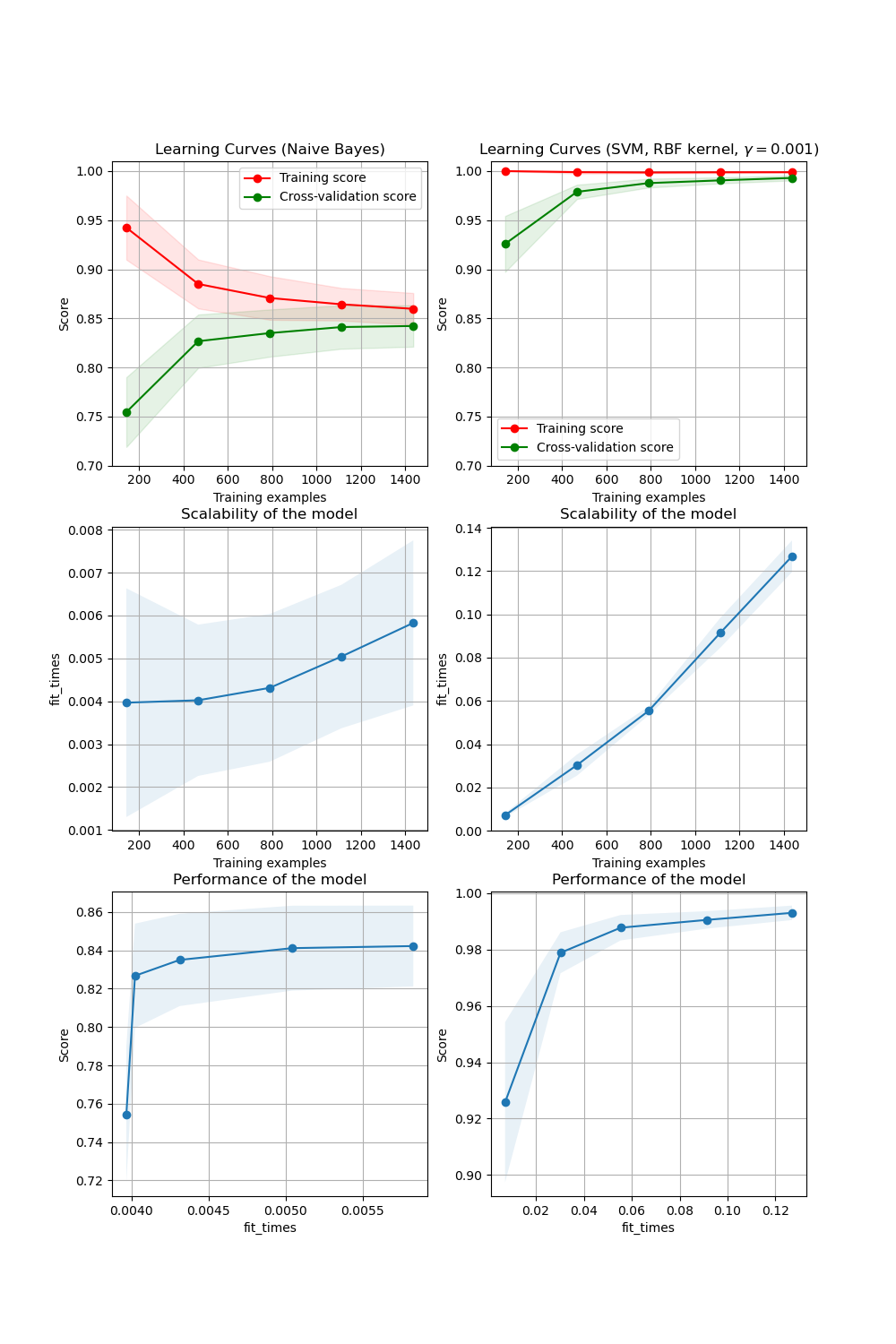
Una curva de aprendizaje muestra la puntuación de validación y entrenamiento de un estimador para un número variable de muestras de entrenamiento. Es una herramienta para averiguar cuánto nos beneficiamos al añadir más datos de entrenamiento y si el estimador sufre más un error de varianza o un error de sesgo. Consideremos el siguiente ejemplo, en el que trazamos la curva de aprendizaje de un clasificador bayesiano ingenuo y un SVM.
Para el bayesiano ingenuo, tanto la puntuación de validación como la de entrenamiento convergen a un valor que es bastante bajo con el aumento del tamaño del conjunto de entrenamiento. Por lo tanto, es probable que no nos beneficiemos mucho de más datos de entrenamiento.
En cambio, para pequeñas cantidades de datos, la puntuación de entrenamiento de la SVM es mucho mayor que la de validación. Si se añaden más muestras de entrenamiento, lo más probable es que aumente la generalización.
Podemos utilizar la función learning_curve para generar los valores necesarios para dibujar dicha curva de aprendizaje (número de muestras que se han utilizado, las puntuaciones medias en los conjuntos de entrenamiento y las puntuaciones medias en los conjuntos de validación):
>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC
>>> train_sizes, train_scores, valid_scores = learning_curve(
... SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes
array([ 50, 80, 110])
>>> train_scores
array([[0.98..., 0.98 , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.99...]])
>>> valid_scores
array([[1. , 0.93..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...]])
