Comparación de pruebas F e información mutua

Este ejemplo ilustra las diferencias entre estadísticas univariadas de pruebas F e información mutua.

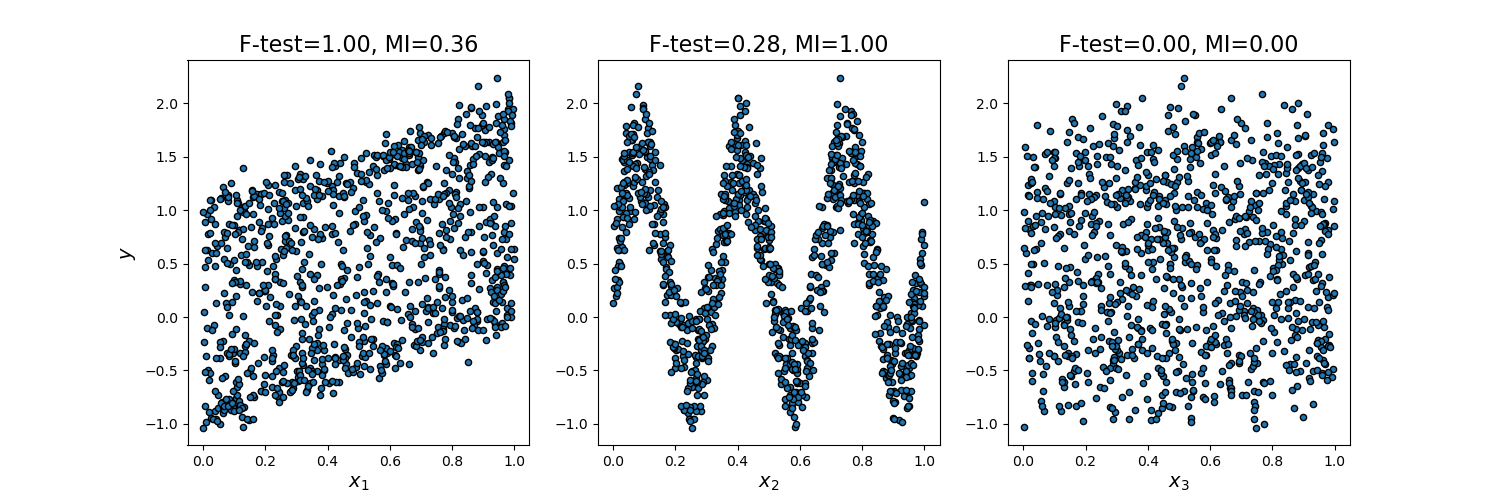
Consideramos 3 características x_1, x_2, x_3 distribuidas uniformemente sobre [0, 1], el objetivo depende de ellas de la siguiente manera:

y = x_1 + sin(6 * pi * x_2) + 0.1 * N(0, 1), que es la tercera característica es completamente irrelevante.

El código siguiente traza la dependencia de y frente a x_i individual y los valores normalizados de estadísticas univariadas de F-tests e información mutua.

Como la prueba F sólo capta la dependencia lineal, califica a x_1 como la característica más discriminativa. Por otro lado, la información mutua puede capturar cualquier tipo de dependencia entre las variables y califica a x_2 como la característica más discriminatoria, lo que probablemente concuerda mejor con nuestra percepción intuitiva para este ejemplo. Ambos métodos marcan correctamente x_3 como irrelevante.

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_selection import f_regression, mutual_info_regression

np.random.seed(0)
X = np.random.rand(1000, 3)
y = X[:, 0] + np.sin(6 * np.pi * X[:, 1]) + 0.1 * np.random.randn(1000)

f_test, _ = f_regression(X, y)
f_test /= np.max(f_test)

mi = mutual_info_regression(X, y)
mi /= np.max(mi)

plt.figure(figsize=(15, 5))
for i in range(3):
    plt.subplot(1, 3, i + 1)
    plt.scatter(X[:, i], y, edgecolor='black', s=20)
    plt.xlabel("$x_{}$".format(i + 1), fontsize=14)
    if i == 0:
        plt.ylabel("$y$", fontsize=14)
    plt.title("F-test={:.2f}, MI={:.2f}".format(f_test[i], mi[i]),
              fontsize=16)
plt.show()