sklearn.feature_selection.mutual_info_regression¶
- sklearn.feature_selection.mutual_info_regression()¶
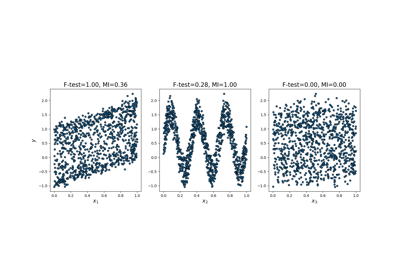
Estimar la información mutua para una variable objetivo continua.
La información mutua (IM) [1] entre dos variables aleatorias es un valor no negativo que mide la dependencia entre las variables. Es igual a cero si y sólo si dos variables aleatorias son independientes, y los valores más altos significan una mayor dependencia.
La función se basa en métodos no paramétricos basados en la estimación de la entropía a partir de las distancias k- vecinos más cercanos, como se describe en [2] y [3]. Ambos métodos se basan en la idea propuesta originalmente en [4].
Puede utilizarse para la selección de características univariantes, lee más en el Manual de usuario.
- Parámetros
- Xarray-like o matriz dispersa, de forma (n_samples, n_features)
Matriz de características.
- yarray-like de forma (n_samples,)
Vector objetivo.
- discrete_features{“auto”, bool, array-like}, default=”auto”
Si es bool, entonces determina si se consideran todas las características discretas o continuas. Si es un array, entonces debe ser una máscara booleana con forma (n_características,) o un arreglo con índices de características discretas. Si es “auto”, se asigna a False para
Xdenso y a True paraXdisperso.- n_neighborsint, default=3
Número de vecinos a utilizar para la estimación de la IM para variables continuas, ver [2] y [3]. Los valores más altos reducen la varianza de la estimación, pero podrían introducir un sesgo.
- copybooleano, default=True
Si se hace una copia de los datos dados. Si se establece en False, los datos iniciales se sobrescribirán.
- random_stateentero, instancia de RandomState o None, default=None
Determina la generación de números aleatorios para añadir un pequeño ruido a las variables continuas con el fin de eliminar los valores repetidos. Pasa un int para obtener resultados reproducibles a través de múltiples llamadas a la función. Ver Glosario.
- Devuelve
- mindarray de forma (n_features,)
Información mutua estimada entre cada característica y el objetivo.
Notas
Se utiliza el término «características discretas» en lugar de denominarlas «categóricas», porque describe la esencia con mayor precisión. Por ejemplo, las intensidades de los píxeles de una imagen son características discretas (pero difícilmente categóricas) y obtendrás mejores resultados si las marca como tales. Ten en cuenta también que tratar una variable continua como discreta y viceversa suele dar resultados incorrectos, así que esté atento a ello.
La información mutua verdadera no puede ser negativa. Si su estimación resulta negativa, se sustituye por cero.
Referencias
- 1
Información Mutua en Wikipedia.
- 2(1,2)
A. Kraskov, H. Stogbauer and P. Grassberger, «Estimating mutual information». Phys. Rev. E 69, 2004.
- 3(1,2)
B. C. Ross «Mutual Information between Discrete and Continuous Data Sets». PLoS ONE 9(2), 2014.
- 4
L. F. Kozachenko, N. N. Leonenko, «Sample Estimate of the Entropy of a Random Vector», Probl. Peredachi Inf., 23:2 (1987), 9-16