Análisis factorial (con rotación) para visualizar patrones

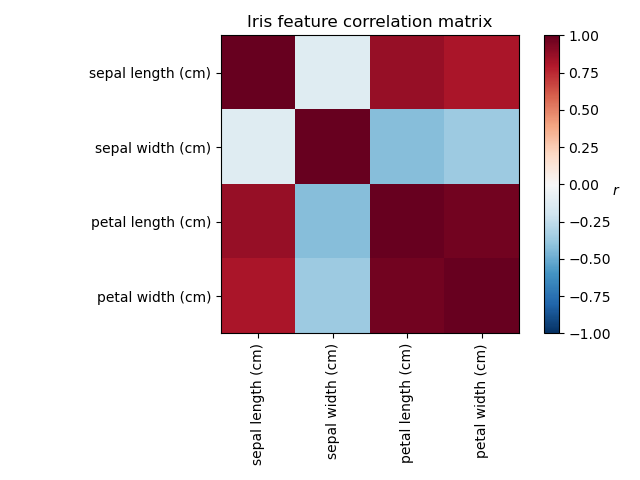
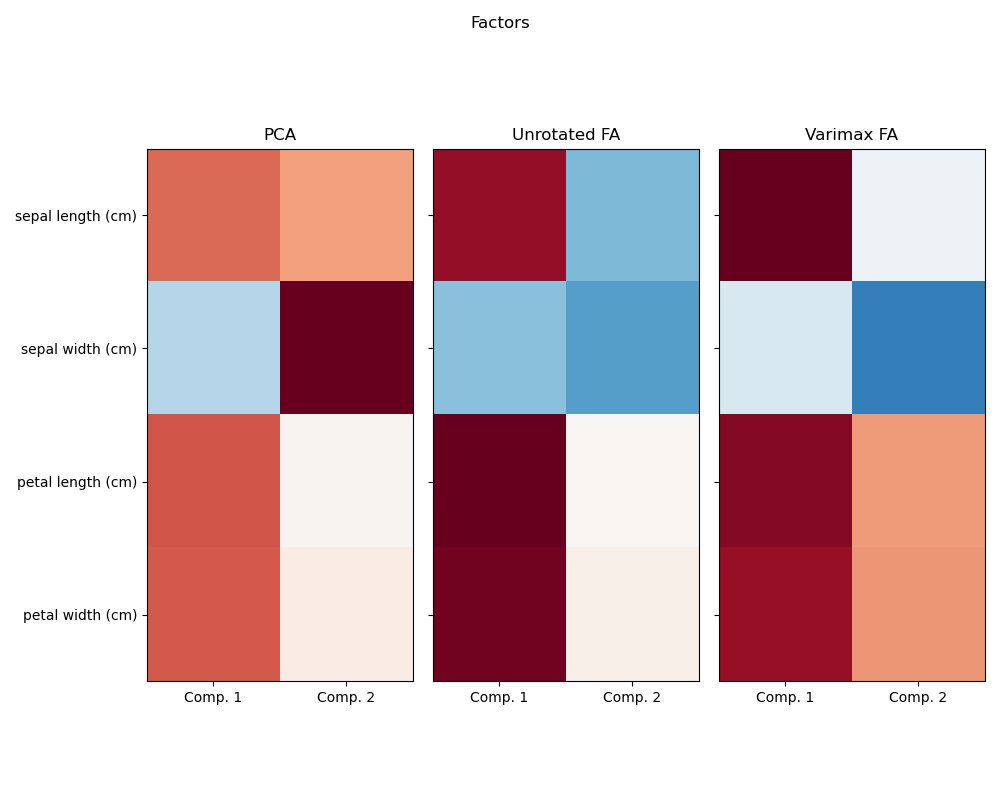
Al investigar el conjunto de datos de Iris, vemos que la longitud de los sépalos, la longitud de los pétalos y la anchura de los pétalos están muy correlacionados. La anchura de los sépalos es menos redundante. Las técnicas de descomposición de matrices pueden descubrir estos patrones latentes. La aplicación de rotaciones a los componentes resultantes no mejora intrínsecamente el valor predictivo del espacio latente derivado, pero puede ayudar a visualizar su estructura; aquí, por ejemplo, la rotación varimax, que se encuentra maximizando las varianzas al cuadrado de los pesos, encuentra una estructura en la que el segundo componente sólo se carga positivamente en la anchura del sépalo.

# Authors: Jona Sassenhagen
# License: BSD 3 clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.decomposition import FactorAnalysis, PCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris

print(__doc__)

Carga datos de Iris

data = load_iris()
X = StandardScaler().fit_transform(data["data"])
feature_names = data["feature_names"]

Grafica la covarianza de las características del Iris

ax = plt.axes()

im = ax.imshow(np.corrcoef(X.T), cmap="RdBu_r", vmin=-1, vmax=1)

ax.set_xticks([0, 1, 2, 3])
ax.set_xticklabels(list(feature_names), rotation=90)
ax.set_yticks([0, 1, 2, 3])
ax.set_yticklabels(list(feature_names))

plt.colorbar(im).ax.set_ylabel("$r$", rotation=0)
ax.set_title("Iris feature correlation matrix")
plt.tight_layout()

Realiza un análisis factorial con rotación Varimax

n_comps = 2

methods = [('PCA', PCA()),
           ('Unrotated FA', FactorAnalysis()),
           ('Varimax FA', FactorAnalysis(rotation='varimax'))]
fig, axes = plt.subplots(ncols=len(methods), figsize=(10, 8))

for ax, (method, fa) in zip(axes, methods):
    fa.set_params(n_components=n_comps)
    fa.fit(X)

    components = fa.components_.T
    print("\n\n %s :\n" % method)
    print(components)

    vmax = np.abs(components).max()
    ax.imshow(components, cmap="RdBu_r", vmax=vmax, vmin=-vmax)
    ax.set_yticks(np.arange(len(feature_names)))
    if ax.is_first_col():
        ax.set_yticklabels(feature_names)
    else:
        ax.set_yticklabels([])
    ax.set_title(str(method))
    ax.set_xticks([0, 1])
    ax.set_xticklabels(["Comp. 1", "Comp. 2"])
fig.suptitle("Factors")
plt.tight_layout()
plt.show()

Out:

 PCA :

[[ 0.52106591  0.37741762]
 [-0.26934744  0.92329566]
 [ 0.5804131   0.02449161]
 [ 0.56485654  0.06694199]]


 Unrotated FA :

[[ 0.88096009 -0.4472869 ]
 [-0.41691605 -0.55390036]
 [ 0.99918858  0.01915283]
 [ 0.96228895  0.05840206]]


 Varimax FA :

[[ 0.98633022 -0.05752333]
 [-0.16052385 -0.67443065]
 [ 0.90809432  0.41726413]
 [ 0.85857475  0.43847489]]