Separación ciega de fuentes mediante FastICA

Un ejemplo de estimación de fuentes a partir de datos ruidosos.

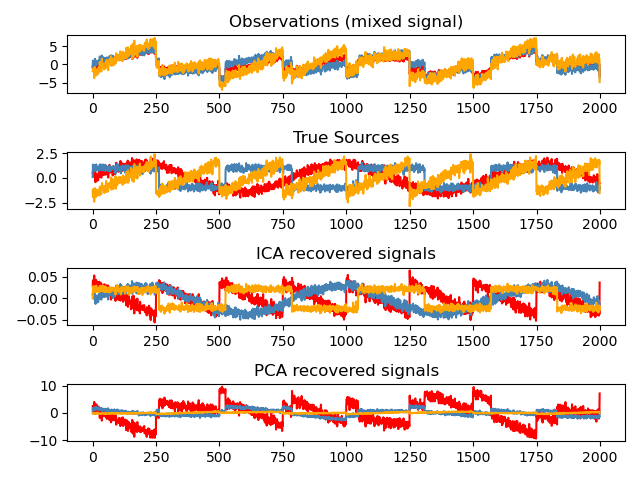
Análisis de componentes independientes (ICA) se utiliza para estimar las fuentes dadas las mediciones ruidosas. Imagina 3 instrumentos tocando simultáneamente y 3 micrófonos grabando las señales mezcladas. ICA se utiliza para recuperar las fuentes, es decir, lo que toca cada instrumento. Es importante destacar que PCA no consigue recuperar nuestros instruments, ya que las señales relacionadas reflejan procesos no gaussianos.

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

from sklearn.decomposition import FastICA, PCA

# #############################################################################
# Generate sample data
np.random.seed(0)
n_samples = 2000
time = np.linspace(0, 8, n_samples)

s1 = np.sin(2 * time)  # Signal 1 : sinusoidal signal
s2 = np.sign(np.sin(3 * time))  # Signal 2 : square signal
s3 = signal.sawtooth(2 * np.pi * time)  # Signal 3: saw tooth signal

S = np.c_[s1, s2, s3]
S += 0.2 * np.random.normal(size=S.shape)  # Add noise

S /= S.std(axis=0)  # Standardize data
# Mix data
A = np.array([[1, 1, 1], [0.5, 2, 1.0], [1.5, 1.0, 2.0]])  # Mixing matrix
X = np.dot(S, A.T)  # Generate observations

# Compute ICA
ica = FastICA(n_components=3)
S_ = ica.fit_transform(X)  # Reconstruct signals
A_ = ica.mixing_  # Get estimated mixing matrix

# We can `prove` that the ICA model applies by reverting the unmixing.
assert np.allclose(X, np.dot(S_, A_.T) + ica.mean_)

# For comparison, compute PCA
pca = PCA(n_components=3)
H = pca.fit_transform(X)  # Reconstruct signals based on orthogonal components

# #############################################################################
# Plot results

plt.figure()

models = [X, S, S_, H]
names = ['Observations (mixed signal)',
         'True Sources',
         'ICA recovered signals',
         'PCA recovered signals']
colors = ['red', 'steelblue', 'orange']

for ii, (model, name) in enumerate(zip(models, names), 1):
    plt.subplot(4, 1, ii)
    plt.title(name)
    for sig, color in zip(model.T, colors):
        plt.plot(sig, color=color)

plt.tight_layout()
plt.show()