Evaluación empírica del impacto de la inicialización de k-medias

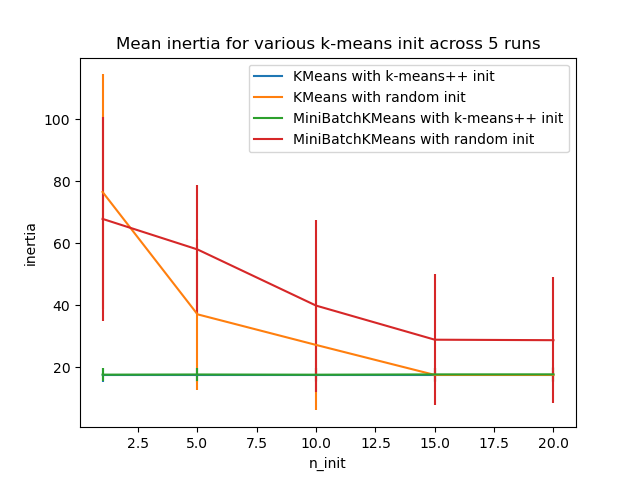
Evalua la capacidad de las estrategias de inicialización de k-medias para hacer que la convergencia del algoritmo sea robusta, medida por la desviación estándar relativa de la inercia del agrupamiento (es decir, la suma de las distancias al cuadrado al centro del conglomerado más cercano).

El primer gráfico muestra la mejor inercia alcanzada para cada combinación del modelo (KMeans o MiniBatchKMeans) y el método init (init="random" o init="kmeans++") para valores crecientes del parámetro n_init que controla el número de inicializaciones.

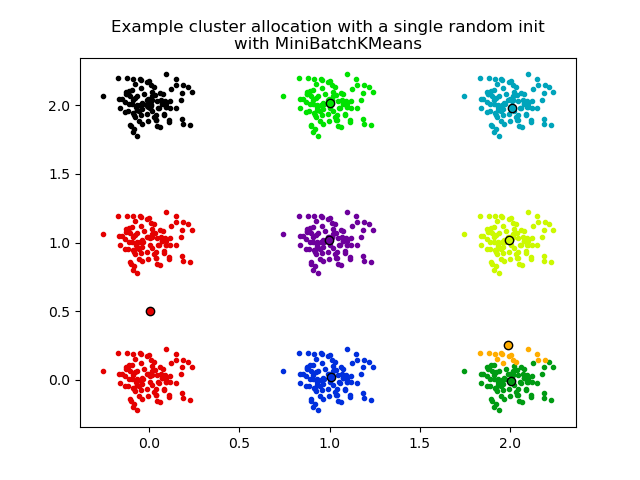
El segundo gráfico muestra una única ejecución del estimador MiniBatchKMeans utilizando un init="random" y n_init=1. Esta ejecución conduce a una mala convergencia (óptimo local) con los centros estimados atrapados entre los conglomerados verdaderos.

El conjunto de datos utilizado para la evaluación es una cuadrícula 2D de conglomerados Gaussianos isotrópicos ampliamente espaciados.

• 
• 

Out:

Evaluation of KMeans with k-means++ init
Evaluation of KMeans with random init
Evaluation of MiniBatchKMeans with k-means++ init
Evaluation of MiniBatchKMeans with random init

print(__doc__)

# Author: Olivier Grisel <olivier.grisel@ensta.org>
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm

from sklearn.utils import shuffle
from sklearn.utils import check_random_state
from sklearn.cluster import MiniBatchKMeans
from sklearn.cluster import KMeans

random_state = np.random.RandomState(0)

# Number of run (with randomly generated dataset) for each strategy so as
# to be able to compute an estimate of the standard deviation
n_runs = 5

# k-means models can do several random inits so as to be able to trade
# CPU time for convergence robustness
n_init_range = np.array([1, 5, 10, 15, 20])

# Datasets generation parameters
n_samples_per_center = 100
grid_size = 3
scale = 0.1
n_clusters = grid_size ** 2


def make_data(random_state, n_samples_per_center, grid_size, scale):
    random_state = check_random_state(random_state)
    centers = np.array([[i, j]
                        for i in range(grid_size)
                        for j in range(grid_size)])
    n_clusters_true, n_features = centers.shape

    noise = random_state.normal(
        scale=scale, size=(n_samples_per_center, centers.shape[1]))

    X = np.concatenate([c + noise for c in centers])
    y = np.concatenate([[i] * n_samples_per_center
                        for i in range(n_clusters_true)])
    return shuffle(X, y, random_state=random_state)

# Part 1: Quantitative evaluation of various init methods

plt.figure()
plots = []
legends = []

cases = [
    (KMeans, 'k-means++', {}),
    (KMeans, 'random', {}),
    (MiniBatchKMeans, 'k-means++', {'max_no_improvement': 3}),
    (MiniBatchKMeans, 'random', {'max_no_improvement': 3, 'init_size': 500}),
]

for factory, init, params in cases:
    print("Evaluation of %s with %s init" % (factory.__name__, init))
    inertia = np.empty((len(n_init_range), n_runs))

    for run_id in range(n_runs):
        X, y = make_data(run_id, n_samples_per_center, grid_size, scale)
        for i, n_init in enumerate(n_init_range):
            km = factory(n_clusters=n_clusters, init=init, random_state=run_id,
                         n_init=n_init, **params).fit(X)
            inertia[i, run_id] = km.inertia_
    p = plt.errorbar(n_init_range, inertia.mean(axis=1), inertia.std(axis=1))
    plots.append(p[0])
    legends.append("%s with %s init" % (factory.__name__, init))

plt.xlabel('n_init')
plt.ylabel('inertia')
plt.legend(plots, legends)
plt.title("Mean inertia for various k-means init across %d runs" % n_runs)

# Part 2: Qualitative visual inspection of the convergence

X, y = make_data(random_state, n_samples_per_center, grid_size, scale)
km = MiniBatchKMeans(n_clusters=n_clusters, init='random', n_init=1,
                     random_state=random_state).fit(X)

plt.figure()
for k in range(n_clusters):
    my_members = km.labels_ == k
    color = cm.nipy_spectral(float(k) / n_clusters, 1)
    plt.plot(X[my_members, 0], X[my_members, 1], 'o', marker='.', c=color)
    cluster_center = km.cluster_centers_[k]
    plt.plot(cluster_center[0], cluster_center[1], 'o',
             markerfacecolor=color, markeredgecolor='k', markersize=6)
    plt.title("Example cluster allocation with a single random init\n"
              "with MiniBatchKMeans")

plt.show()