2.4. Biclustering¶

El biclustering puede realizarse con el módulo sklearn.cluster.bicluster. Los algoritmos de biclustering agrupan simultáneamente filas y columnas de una matriz de datos. Estos clusters de filas y columnas se conocen como biclusters. Cada uno determina una submatriz de la matriz de datos original con algunas propiedades deseadas.

Por ejemplo, dada una matriz de forma (10, 10), un bicluster posible con tres filas y dos columnas induce un submatriz de la forma (3, 2):

>>>>>> import numpy as np
>>> data = np.arange(100).reshape(10, 10)
>>> rows = np.array([0, 2, 3])[:, np.newaxis]
>>> columns = np.array([1, 2])
>>> data[rows, columns]
array([[ 1,  2],
       [21, 22],
       [31, 32]])

Para fines de visualización, dado un bicluster, las filas y columnas de la matriz de datos pueden ser reorganizadas para hacer el bicluster contiguo.

Los algoritmos difieren en cómo se definen los biclusters. Algunos de los tipos comunes incluyen:

valores constantes, filas constantes o columnas constantes
valores inusualmente altos o bajos
submatrices con baja varianza
filas o columnas correlacionadas

Los algoritmos también difieren en la forma de asignar filas y columnas a los biclusters, lo que da lugar a diferentes estructuras de bicluster. Las estructuras de bloque diagonal o de tablero de ajedrez se producen cuando las filas y las columnas se dividen en particiones.

Si cada fila y cada columna pertenecen exactamente a un biclúster, el reordenamiento de las filas y columnas de la matriz de datos revela los biclústeres en la diagonal. He aquí un ejemplo de esta estructura en la que los biclusters tienen valores medios más altos que las demás filas y columnas:

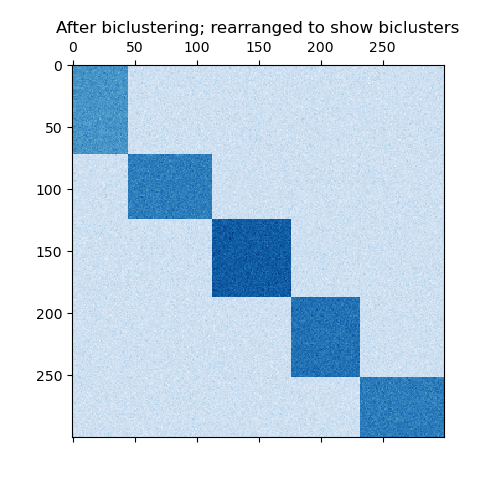
../_images/sphx_glr_plot_spectral_coclustering_003.png — Un ejemplo de biclusters formado por particionado de filas y columnas.¶

En el caso del tablero de ajedrez, cada fila pertenece a todos los grupos de columnas y cada columna pertenece a todos los grupos de filas. He aquí un ejemplo de esta estructura en la que la varianza de los valores dentro de cada bicluster es pequeña:

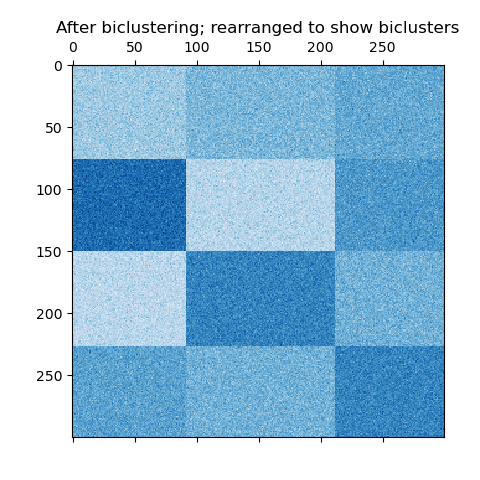
../_images/sphx_glr_plot_spectral_biclustering_003.png — Un ejemplo de biclusters de tablero de ajedrez.¶

Después de ajustar un modelo, la pertenencia a los clusters de filas y columnas se puede encontrar en los atributos rows_ y columns_. El atributo rows_[i] es un vector binario con entradas no nulas que corresponden a las filas que pertenecen al bicluster i. Del mismo modo, columns_[i] indica qué columnas pertenecen al bicluster i.

Algunos modelos también tienen atributos row_labels_ y column_labels_. Estos modelos particionan las filas y columnas, como en las estructuras de bicluster del bloque diagonal y del tablero de ajedrez.

Nota

El biclustering tiene muchos otros nombres en diferentes campos, como co-clustering, clustering de dos modos, clustering de dos vías, clustering de bloques, clustering de dos vías acoplado, etc. Los nombres de algunos algoritmos, como el algoritmo de Co-Clustering Espectral, reflejan estos nombres alternativos.

2.4.1. Co-Clustering espectral¶

El algoritmo SpectralCoclustering encuentra biclusters con valores más altos que los de las otras filas y columnas correspondientes. Cada fila y cada columna pertenecen exactamente a un biclúster, por lo que la reorganización de las filas y columnas para que las particiones sean contiguas revela estos valores altos a lo largo de la diagonal:

Nota

El algoritmo trata la matriz de datos de entrada como un grafo bipartito: las filas y columnas de la matriz corresponden a los dos conjuntos de vértices, y cada entrada corresponde a una arista entre una fila y una columna. El algoritmo aproxima el corte normalizado de este grafo para encontrar subgrafos pesados.

2.4.1.1. Formulación matemática¶

Una solución aproximada al corte óptimo normalizado puede encontrarse a través de la descomposición generalizada de valores propios del laplaciano del grafo. Normalmente, esto significaría trabajar directamente con la matriz laplaciana. Si la matriz de datos original $A$ tiene forma $m \times n$ , la matriz laplaciana del grafo bipartito correspondiente tiene forma $(m + n) \times (m + n)$ . Sin embargo, en este caso es posible trabajar directamente con $A$ , que es más pequeña y eficiente.

La matriz de entrada $A$ está preprocesada como sigue:

A_{n} = R^{- 1 / 2} A C^{- 1 / 2}

Donde $R$ es la matriz diagonal con la entrada $i$ igual a $\sum_{j} A_{i j}$ y $C$ es la matriz diagonal con la entrada $j$ igual a $\sum_{i} A_{i j}$ .

La descomposición del valor singular, $A_{n} = U Σ V^{⊤}$ , proporciona las particiones de las filas y columnas de $A$ . Un subconjunto de los vectores singulares de la izquierda da las particiones de las filas, y un subconjunto de los vectores singulares de la derecha da las particiones de las columnas.

Los vectores singulares $ℓ = ⌈ \log_{2} k ⌉$ , empezando por el segundo, proporcionan la información de partición deseada. Se utilizan para formar la matriz $Z$ :

\begin{array}{r} Z = [\begin{array}{c} R^{- 1 / 2} U \\ C^{- 1 / 2} V \end{array}] \end{array}

donde las columnas de $U$ son $u_{2}, \dots, u_{ℓ + 1}$ , y similarmente para $V$ .

A continuación, las filas de $Z$ se agrupan utilizando k-means. Las primeras etiquetas n_rows proporcionan la partición de las filas, y las restantes etiquetas n_columns proporcionan la partición de las columnas.

Ejemplos:

Una demostración del algoritmo de Co-Clustering Espectral: Un ejemplo simple que muestra cómo generar una matriz de datos con biclusters y aplicar este método a ella.
Biclustering de documentos con el algoritmo Co-clustering Espectral: Un ejemplo de búsqueda de biclusters en el conjunto de datos de veinte grupos de comunicación.

Referencias:

Dhillon, Inderjit S, 2001. Co-clustering documents and words using bipartite spectral graph partitioning.

2.4.2. Biclustering espectral¶

El algoritmo SpectralBiclustering supone que la matriz de datos de entrada tiene una estructura de tablero de ajedrez oculto. Las filas y las columnas de una matriz con esta estructura pueden dividirse de forma que las entradas de cualquier bicluster en el producto cartesiano de los clusters de filas y los clusters de columnas sean aproximadamente constantes. Por ejemplo, si hay dos particiones de filas y tres de columnas, cada fila pertenecerá a tres biclústeres y cada columna pertenecerá a dos biclústeres.

El algoritmo divide las filas y las columnas de una matriz de modo que la correspondiente matriz en forma de tablero de ajedrez con constantes de bloque proporciona una buena aproximación a la matriz original.

2.4.2.1. Formulación matemática¶

La matriz de entrada $A$ se normaliza primero para que el patrón de tablero de ajedrez sea más evidente. Hay tres métodos posibles:

Normalización independiente de filas y columnas, como en el Co-Clustering Espectral. Este método hace que las filas sumen una constante y las columnas sumen una constante diferente.
Bistocastizacion: normalización repetida de filas y columnas hasta la convergencia. Este método hace que tanto las filas como las columnas sumen la misma constante.
Normalización logarítmica: se calcula el logaritmo de la matriz de datos: $L = \log A$ . A continuación, se calcula la media de las columnas $o v e r l i n e L_{i \cdot}, l a m e d i a d e l a s f i l a s : m a t h :$ overline{L_{cdot j}}, y la media global $\overset{―}{L_{c d o t \cdot}} d e : m a t h :$ . La matriz final se calcula según la fórmula

K_{i j} = L_{i j} - \overset{―}{L_{i \cdot}} - \overset{―}{L_{\cdot j}} + \overset{―}{L_{\cdot \cdot}}

Después de la normalización, se calculan los primeros vectores singulares, al igual que en el algoritmo de coagrupación espectral.

Si se utilizó la normalización logarítmica, todos los vectores singulares son significativos. Sin embargo, si se utilizó la normalización independiente o la bistocastizacion, los primeros vectores singulares, $u_{1}$ y $v_{1}$ . se descartan. A partir de ahora, los «primeros» vectores singulares se refieren a $u_{2} \dots u_{p + 1}$ y $v_{2} \dots v_{p + 1}$ excepto en el caso de la normalización logarítmica.

Dados estos vectores singulares, se clasifican en función de cuál de ellos puede ser mejor aproximado por un vector a trozos. Las aproximaciones de cada vector se encuentran utilizando k-means unidimensional y se califican utilizando la distancia euclidiana. Se selecciona un subconjunto del mejor vector singular izquierdo y derecho. A continuación, los datos se proyectan a este mejor subconjunto de vectores singulares y se agrupan.

Por ejemplo, si se calcularon los vectores singulares $p$ , se encuentran los mejores $q$ como se ha descrito, donde $q < p$ . Sea $U$ la matriz con las columnas de los vectores singulares $q$ mejores de la izquierda, y de forma similar $V$ para la derecha. Para dividir las filas, las filas de $A$ se proyectan a un espacio dimensional $q$ : $A * V$ . Tratando las filas $m$ de esta matriz $m \times q$ como muestras y agrupando mediante k-means se obtienen las etiquetas de las filas. Del mismo modo, la proyección de las columnas a $A^{⊤} * U$ y la agrupación de esta matriz $n \times q$ produce las etiquetas de las columnas.

Ejemplos:

Una demostración del algoritmo Biclustering Espectral: un ejemplo simple que muestra cómo generar una matriz de tablero de ajedrez y bicluster.

Referencias:

Kluger, Yuval, et. al., 2003. Spectral biclustering of microarray data: coclustering genes and conditions.

2.4.3. Evaluación de Biclustering¶

Hay dos formas de evaluar un resultado de biclustering: interna y externa. Las medidas internas, como la estabilidad de los clusters, se basan únicamente en los datos y en el propio resultado. Actualmente no hay medidas internas de bicluster en scikit-learn. Las medidas externas se refieren a una fuente de información externa, como la solución verdadera. Cuando se trabaja con datos reales, la solución verdadera suele ser desconocida, pero el biclustering de datos artificiales puede ser útil para evaluar algoritmos precisamente porque la solución verdadera es conocida.

Para comparar un conjunto de biclusters encontrados con el conjunto de biclusters verdaderos, se necesitan dos medidas de similitud: una medida de similitud para los biclusters individuales, y una forma de combinar estas similitudes individuales en una puntuación global.

Para comparar biclusters individuales, se han utilizado varias medidas. Por ahora, sólo se aplica el índice de Jaccard:

J (A, B) = \frac{| A \cap B |}{| A | + | B | - | A \cap B |}

donde $A$ y $B$ son biclusters, $| A \cap B |$ es el número de elementos en su intersección. El índice de la tarjeta de crédito alcanza su mínimo de 0 cuando los biclusters para no solaparse en absoluto y su máximo de 1 cuando son idénticos.

Se han desarrollado varios métodos para comparar dos conjuntos de biclusters. Por ahora, solo consensus_score (Hochreiter et. al., 2010) está disponible:

Calcula las similitudes de bicluster para pares de biclusters, una en cada conjunto, utilizando el índice de Jaccard o una medida similar.
Asigna biclusters de un conjunto a otro de una manera una-a otra para maximizar la suma de sus similitudes. Este paso se realiza utilizando el algoritmo húngaro.
La suma final de similitudes se divide por el tamaño del conjunto más grande.

La puntuación mínima de consenso, 0, se produce cuando todos los pares de biclusters son totalmente disímiles. La puntuación máxima, 1, se produce cuando ambos conjuntos son idénticos.

Referencias:

Hochreiter, Bodenhofer, et. al., 2010. FABIA: factor analysis for bicluster acquisition.