Graficar los coeficientes Ridge en función de la regularización L2

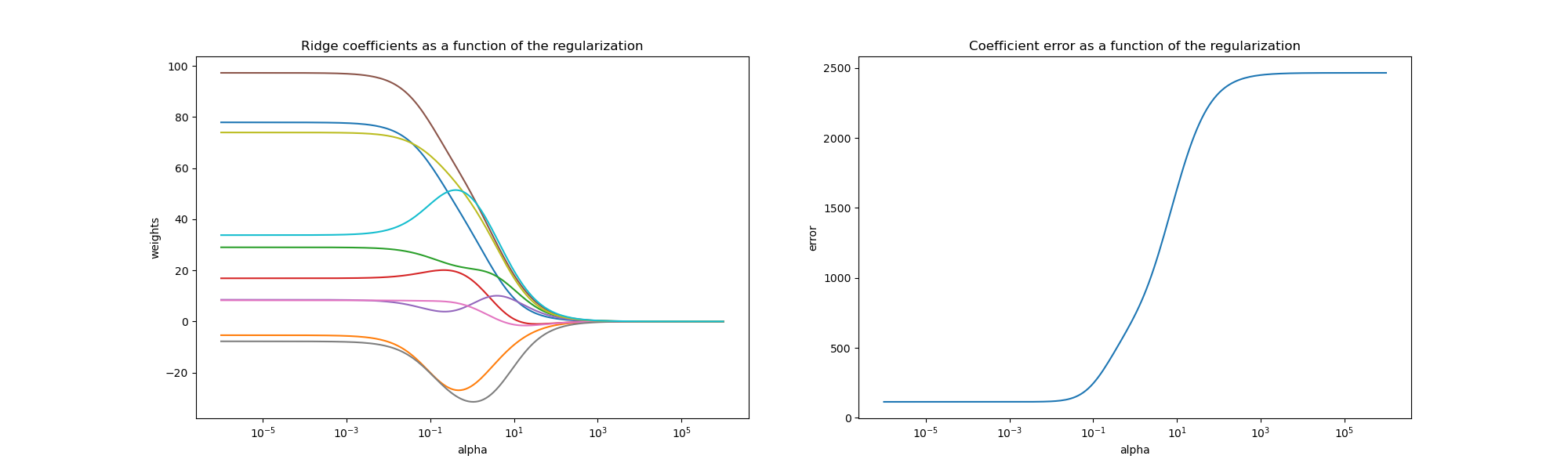
Regresión Ridge es el estimador utilizado en este ejemplo. Cada color en el gráfico de la izquierda representa una dimensión diferente del vector de coeficientes, y esto se muestra como una función del parámetro de regularización. El gráfico de la derecha muestra la exactitud de la solución. Este ejemplo ilustra cómo se encuentra una solución bien definida mediante la regresión Ridge y cómo la regularización afecta a los coeficientes y sus valores. El gráfico de la derecha muestra cómo cambia la diferencia de los coeficientes del estimador en función de la regularización.

En este ejemplo, la variable dependiente Y se establece como una función de las características de entrada: y = X*w + c. El vector de coeficientes w se extrae aleatoriamente de una distribución normal, mientras que el término de sesgo c se establece como una constante.

A medida que alfa tiende a cero, los coeficientes encontrados por la regresión de Ridge se estabilizan hacia el vector w muestreado aleatoriamente. Para alfa grande (regularización fuerte) los coeficientes son más pequeños (eventualmente convergen a 0) lo que lleva a una solución más simple y sesgada. Estas dependencias pueden observarse en el gráfico de la izquierda.

El gráfico de la derecha muestra el error cuadrático medio entre los coeficientes encontrados por el modelo y el vector w elegido. Los modelos menos regularizados recuperan los coeficientes exactos (el error es igual a 0), los modelos más regularizados aumentan el error.

Ten en cuenta que en este ejemplo los datos no tienen ruido, por lo que es posible extraer los coeficientes exactos.

# Author: Kornel Kielczewski -- <kornel.k@plusnet.pl>

print(__doc__)

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_regression
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error

clf = Ridge()

X, y, w = make_regression(n_samples=10, n_features=10, coef=True,
                          random_state=1, bias=3.5)

coefs = []
errors = []

alphas = np.logspace(-6, 6, 200)

# Train the model with different regularisation strengths
for a in alphas:
    clf.set_params(alpha=a)
    clf.fit(X, y)
    coefs.append(clf.coef_)
    errors.append(mean_squared_error(clf.coef_, w))

# Display results
plt.figure(figsize=(20, 6))

plt.subplot(121)
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')

plt.subplot(122)
ax = plt.gca()
ax.plot(alphas, errors)
ax.set_xscale('log')
plt.xlabel('alpha')
plt.ylabel('error')
plt.title('Coefficient error as a function of the regularization')
plt.axis('tight')

plt.show()