Varianza de mínimos cuadrados ordinarios y regresión Ridge

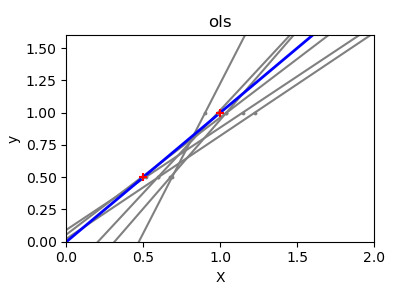
Debido a los pocos puntos de cada dimensión y a la línea recta que utiliza la regresión lineal para seguir estos puntos lo mejor posible, el ruido en las observaciones provocará una gran variación, como se muestra en el primer gráfico. La pendiente de cada línea puede variar bastante para cada predicción debido al ruido inducido en las observaciones.

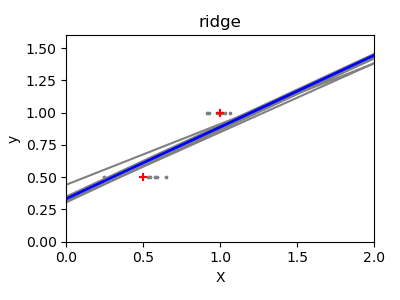
La regresión Ridge consiste básicamente en minimizar una versión penalizada de la función de mínimos cuadrados. La penalización reduce el valor de los coeficientes de regresión. A pesar de los pocos puntos de datos en cada dimensión, la pendiente de la predicción es mucho más estable y la varianza de la propia línea se reduce considerablemente, en comparación con la de la regresión lineal estándar

• 
• 

print(__doc__)


# Code source: Gaël Varoquaux
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause


import numpy as np
import matplotlib.pyplot as plt

from sklearn import linear_model

X_train = np.c_[.5, 1].T
y_train = [.5, 1]
X_test = np.c_[0, 2].T

np.random.seed(0)

classifiers = dict(ols=linear_model.LinearRegression(),
                   ridge=linear_model.Ridge(alpha=.1))

for name, clf in classifiers.items():
    fig, ax = plt.subplots(figsize=(4, 3))

    for _ in range(6):
        this_X = .1 * np.random.normal(size=(2, 1)) + X_train
        clf.fit(this_X, y_train)

        ax.plot(X_test, clf.predict(X_test), color='gray')
        ax.scatter(this_X, y_train, s=3, c='gray', marker='o', zorder=10)

    clf.fit(X_train, y_train)
    ax.plot(X_test, clf.predict(X_test), linewidth=2, color='blue')
    ax.scatter(X_train, y_train, s=30, c='red', marker='+', zorder=10)

    ax.set_title(name)
    ax.set_xlim(0, 2)
    ax.set_ylim((0, 1.6))
    ax.set_xlabel('X')
    ax.set_ylabel('y')

    fig.tight_layout()

plt.show()