Agrupamiento espectral para la segmentación de imágenes

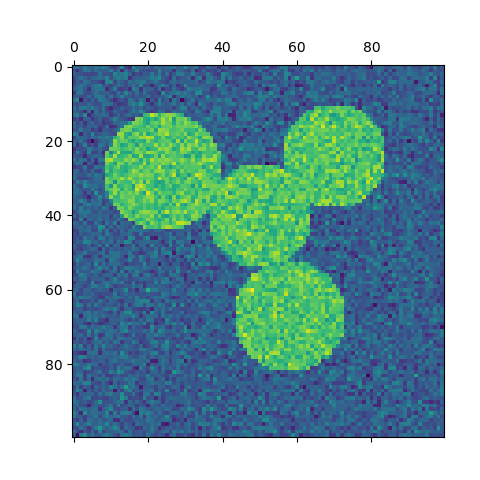
En este ejemplo, se genera una imagen con círculos conectados y se utiliza el agrupamiento espectral para separar los círculos.

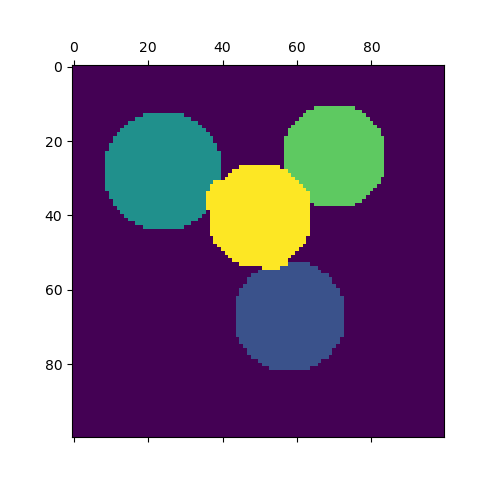
En estos casos, el enfoque Análisis espectral de conglomerados resuelve el problema conocido como “cortes de grafos normalizados”: la imagen se ve como un grafo de vóxeles conectados, y el algoritmo de agrupamiento espectral consiste en elegir cortes de grafos que definen regiones mientras se minimiza la relación entre el gradiente a lo largo del corte y el volumen de la región.

A medida que el algoritmo intenta equilibrar el volumen (es decir, equilibrar los tamaños de las regiones), si tomamos círculos con tamaños diferentes, la segmentación falla.

Además, como no hay información útil en la intensidad de la imagen, ni en su gradiente, elegimos realizar el agrupamiento espectral en un grafo que sólo está débilmente informado por el gradiente. Esto se aproxima a la realización de una partición de Voronoi del grafo.

Además, utilizamos la máscara de los objetos para restringir el grafo al contorno de los objetos. En este ejemplo, nos interesa separar los objetos unos de otros, y no del fondo.

• 
• 
• 
• 

print(__doc__)

# Authors:  Emmanuelle Gouillart <emmanuelle.gouillart@normalesup.org>
#           Gael Varoquaux <gael.varoquaux@normalesup.org>
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.feature_extraction import image
from sklearn.cluster import spectral_clustering

l = 100
x, y = np.indices((l, l))

center1 = (28, 24)
center2 = (40, 50)
center3 = (67, 58)
center4 = (24, 70)

radius1, radius2, radius3, radius4 = 16, 14, 15, 14

circle1 = (x - center1[0]) ** 2 + (y - center1[1]) ** 2 < radius1 ** 2
circle2 = (x - center2[0]) ** 2 + (y - center2[1]) ** 2 < radius2 ** 2
circle3 = (x - center3[0]) ** 2 + (y - center3[1]) ** 2 < radius3 ** 2
circle4 = (x - center4[0]) ** 2 + (y - center4[1]) ** 2 < radius4 ** 2

# #############################################################################
# 4 circles
img = circle1 + circle2 + circle3 + circle4

# We use a mask that limits to the foreground: the problem that we are
# interested in here is not separating the objects from the background,
# but separating them one from the other.
mask = img.astype(bool)

img = img.astype(float)
img += 1 + 0.2 * np.random.randn(*img.shape)

# Convert the image into a graph with the value of the gradient on the
# edges.
graph = image.img_to_graph(img, mask=mask)

# Take a decreasing function of the gradient: we take it weakly
# dependent from the gradient the segmentation is close to a voronoi
graph.data = np.exp(-graph.data / graph.data.std())

# Force the solver to be arpack, since amg is numerically
# unstable on this example
labels = spectral_clustering(graph, n_clusters=4, eigen_solver='arpack')
label_im = np.full(mask.shape, -1.)
label_im[mask] = labels

plt.matshow(img)
plt.matshow(label_im)

# #############################################################################
# 2 circles
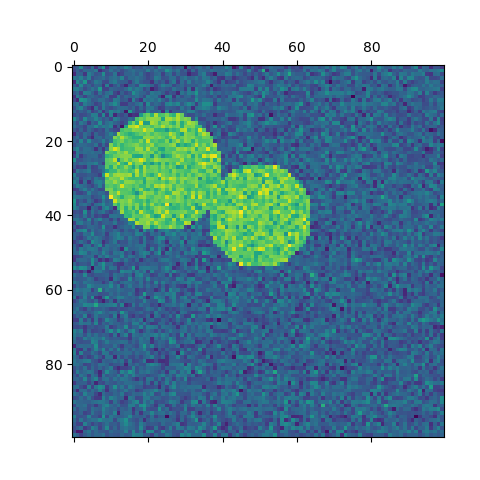
img = circle1 + circle2
mask = img.astype(bool)
img = img.astype(float)

img += 1 + 0.2 * np.random.randn(*img.shape)

graph = image.img_to_graph(img, mask=mask)
graph.data = np.exp(-graph.data / graph.data.std())

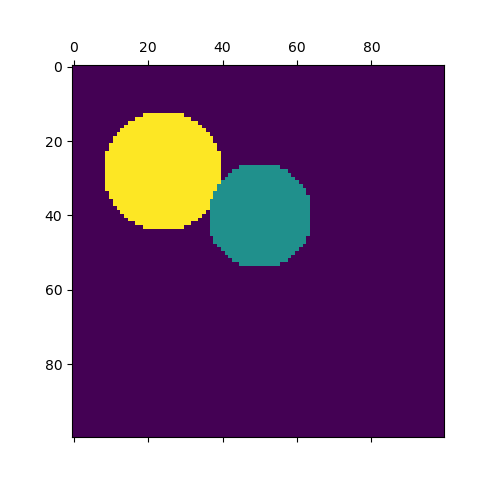
labels = spectral_clustering(graph, n_clusters=2, eigen_solver='arpack')
label_im = np.full(mask.shape, -1.)
label_im[mask] = labels

plt.matshow(img)
plt.matshow(label_im)

plt.show()