Demostración (demo) del agrupamiento por K-Medias en los datos de dígitos escritos a mano

En este ejemplo comparamos las distintas estrategias de inicialización para K-medias en términos de tiempo de ejecución y calidad de los resultados.

Como la verdad fundamental es conocida aquí, también aplicamos diferentes métricas de calidad de los conglomerados para juzgar la bondad de ajuste de las etiquetas de los conglomerados a la verdad fundamental.

Métricas de calidad del conglomerado evaluadas (consulta Evaluación del rendimiento del análisis de conglomerados (agrupamiento) para las definiciones y discusiones de las métricas):

Abreviatura	nombre completo
homo	homogeneity score (puntuación de homogeneidad)
compl	completeness score (puntuación de completitud)
v-meas	V measure (Medida V)
ARI	adjusted Rand index (índice de Rand ajustado)
AMI	adjusted mutual information (información mutua ajustada)
silhouette	silhouette coefficient (coeficiente de silueta)

print(__doc__)

Cargar el conjunto de datos

Empezaremos cargando el conjunto de datos digits. Este conjunto de datos contiene dígitos escritos a mano del 0 al 9. En el contexto del conglomerado, se quiere agrupar las imágenes de manera que los dígitos escritos a mano en la imagen sean los mismos.

import numpy as np
from sklearn.datasets import load_digits

data, labels = load_digits(return_X_y=True)
(n_samples, n_features), n_digits = data.shape, np.unique(labels).size

print(
    f"# digits: {n_digits}; # samples: {n_samples}; # features {n_features}"
)

Out:

# digits: 10; # samples: 1797; # features 64

Define nuestro punto de referencia para la evaluación

Primero veremos nuestro punto de referencia de evaluación. Durante este punto de referencia, pretendemos comparar diferentes métodos de inicialización para KMeans. Nuestro punto de referencia será:

• crea un pipeline que escalará los datos usando un StandardScaler;

• entrena y cronometra el ajuste del pipeline;

• mide el rendimiento del agrupamiento obtenido a través de diferentes métricas.

from time import time
from sklearn import metrics
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler


def bench_k_means(kmeans, name, data, labels):
    """Benchmark to evaluate the KMeans initialization methods.

    Parameters
    ----------
    kmeans : KMeans instance
        A :class:`~sklearn.cluster.KMeans` instance with the initialization
        already set.
    name : str
        Name given to the strategy. It will be used to show the results in a
        table.
    data : ndarray of shape (n_samples, n_features)
        The data to cluster.
    labels : ndarray of shape (n_samples,)
        The labels used to compute the clustering metrics which requires some
        supervision.
    """
    t0 = time()
    estimator = make_pipeline(StandardScaler(), kmeans).fit(data)
    fit_time = time() - t0
    results = [name, fit_time, estimator[-1].inertia_]

    # Define the metrics which require only the true labels and estimator
    # labels
    clustering_metrics = [
        metrics.homogeneity_score,
        metrics.completeness_score,
        metrics.v_measure_score,
        metrics.adjusted_rand_score,
        metrics.adjusted_mutual_info_score,
    ]
    results += [m(labels, estimator[-1].labels_) for m in clustering_metrics]

    # The silhouette score requires the full dataset
    results += [
        metrics.silhouette_score(data, estimator[-1].labels_,
                                 metric="euclidean", sample_size=300,)
    ]

    # Show the results
    formatter_result = ("{:9s}\t{:.3f}s\t{:.0f}\t{:.3f}\t{:.3f}"
                        "\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}")
    print(formatter_result.format(*results))

Ejecutar el punto de referencia

Compararemos tres enfoques:

• una inicialización utilizando kmeans++. Este método es estocástico y ejecutaremos la inicialización 4 veces;

• una inicialización aleatoria. Este método también es estocástico y ejecutaremos la inicialización 4 veces;

• una inicialización basada en una proyección PCA. De hecho, utilizaremos los componentes de PCA para inicializar KMeans. Este método es determinista y una sola inicialización es suficiente.

from sklearn.cluster import KMeans
from sklearn.decomposition import PCA

print(82 * '_')
print('init\t\ttime\tinertia\thomo\tcompl\tv-meas\tARI\tAMI\tsilhouette')

kmeans = KMeans(init="k-means++", n_clusters=n_digits, n_init=4,
                random_state=0)
bench_k_means(kmeans=kmeans, name="k-means++", data=data, labels=labels)

kmeans = KMeans(init="random", n_clusters=n_digits, n_init=4, random_state=0)
bench_k_means(kmeans=kmeans, name="random", data=data, labels=labels)

pca = PCA(n_components=n_digits).fit(data)
kmeans = KMeans(init=pca.components_, n_clusters=n_digits, n_init=1)
bench_k_means(kmeans=kmeans, name="PCA-based", data=data, labels=labels)

print(82 * '_')

Out:

__________________________________________________________________________________
init            time    inertia homo    compl   v-meas  ARI     AMI     silhouette
k-means++       0.780s  69662   0.680   0.719   0.699   0.570   0.695   0.173
random          0.404s  69707   0.675   0.716   0.694   0.560   0.691   0.188
PCA-based       0.194s  72686   0.636   0.658   0.647   0.521   0.643   0.144
__________________________________________________________________________________

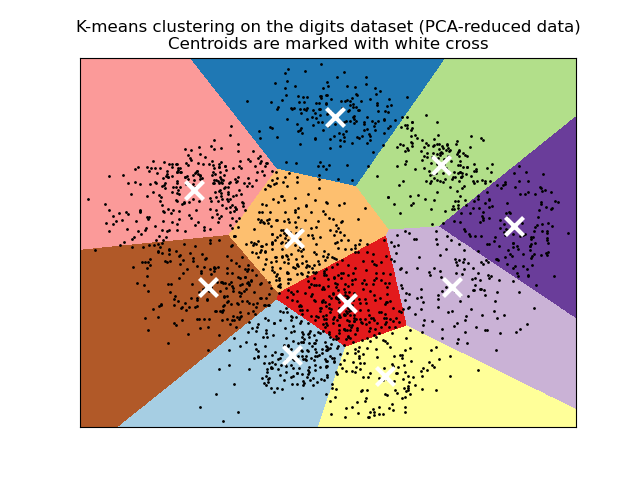
Visualiza los resultados de los datos reducidos por el PCA

PCA permite proyectar los datos desde el espacio original de 64 dimensiones a un espacio de menor dimensión. Posteriormente, podemos utilizar PCA para proyectar en un espacio de 2 dimensiones y graficar los datos y los conglomerados en este nuevo espacio.

import matplotlib.pyplot as plt

reduced_data = PCA(n_components=2).fit_transform(data)
kmeans = KMeans(init="k-means++", n_clusters=n_digits, n_init=4)
kmeans.fit(reduced_data)

# Step size of the mesh. Decrease to increase the quality of the VQ.
h = .02     # point in the mesh [x_min, x_max]x[y_min, y_max].

# Plot the decision boundary. For that, we will assign a color to each
x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1
y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

# Obtain labels for each point in mesh. Use last trained model.
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])

# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1)
plt.clf()
plt.imshow(Z, interpolation="nearest",
           extent=(xx.min(), xx.max(), yy.min(), yy.max()),
           cmap=plt.cm.Paired, aspect="auto", origin="lower")

plt.plot(reduced_data[:, 0], reduced_data[:, 1], 'k.', markersize=2)
# Plot the centroids as a white X
centroids = kmeans.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1], marker="x", s=169, linewidths=3,
            color="w", zorder=10)
plt.title("K-means clustering on the digits dataset (PCA-reduced data)\n"
          "Centroids are marked with white cross")
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()