Diferentes agrupamientos aglomerativos en una incrustación 2D de dígitos

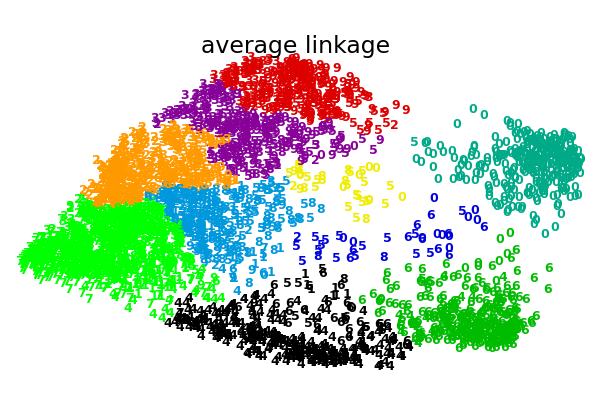
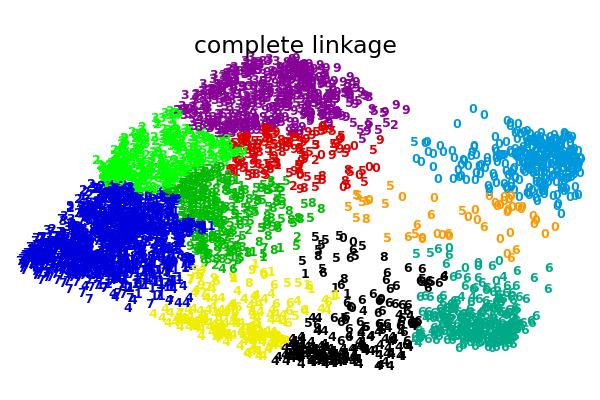
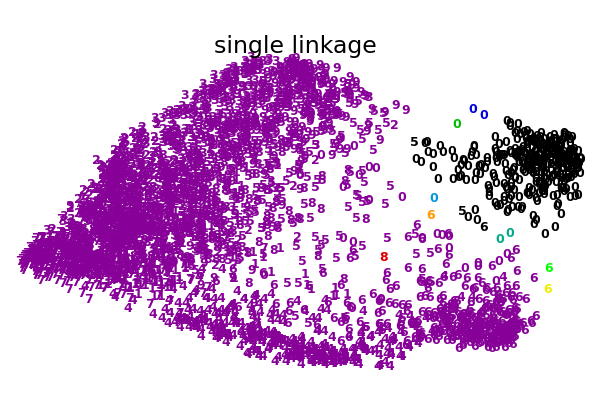
Una ilustración de varias opciones de enlazamiento para el agrupamiento aglomerativo en una incrustación 2D del conjunto de datos de dígitos.

El objetivo de este ejemplo es mostrar intuitivamente cómo se comportan las métricas, y no encontrar buenos conglomerados para los dígitos. Por eso el ejemplo funciona en una incrustación 2D.

Lo que este ejemplo nos muestra es el comportamiento «rico que se enriquece» del agrupamiento aglomerativo que tiende a crear tamaños de conglomerados desiguales. Este comportamiento es pronunciado para la estrategia de enlazamiento promedio, que termina con un par de conglomerados únicos, mientras que en el caso de la vinculación única obtenemos un único conglomerado central con todos los demás conglomerados extraídos de puntos de ruido alrededor de los bordes.

• 
• 
• 
• 

Out:

Computing embedding
Done.
ward :  0.38s
average :       0.31s
complete :      0.29s
single :        0.09s

# Authors: Gael Varoquaux
# License: BSD 3 clause (C) INRIA 2014

print(__doc__)
from time import time

import numpy as np
from scipy import ndimage
from matplotlib import pyplot as plt

from sklearn import manifold, datasets

X, y = datasets.load_digits(return_X_y=True)
n_samples, n_features = X.shape

np.random.seed(0)

def nudge_images(X, y):
    # Having a larger dataset shows more clearly the behavior of the
    # methods, but we multiply the size of the dataset only by 2, as the
    # cost of the hierarchical clustering methods are strongly
    # super-linear in n_samples
    shift = lambda x: ndimage.shift(x.reshape((8, 8)),
                                  .3 * np.random.normal(size=2),
                                  mode='constant',
                                  ).ravel()
    X = np.concatenate([X, np.apply_along_axis(shift, 1, X)])
    Y = np.concatenate([y, y], axis=0)
    return X, Y


X, y = nudge_images(X, y)


#----------------------------------------------------------------------
# Visualize the clustering
def plot_clustering(X_red, labels, title=None):
    x_min, x_max = np.min(X_red, axis=0), np.max(X_red, axis=0)
    X_red = (X_red - x_min) / (x_max - x_min)

    plt.figure(figsize=(6, 4))
    for i in range(X_red.shape[0]):
        plt.text(X_red[i, 0], X_red[i, 1], str(y[i]),
                 color=plt.cm.nipy_spectral(labels[i] / 10.),
                 fontdict={'weight': 'bold', 'size': 9})

    plt.xticks([])
    plt.yticks([])
    if title is not None:
        plt.title(title, size=17)
    plt.axis('off')
    plt.tight_layout(rect=[0, 0.03, 1, 0.95])

#----------------------------------------------------------------------
# 2D embedding of the digits dataset
print("Computing embedding")
X_red = manifold.SpectralEmbedding(n_components=2).fit_transform(X)
print("Done.")

from sklearn.cluster import AgglomerativeClustering

for linkage in ('ward', 'average', 'complete', 'single'):
    clustering = AgglomerativeClustering(linkage=linkage, n_clusters=10)
    t0 = time()
    clustering.fit(X_red)
    print("%s :\t%.2fs" % (linkage, time() - t0))

    plot_clustering(X_red, clustering.labels_, "%s linkage" % linkage)


plt.show()