Agrupamiento aglomerativo con diferentes métricas

Demuestra el efecto de diferentes métricas en el agrupamiento jerárquico.

El ejemplo está diseñado para mostrar el efecto de la elección de diferentes métricas. Se aplica a formas de onda, que pueden verse como vectores de alta dimensión. De hecho, la diferencia entre las métricas suele ser más pronunciada en la dimensión alta (en particular para la euclidiana y la cityblock).

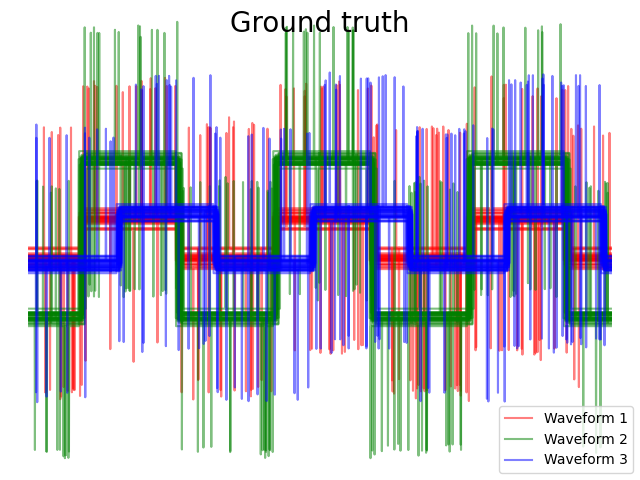
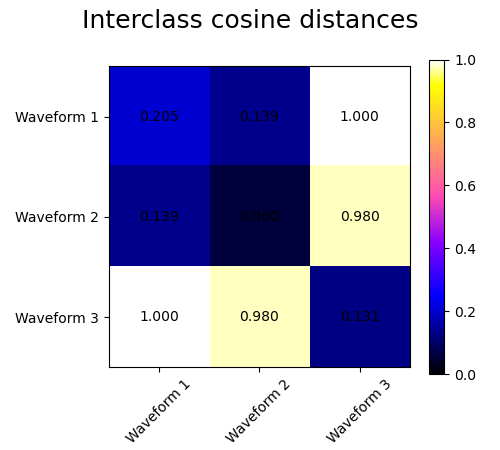
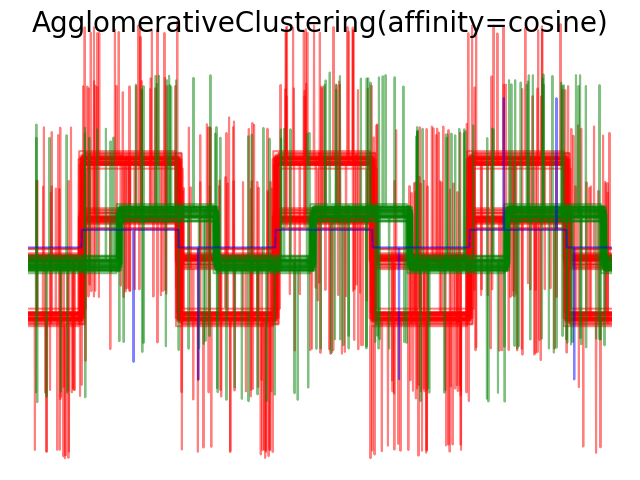
Generamos datos a partir de tres grupos de formas de onda. Dos de las formas de onda (forma de onda 1 y forma de onda 2) son proporcionales entre sí. La distancia coseno es invariante a un escalamiento de los datos, como resultado, no puede distinguir estas dos formas de onda. Por lo tanto, incluso sin ruido, el agrupamiento utilizando esta distancia no separará las formas de onda 1 y 2.

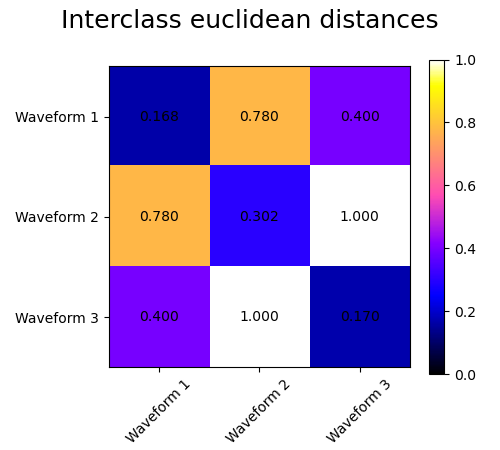
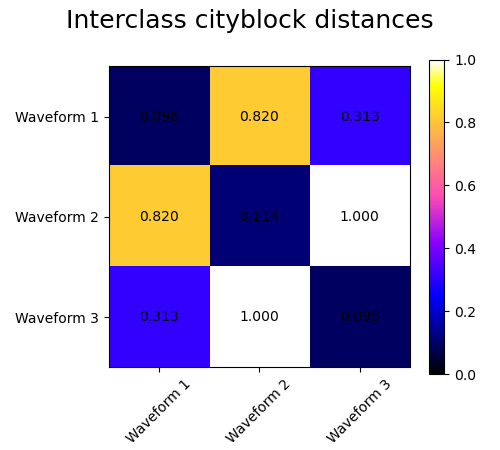
Añadimos ruido de observación a estas formas de onda. Generamos un ruido muy disperso: sólo el 6% de los puntos temporales contienen ruido. Como resultado, la norma l1 de este ruido (es decir, la distancia «cityblock») es mucho menor que su norma l2 (distancia «euclidiana»). Esto puede verse en las matrices de distancia entre clases: los valores de la diagonal, que caracterizan la dispersión de la clase, son mucho mayores para la distancia Euclidina que para la distancia cityblock.

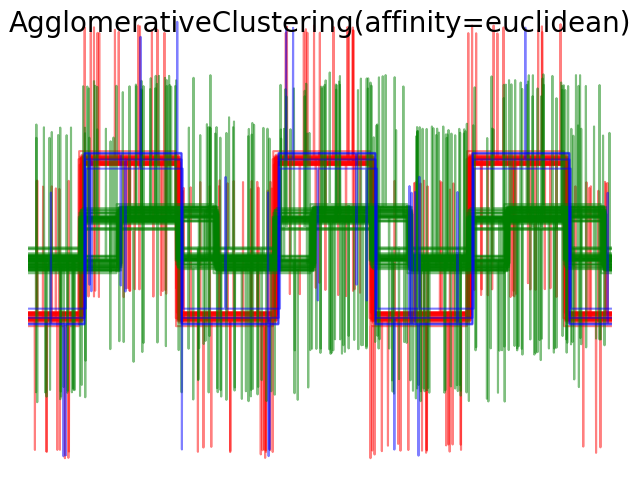
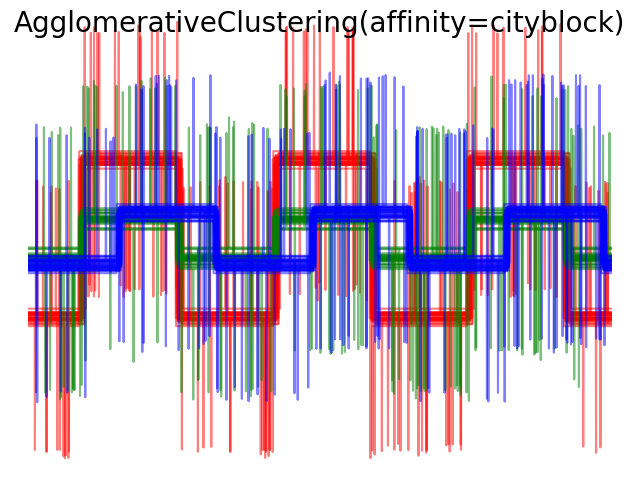
Cuando aplicamos el agrupamiento a los datos, comprobamos que la agrupación refleja lo que había en las matrices de distancia. En efecto, para la distancia Euclidiana, las clases están mal separadas debido al ruido y, por tanto, el agrupamiento no separa las formas de onda. Para la distancia cityblock, la separación es buena y se recuperan las clases de forma de onda. Por último, la distancia coseno no separa en absoluto las formas de onda 1 y 2, por lo que el agrupamiento las coloca en el mismo conglomerado.

• 
• 
• 
• 
• 
• 
• 

# Author: Gael Varoquaux
# License: BSD 3-Clause or CC-0

import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import AgglomerativeClustering
from sklearn.metrics import pairwise_distances

np.random.seed(0)

# Generate waveform data
n_features = 2000
t = np.pi * np.linspace(0, 1, n_features)


def sqr(x):
    return np.sign(np.cos(x))

X = list()
y = list()
for i, (phi, a) in enumerate([(.5, .15), (.5, .6), (.3, .2)]):
    for _ in range(30):
        phase_noise = .01 * np.random.normal()
        amplitude_noise = .04 * np.random.normal()
        additional_noise = 1 - 2 * np.random.rand(n_features)
        # Make the noise sparse
        additional_noise[np.abs(additional_noise) < .997] = 0

        X.append(12 * ((a + amplitude_noise)
                 * (sqr(6 * (t + phi + phase_noise)))
                 + additional_noise))
        y.append(i)

X = np.array(X)
y = np.array(y)

n_clusters = 3

labels = ('Waveform 1', 'Waveform 2', 'Waveform 3')

# Plot the ground-truth labelling
plt.figure()
plt.axes([0, 0, 1, 1])
for l, c, n in zip(range(n_clusters), 'rgb',
                   labels):
    lines = plt.plot(X[y == l].T, c=c, alpha=.5)
    lines[0].set_label(n)

plt.legend(loc='best')

plt.axis('tight')
plt.axis('off')
plt.suptitle("Ground truth", size=20)


# Plot the distances
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
    avg_dist = np.zeros((n_clusters, n_clusters))
    plt.figure(figsize=(5, 4.5))
    for i in range(n_clusters):
        for j in range(n_clusters):
            avg_dist[i, j] = pairwise_distances(X[y == i], X[y == j],
                                                metric=metric).mean()
    avg_dist /= avg_dist.max()
    for i in range(n_clusters):
        for j in range(n_clusters):
            plt.text(i, j, '%5.3f' % avg_dist[i, j],
                     verticalalignment='center',
                     horizontalalignment='center')

    plt.imshow(avg_dist, interpolation='nearest', cmap=plt.cm.gnuplot2,
               vmin=0)
    plt.xticks(range(n_clusters), labels, rotation=45)
    plt.yticks(range(n_clusters), labels)
    plt.colorbar()
    plt.suptitle("Interclass %s distances" % metric, size=18)
    plt.tight_layout()


# Plot clustering results
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
    model = AgglomerativeClustering(n_clusters=n_clusters,
                                    linkage="average", affinity=metric)
    model.fit(X)
    plt.figure()
    plt.axes([0, 0, 1, 1])
    for l, c in zip(np.arange(model.n_clusters), 'rgbk'):
        plt.plot(X[model.labels_ == l].T, c=c, alpha=.5)
    plt.axis('tight')
    plt.axis('off')
    plt.suptitle("AgglomerativeClustering(affinity=%s)" % metric, size=20)


plt.show()