Efecto de la variación del umbral de autoentrenamiento

Este ejemplo ilustra el efecto de un umbral variable en el autoentrenamiento. Se carga el conjunto de datos breast_cancer y se eliminan las etiquetas de forma que sólo 50 de 569 muestras tienen etiquetas. En este conjunto de datos se ajusta un SelfTrainingClassifier con umbrales variables.

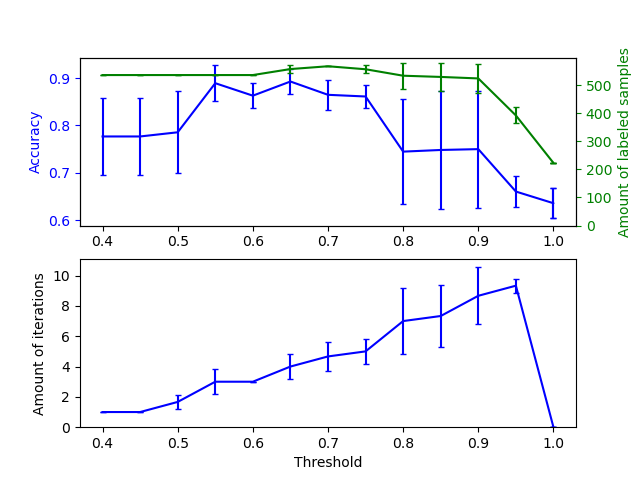
El gráfico superior muestra la cantidad de muestras etiquetadas que tiene el clasificador al final del ajuste, y la precisión del clasificador. El gráfico inferior muestra la última iteración en la que se etiquetó una muestra. Todos los valores están validados de forma cruzada con 3 pliegues (folds).

En los umbrales bajos (en [0.4, 0.5]), el clasificador aprende de las muestras que fueron etiquetadas con una confianza baja. Es probable que estas muestras de baja confianza tengan etiquetas predichas incorrectas y, como resultado, el ajuste sobre estas etiquetas incorrectas produce una exactitud deficiente. Ten en cuenta que el clasificador etiqueta casi todas las muestras y que sólo necesita una iteración.

Para umbrales muy altos (en [0.9, 1)) observamos que el clasificador no aumenta su conjunto de datos (la cantidad de muestras autoetiquetadas es 0). Como resultado, la exactitud alcanzada con un umbral de 0.9999 es la misma que alcanzaría un clasificador supervisado normal.

La exactitud óptima se encuentra entre estos dos extremos, con un umbral de alrededor de 0.7.

print(__doc__)

# Authors: Oliver Rausch <rauscho@ethz.ch>
# License: BSD

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import StratifiedKFold
from sklearn.semi_supervised import SelfTrainingClassifier
from sklearn.metrics import accuracy_score
from sklearn.utils import shuffle

n_splits = 3

X, y = datasets.load_breast_cancer(return_X_y=True)
X, y = shuffle(X, y, random_state=42)
y_true = y.copy()
y[50:] = -1
total_samples = y.shape[0]

base_classifier = SVC(probability=True, gamma=0.001, random_state=42)

x_values = np.arange(0.4, 1.05, 0.05)
x_values = np.append(x_values, 0.99999)
scores = np.empty((x_values.shape[0], n_splits))
amount_labeled = np.empty((x_values.shape[0], n_splits))
amount_iterations = np.empty((x_values.shape[0], n_splits))

for (i, threshold) in enumerate(x_values):
    self_training_clf = SelfTrainingClassifier(base_classifier,
                                               threshold=threshold)

    # We need manual cross validation so that we don't treat -1 as a separate
    # class when computing accuracy
    skfolds = StratifiedKFold(n_splits=n_splits)
    for fold, (train_index, test_index) in enumerate(skfolds.split(X, y)):
        X_train = X[train_index]
        y_train = y[train_index]
        X_test = X[test_index]
        y_test = y[test_index]
        y_test_true = y_true[test_index]

        self_training_clf.fit(X_train, y_train)

        # The amount of labeled samples that at the end of fitting
        amount_labeled[i, fold] = total_samples - np.unique(
            self_training_clf.labeled_iter_, return_counts=True)[1][0]
        # The last iteration the classifier labeled a sample in
        amount_iterations[i, fold] = np.max(self_training_clf.labeled_iter_)

        y_pred = self_training_clf.predict(X_test)
        scores[i, fold] = accuracy_score(y_test_true, y_pred)


ax1 = plt.subplot(211)
ax1.errorbar(x_values, scores.mean(axis=1),
             yerr=scores.std(axis=1),
             capsize=2, color='b')
ax1.set_ylabel('Accuracy', color='b')
ax1.tick_params('y', colors='b')

ax2 = ax1.twinx()
ax2.errorbar(x_values, amount_labeled.mean(axis=1),
             yerr=amount_labeled.std(axis=1),
             capsize=2, color='g')
ax2.set_ylim(bottom=0)
ax2.set_ylabel('Amount of labeled samples', color='g')
ax2.tick_params('y', colors='g')

ax3 = plt.subplot(212, sharex=ax1)
ax3.errorbar(x_values, amount_iterations.mean(axis=1),
             yerr=amount_iterations.std(axis=1),
             capsize=2, color='b')
ax3.set_ylim(bottom=0)
ax3.set_ylabel('Amount of iterations')
ax3.set_xlabel('Threshold')

plt.show()