Nota
Haz clic aquí para descargar el código completo del ejemplo o para ejecutar este ejemplo en tu navegador a través de Binder
Precisión-Exhaustividad¶
Ejemplo de la métrica Precisión-Exhaustividad(Precision-recall) para evaluar la calidad del resultado del clasificador.
La precisión-exhaustividad es una medida útil del éxito de la predicción cuando las clases están muy desequilibradas. En la recuperación de información, la precisión es una medida de la relevancia de los resultados, mientras que la exhaustibidad es una medida de cuántos resultados realmente relevantes se devuelven.
La curva de precisión-exhaustividad muestra el equilibrio entre la precisión y la exhaustividad para diferentes umbrales. Un área alta bajo la curva representa tanto una alta exhaustividad como una alta precisión, donde una alta precisión se relaciona con una baja tasa de falsos positivos, y una alta exhaustividad se relaciona con una baja tasa de falsos negativos. Unas puntuaciones altas en ambos casos indican que el clasificador está devolviendo resultados exactos (alta precisión), además de devolver la mayoría de los resultados positivos (alta exhaustividad).
Un sistema con un alto grado de exhaustividad pero una baja precisión devuelve muchos resultados, pero la mayoría de sus etiquetas predichas son incorrectas cuando se comparan con las etiquetas de entrenamiento. Un sistema con alta precisión pero baja exhaustividad es justo lo contrario, ya que devuelve muy pocos resultados, pero la mayoría de sus etiquetas predichas son correctas cuando se comparan con las etiquetas de entrenamiento. Un sistema ideal con alta precisión y alta exhaustividad devolverá muchos resultados, con todos los resultados etiquetados correctamente.
La precisión (\(P\)) se define como el número de verdaderos positivos (\(T_p\)) sobre el número de verdaderos positivos más el número de falsos positivos (\(F_p\)).
\(P = \frac{T_p}{T_p+F_p}\)
La exhaustividad (\(R\)) se define como el número de verdaderos positivos (\(T_p\)) sobre el número de verdaderos positivos más el número de falsos negativos (\(F_n\)).
\(R = \frac{T_p}{T_p + F_n}\)
Estas cantidades también están relacionadas con la puntuación (\(F_1\)), que se define como la media armónica de la precisión y la exhaustividad.
\(F1 = 2\frac{P \times R}{P+R}\)
Ten en cuenta que la precisión puede no disminuir con la exhaustividad. La definición de precisión (\(\frac{T_p}{T_p + F_p}\)) muestra que la reducción del umbral de un clasificador puede aumentar el denominador, al aumentar el número de resultados devueltos. Si el umbral era demasiado alto, los nuevos resultados pueden ser todos verdaderos positivos, lo que aumentará la precisión. Si el umbral anterior era más o menos correcto o demasiado bajo, si se sigue bajando el umbral se introducirán falsos positivos, lo que disminuirá la precisión.
La exhaustividad se define como \(frac{T_p}{T_p+F_n}\), donde \(T_p+F_n\) no depende del umbral del clasificador. Esto significa que reducir el umbral del clasificador puede aumentar la recuperación, al aumentar el número de resultados verdaderos positivos. También es posible que la reducción del umbral deje la exhaustividad sin cambios, mientras que la precisión fluctúa.
La relación entre la exhaustividad y la precisión puede observarse en la zona de los escalones del gráfico: en los bordes de estos escalones, un pequeño cambio en el umbral reduce considerablemente la precisión, con sólo una pequeña ganancia en la exhaustividad.
La precisión media (Average precision, AP) resume dicho gráfico como la media ponderada de las precisiones alcanzadas en cada umbral, utilizando como ponderación el aumento de la exhaustividad desde el umbral anterior:
\(\text{AP} = \sum_n (R_n - R_{n-1}) P_n\)
donde \(P_n\) y \(R_n\) son la precisión y la exhaustividad en el enésimo umbral. Un par \((R_k, P_k)\) se denomina punto de operación.
AP y el área trapezoidal bajo los puntos de operación (sklearn.metrics.auc) son formas comunes de resumir una curva de precisión-exhaustividad que conducen a diferentes resultados. Lee más en el Manual del usuario.
Las curvas de precisión-exhaustividad se utilizan normalmente en la clasificación binaria para estudiar el resultado de un clasificador. Para ampliar la curva de precisión-exhaustividad y la precisión media a la clasificación multiclase o multietiqueta, es necesario binarizar el resultado. Se puede dibujar una curva por etiqueta, pero también se puede dibujar una curva de precisión-exhaustividad considerando cada elemento de la matriz de indicatriz de etiquetas como una predicción binaria (micropromedio).
Nota
En configuraciones de clasificación binaria¶
Crea datos simples¶
Intenta diferenciar las dos primeras clases de los datos iris
from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
import numpy as np
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Add noisy features
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]
# Limit to the two first classes, and split into training and test
X_train, X_test, y_train, y_test = train_test_split(X[y < 2], y[y < 2],
test_size=.5,
random_state=random_state)
# Create a simple classifier
classifier = svm.LinearSVC(random_state=random_state)
classifier.fit(X_train, y_train)
y_score = classifier.decision_function(X_test)
Calcula la puntuación media de precisión¶
from sklearn.metrics import average_precision_score
average_precision = average_precision_score(y_test, y_score)
print('Average precision-recall score: {0:0.2f}'.format(
average_precision))
Out:
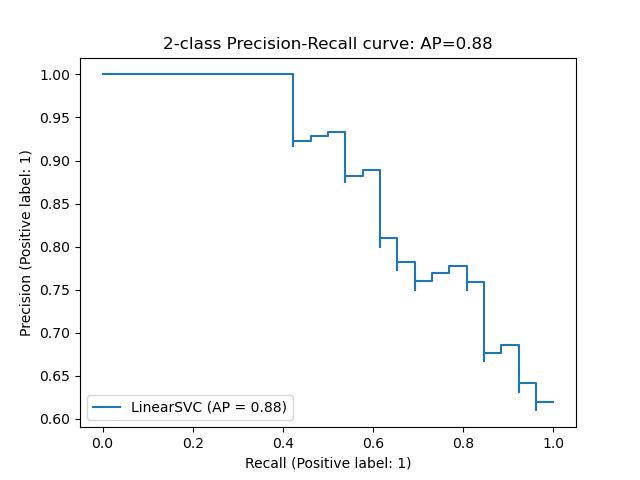
Average precision-recall score: 0.88
Grafica la curva de Precisión-Exhaustividad¶
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import plot_precision_recall_curve
import matplotlib.pyplot as plt
disp = plot_precision_recall_curve(classifier, X_test, y_test)
disp.ax_.set_title('2-class Precision-Recall curve: '
'AP={0:0.2f}'.format(average_precision))
Out:
Text(0.5, 1.0, '2-class Precision-Recall curve: AP=0.88')
En configuraciones multietiqueta¶
Crea datos multietiqueta, ajusta y predice¶
Creamos un conjunto de datos multietiqueta, para ilustrar la precisión-exhaustividad en configuraciones multietiqueta
from sklearn.preprocessing import label_binarize
# Use label_binarize to be multi-label like settings
Y = label_binarize(y, classes=[0, 1, 2])
n_classes = Y.shape[1]
# Split into training and test
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.5,
random_state=random_state)
# We use OneVsRestClassifier for multi-label prediction
from sklearn.multiclass import OneVsRestClassifier
# Run classifier
classifier = OneVsRestClassifier(svm.LinearSVC(random_state=random_state))
classifier.fit(X_train, Y_train)
y_score = classifier.decision_function(X_test)
La puntuación media de la precisión en configuraciones multietiqueta¶
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score
# For each class
precision = dict()
recall = dict()
average_precision = dict()
for i in range(n_classes):
precision[i], recall[i], _ = precision_recall_curve(Y_test[:, i],
y_score[:, i])
average_precision[i] = average_precision_score(Y_test[:, i], y_score[:, i])
# A "micro-average": quantifying score on all classes jointly
precision["micro"], recall["micro"], _ = precision_recall_curve(Y_test.ravel(),
y_score.ravel())
average_precision["micro"] = average_precision_score(Y_test, y_score,
average="micro")
print('Average precision score, micro-averaged over all classes: {0:0.2f}'
.format(average_precision["micro"]))
Out:
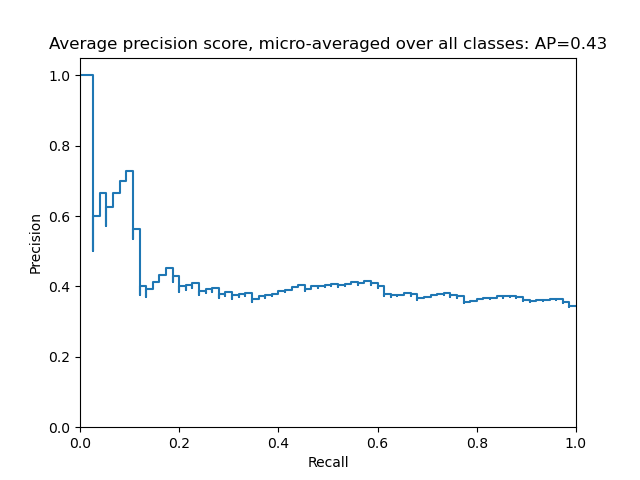
Average precision score, micro-averaged over all classes: 0.43
Grafica la curva de precisión-exhaustividad micropromediada¶
plt.figure()
plt.step(recall['micro'], precision['micro'], where='post')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title(
'Average precision score, micro-averaged over all classes: AP={0:0.2f}'
.format(average_precision["micro"]))
Out:
Text(0.5, 1.0, 'Average precision score, micro-averaged over all classes: AP=0.43')
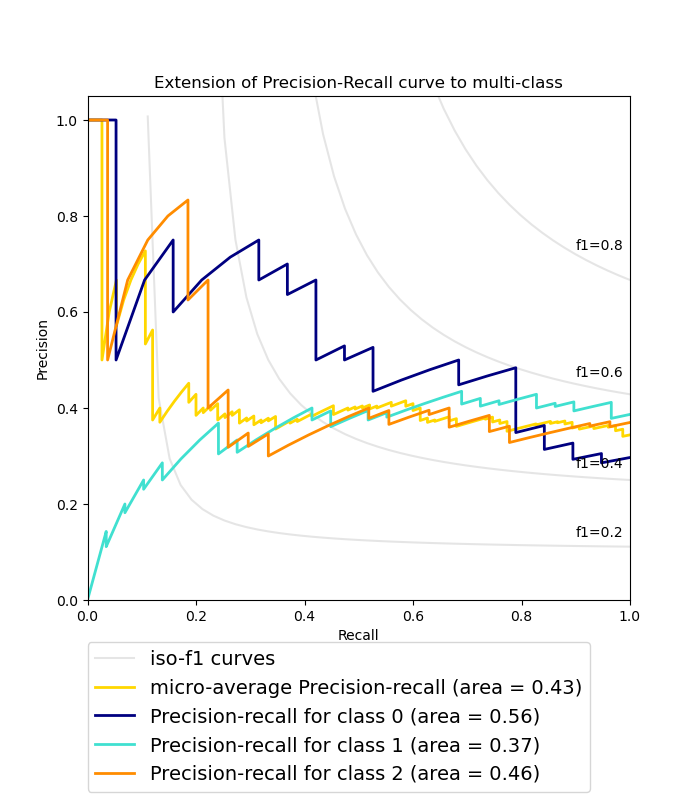
Grafica la curva de Precisión-Exhaustividad para cada clase y las curvas iso-f1¶
from itertools import cycle
# setup plot details
colors = cycle(['navy', 'turquoise', 'darkorange', 'cornflowerblue', 'teal'])
plt.figure(figsize=(7, 8))
f_scores = np.linspace(0.2, 0.8, num=4)
lines = []
labels = []
for f_score in f_scores:
x = np.linspace(0.01, 1)
y = f_score * x / (2 * x - f_score)
l, = plt.plot(x[y >= 0], y[y >= 0], color='gray', alpha=0.2)
plt.annotate('f1={0:0.1f}'.format(f_score), xy=(0.9, y[45] + 0.02))
lines.append(l)
labels.append('iso-f1 curves')
l, = plt.plot(recall["micro"], precision["micro"], color='gold', lw=2)
lines.append(l)
labels.append('micro-average Precision-recall (area = {0:0.2f})'
''.format(average_precision["micro"]))
for i, color in zip(range(n_classes), colors):
l, = plt.plot(recall[i], precision[i], color=color, lw=2)
lines.append(l)
labels.append('Precision-recall for class {0} (area = {1:0.2f})'
''.format(i, average_precision[i]))
fig = plt.gcf()
fig.subplots_adjust(bottom=0.25)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Extension of Precision-Recall curve to multi-class')
plt.legend(lines, labels, loc=(0, -.38), prop=dict(size=14))
plt.show()
Tiempo total de ejecución del script: (0 minutos 0.596 segundos)
