FastICA en nubes de puntos 2D

Este ejemplo ilustra visualmente en el espacio de características una comparación por resultados utilizando dos técnicas diferentes de análisis de componentes.

Análisis de componentes independientes (ICA) vs Análisis de componentes principales (PCA).

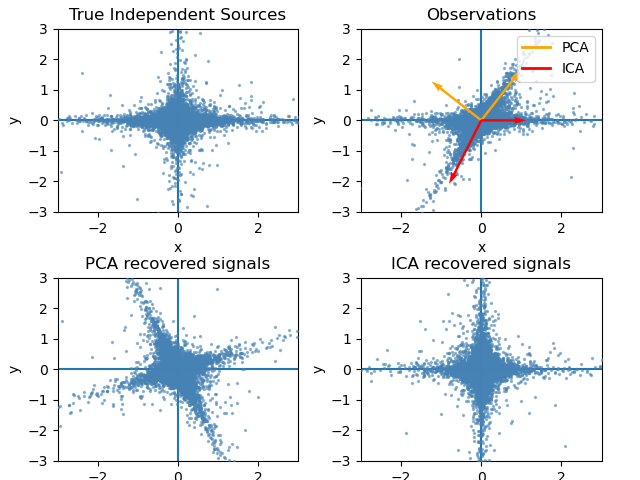
La representación de ICA en el espacio de características da la visión de “ICA geométrico”: El ICA es un algoritmo que encuentra direcciones en el espacio de características correspondientes a proyecciones con alta no gaussianidad. Estas direcciones no tienen por qué ser ortogonales en el espacio de características original, pero son ortogonales en el espacio de características blanqueado, en el que todas las direcciones corresponden a la misma varianza.

El PCA, por su parte, encuentra direcciones ortogonales en el espacio de características en bruto que corresponden a direcciones que representan la máxima varianza.

Aquí simulamos fuentes independientes utilizando un proceso altamente no gaussiano, 2 estudiantes T con un bajo número de grados de libertad (figura superior izquierda). Las mezclamos para crear observaciones (figura superior derecha). En este espacio de observación en bruto, las direcciones identificadas por el PCA se representan con vectores de color naranja. Representamos la señal en el espacio PCA, después de blanquearla por la varianza correspondiente a los vectores PCA (parte inferior izquierda). Ejecutar el ICA corresponde a encontrar una rotación en este espacio para identificar las direcciones de mayor no gaussianidad (abajo a la derecha).

print(__doc__)

# Authors: Alexandre Gramfort, Gael Varoquaux
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.decomposition import PCA, FastICA

# #############################################################################
# Generate sample data
rng = np.random.RandomState(42)
S = rng.standard_t(1.5, size=(20000, 2))
S[:, 0] *= 2.

# Mix data
A = np.array([[1, 1], [0, 2]])  # Mixing matrix

X = np.dot(S, A.T)  # Generate observations

pca = PCA()
S_pca_ = pca.fit(X).transform(X)

ica = FastICA(random_state=rng)
S_ica_ = ica.fit(X).transform(X)  # Estimate the sources

S_ica_ /= S_ica_.std(axis=0)


# #############################################################################
# Plot results

def plot_samples(S, axis_list=None):
    plt.scatter(S[:, 0], S[:, 1], s=2, marker='o', zorder=10,
                color='steelblue', alpha=0.5)
    if axis_list is not None:
        colors = ['orange', 'red']
        for color, axis in zip(colors, axis_list):
            axis /= axis.std()
            x_axis, y_axis = axis
            # Trick to get legend to work
            plt.plot(0.1 * x_axis, 0.1 * y_axis, linewidth=2, color=color)
            plt.quiver((0, 0), (0, 0), x_axis, y_axis, zorder=11, width=0.01,
                       scale=6, color=color)

    plt.hlines(0, -3, 3)
    plt.vlines(0, -3, 3)
    plt.xlim(-3, 3)
    plt.ylim(-3, 3)
    plt.xlabel('x')
    plt.ylabel('y')

plt.figure()
plt.subplot(2, 2, 1)
plot_samples(S / S.std())
plt.title('True Independent Sources')

axis_list = [pca.components_.T, ica.mixing_]
plt.subplot(2, 2, 2)
plot_samples(X / np.std(X), axis_list=axis_list)
legend = plt.legend(['PCA', 'ICA'], loc='upper right')
legend.set_zorder(100)

plt.title('Observations')

plt.subplot(2, 2, 3)
plot_samples(S_pca_ / np.std(S_pca_, axis=0))
plt.title('PCA recovered signals')

plt.subplot(2, 2, 4)
plot_samples(S_ica_ / np.std(S_ica_))
plt.title('ICA recovered signals')

plt.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.36)
plt.show()