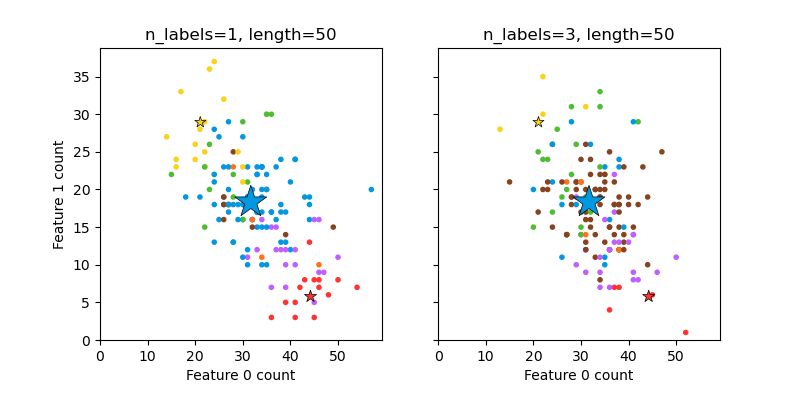
Graficar el conjunto de datos multietiqueta generados aleatoriamente

Esto ilustra el generador de conjuntos de datos make_multilabel_classification. Cada muestra consta de recuentos de dos características (hasta 50 en total), que se distribuyen de forma diferente en cada una de las dos clases.

Los puntos se etiquetan de la siguiente manera, donde Y significa que la clase está presente:

1	2	3	Color
Y	N	N	Rojo
N	Y	N	Azul
N	N	Y	Amarillo
Y	Y	N	Púrpura
Y	N	Y	Naranja
Y	Y	N	Verde
Y	Y	Y	Marrón

Una estrella marca la muestra esperada para cada clase; su tamaño refleja la probabilidad de seleccionar esa etiqueta de clase.

Los ejemplos de la izquierda y la derecha destacan el parámetro n_labels: un mayor número de muestras en el gráfico de la derecha tiene 2 o 3 etiquetas.

Ten en cuenta que este ejemplo bidimensional es muy degenerado: generalmente el número de características sería mucho mayor que la «longitud del documento», mientras que aquí tenemos documentos mucho más grandes que el vocabulario. Del mismo modo, con n_classes > n_features, es mucho menos probable que una característica distinga una clase particular.

Out:

The data was generated from (random_state=511):
Class   P(C)    P(w0|C) P(w1|C)
red     0.20    0.88    0.12
blue    0.61    0.63    0.37
yellow  0.18    0.42    0.58

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import make_multilabel_classification as make_ml_clf

print(__doc__)

COLORS = np.array(['!',
                   '#FF3333',  # red
                   '#0198E1',  # blue
                   '#BF5FFF',  # purple
                   '#FCD116',  # yellow
                   '#FF7216',  # orange
                   '#4DBD33',  # green
                   '#87421F'   # brown
                   ])

# Use same random seed for multiple calls to make_multilabel_classification to
# ensure same distributions
RANDOM_SEED = np.random.randint(2 ** 10)


def plot_2d(ax, n_labels=1, n_classes=3, length=50):
    X, Y, p_c, p_w_c = make_ml_clf(n_samples=150, n_features=2,
                                   n_classes=n_classes, n_labels=n_labels,
                                   length=length, allow_unlabeled=False,
                                   return_distributions=True,
                                   random_state=RANDOM_SEED)

    ax.scatter(X[:, 0], X[:, 1], color=COLORS.take((Y * [1, 2, 4]
                                                    ).sum(axis=1)),
               marker='.')
    ax.scatter(p_w_c[0] * length, p_w_c[1] * length,
               marker='*', linewidth=.5, edgecolor='black',
               s=20 + 1500 * p_c ** 2,
               color=COLORS.take([1, 2, 4]))
    ax.set_xlabel('Feature 0 count')
    return p_c, p_w_c


_, (ax1, ax2) = plt.subplots(1, 2, sharex='row', sharey='row', figsize=(8, 4))
plt.subplots_adjust(bottom=.15)

p_c, p_w_c = plot_2d(ax1, n_labels=1)
ax1.set_title('n_labels=1, length=50')
ax1.set_ylabel('Feature 1 count')

plot_2d(ax2, n_labels=3)
ax2.set_title('n_labels=3, length=50')
ax2.set_xlim(left=0, auto=True)
ax2.set_ylim(bottom=0, auto=True)

plt.show()

print('The data was generated from (random_state=%d):' % RANDOM_SEED)
print('Class', 'P(C)', 'P(w0|C)', 'P(w1|C)', sep='\t')
for k, p, p_w in zip(['red', 'blue', 'yellow'], p_c, p_w_c.T):
    print('%s\t%0.2f\t%0.2f\t%0.2f' % (k, p, p_w[0], p_w[1]))